

所属成套资源:全国通用 中考数学 二次函数压轴题专题练习
全国通用 中考数学 二次函数压轴题专题练习 12直角三角形存在性问题(不含答案版)
展开这是一份全国通用 中考数学 二次函数压轴题专题练习 12直角三角形存在性问题(不含答案版),共8页。
一、几何法:两线一圆得坐标
(1)若∠A为直角,过点A作AB的垂线,与x轴的交点即为所求点C;
(2)若∠B为直角,过点B作AB的垂线,与x轴的交点即为所求点C;
(3)若∠C为直角,以AB为直径作圆,与x轴的交点即为所求点C.(直径所对的圆周角为直角)
二、构造三垂直:
构造三垂直步骤:
①过直角顶点作一条水平或竖直的直线;
②过另外两端点向该直线作垂线,即可得三垂直相似.
三、代数法:表示线段构勾股
(1)表示点:设坐标为(m,0),又A(1,1)、B(5,3);
(2)表示线段:,,;
(3)分类讨论:当为直角时,;
(4)代入得方程:,解得:.
小结:
几何法:(1)“两线一圆”作出点;
(2)构造三垂直相似,利用对应边成比例求线段,必要时可设未知数.
代数法:(1)表示点A、B、C坐标;
(2)表示线段AB、AC、BC;
(3)分类讨论①AB²+AC²=BC²、②AB²+BC²=AC²、③AC²+BC²=AB²;
(4)代入列方程,求解.
如果问题变为等腰直角三角形存在性,则同样可采取上述方法,只不过三垂直得到的不是相似,而是全等.
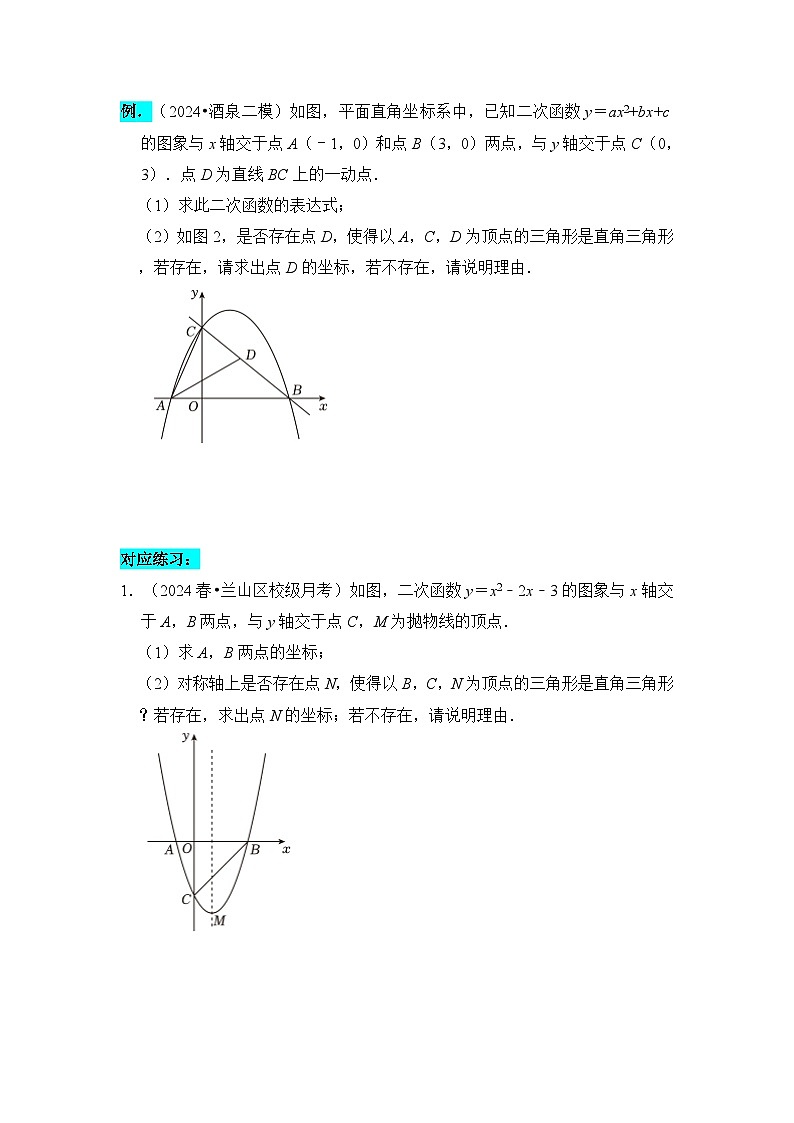
例.(2024•酒泉二模)如图,平面直角坐标系中,已知二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)和点B(3,0)两点,与y轴交于点C(0,3).点D为直线BC上的一动点.
(1)求此二次函数的表达式;
(2)如图2,是否存在点D,使得以A,C,D为顶点的三角形是直角三角形,若存在,请求出点D的坐标,若不存在,请说明理由.
对应练习:
1.(2024春•兰山区校级月考)如图,二次函数y=x2﹣2x﹣3的图象与x轴交于A,B两点,与y轴交于点C,M为抛物线的顶点.
(1)求A,B两点的坐标;
(2)对称轴上是否存在点N,使得以B,C,N为顶点的三角形是直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
2.(2024•富顺县二模)在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
(1)求二次函数的解析式;
(2)在二次函数y=x2+bx+c的图象上是否存在点M,使三角形ACM是以AC为直角边的直角三角形.若存在,求出点M的坐标;若不存在,请说明理由.
3.(2024•秭归县模拟)在平面直角坐标系中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线L1:交x轴于点A,B(点A在点B左侧),交y轴于点C.抛物线L2与L1是“共根抛物线”,其顶点为P.
(1)若抛物线L2经过点(1,﹣5),求抛物线L2对应的函数关系式;
(2)是否存在以点A,C,P为顶点的三角形是以AC为直角边的直角三角形?若存在,求出抛物线L2对应的函数关系式;若不存在,请说明理由.
4.(2024•遂宁)二次函数y=ax2+bx+c(a≠0)的图象与x轴分别交于点A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3),P、Q为抛物线上的两点.
(1)求二次函数的表达式;
(2)当P、C两点关于抛物线对称轴对称,△OPQ是以点P为直角顶点的直角三角形时,求点Q的坐标;
5.(2024•锦江区校级模拟)如图,二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0),B(4,0),C(0,2),连接线段AC和线段BC.
(1)求这个二次函数的解析式.
(2)若动点E从A点出发以每秒1个单位长度的速度向点B运动;同时,动点F从点B出发以每秒个单位长度的速度向点C运动,当一个点到达终点时,另一个点停止运动,设动点运动时间为t秒,求当t为何值时,△BEF为直角三角形.
6.(2024春•威远县校级期中)已知:二次函数y=x2+bx+c的顶点P在直线y=﹣4x上,并且图象经过点A(﹣1,0).
(1)求这个二次函数的解析式;
(2)D是线段BP上的一个动点,过点D作DE⊥x轴于点E,E点的坐标为(a,0).在BP上是否存在点D,使△DCE为直角三角形?若存在,请求出点D的坐标,若不存在,请说明理由.
7.(2023秋•新会区校级月考)如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2).
(1)求二次函数的解析式;
(2)二次函数的对称轴上是否存在点P,使△PBC是直角三角形?如果存在,请直接写出答案,如果不存在,请说明理由.
8.(2024•凉州区二模)如图,已知:关于y的二次函数y=x2+bx+c的图象与x轴交于点A(2,0)和点B,与y轴交于点C(0,6),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式.
(2)在y轴上是否存在一点P,使△PBC为直角三角形.若存在,请求出点P的坐标.
9.(2023秋•伊通县校级月考)如图①,二次函数y=x2﹣4x﹣5与x轴交于点A、C,且点A在点C的右侧,与y轴交于点B,连接AB.
(1)求抛物线的对称轴;
(2)求直线AB的解析式;
(3)如图②,点P是x轴下方、抛物线对称轴右侧图象上的一动点,连接PB,过点P作PQ∥AB,与抛物线的另一个交点为Q,M、N为AB上的两点,且PM∥y轴,QN∥y轴.
①当△BPM为直角三角形时,求点P的坐标;
10.(2024•娄底模拟)如图,抛物线C:y=ax2+6ax+9a﹣8与x轴相交于A,B两点(点A在点B的左侧),已知点B的横坐标是2,抛物线C的顶点为D.
(1)求a的值及顶点D的坐标;
(2)点P是x轴正半轴上一点,将抛物线C绕点P旋转180°后得到抛物线C1,记抛物线C1的顶点为E,抛物线C1与x轴的交点为F,G(点F在点G的右侧).当点P与点B重合时(如图1),求抛物线C1的表达式;
(3)如图2,在(2)的条件下,从A,B,D中任取一点,E,F,G中任取两点,若以取出的三点为顶点能构成直角三角形,我们就称抛物线C1为抛物线C的“勾股伴随同类函数”.当抛物线C1是抛物线C的勾股伴随同类函数时,求点P的坐标.
相关试卷
这是一份全国通用 中考数学 二次函数压轴题专题练习 13等腰直角三角形存在性问题(不含答案版),共7页。试卷主要包含了综合与探究,是抛物线上的动点,是抛物线上的一个动点等内容,欢迎下载使用。
这是一份全国通用 中考数学 二次函数压轴题专题练习 12直角三角形存在性问题(含答案解析版),共19页。
这是一份全国通用 中考数学 二次函数压轴题专题练习 10正方形存在性问题(不含答案版),共7页。试卷主要包含了【实践探究】,综合与探究等内容,欢迎下载使用。












