全国通用 中考数学 二次函数压轴题专题练习 13等腰直角三角形存在性问题（不含答案版）

这是一份全国通用 中考数学 二次函数压轴题专题练习 13等腰直角三角形存在性问题（不含答案版），共7页。试卷主要包含了综合与探究，是抛物线上的动点，是抛物线上的一个动点等内容，欢迎下载使用。
如图，抛物线y＝x2﹣3x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接BC．若点P在线段BC上运动（点P不与点B，C重合），过点P作x轴的垂线，交抛物线于点E，交x轴于点F．设点P的横坐标为m．
（1）求点A，B，C的坐标，并直接写出直线BC的函数解析式．
（2）在点P的运动过程中，是否存在m使得△CPE为等腰直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．
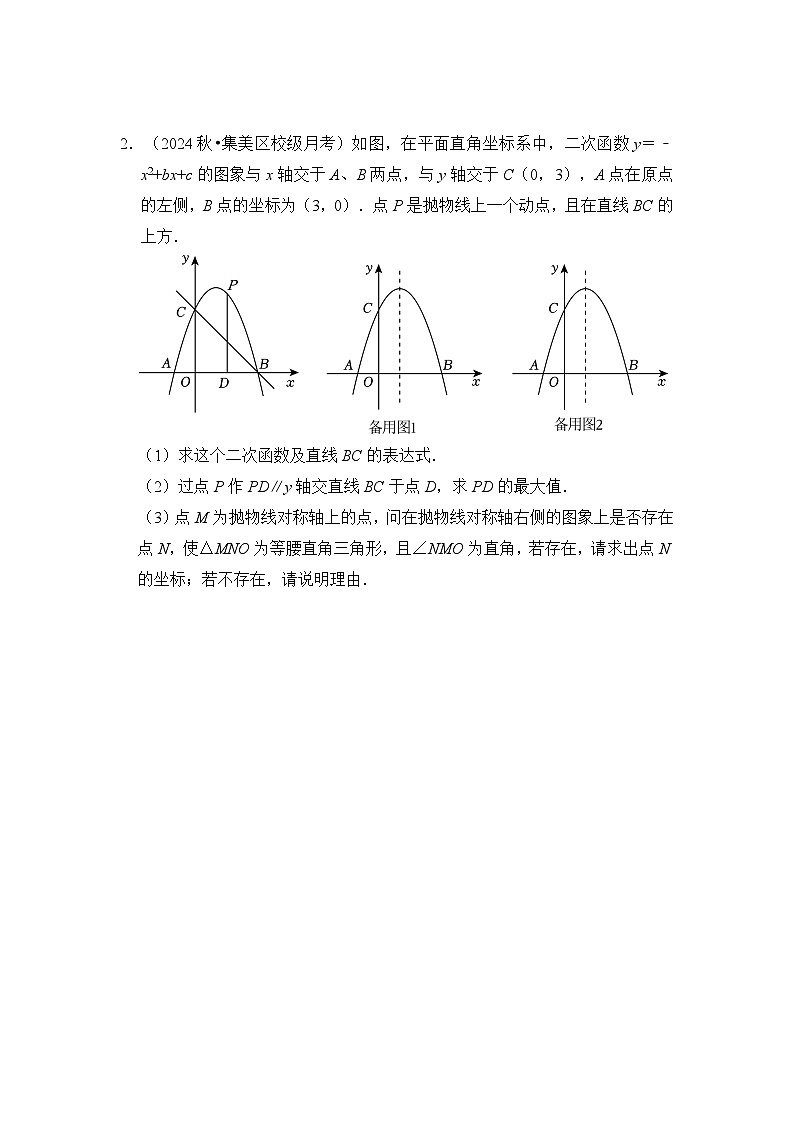
2．（2024秋•集美区校级月考）如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．
（1）求这个二次函数及直线BC的表达式．
（2）过点P作PD∥y轴交直线BC于点D，求PD的最大值．
（3）点M为抛物线对称轴上的点，问在抛物线对称轴右侧的图象上是否存在点N，使△MNO为等腰直角三角形，且∠NMO为直角，若存在，请求出点N的坐标；若不存在，请说明理由．
3．（2024秋•中山市校级月考）九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践—应用—探究的过程
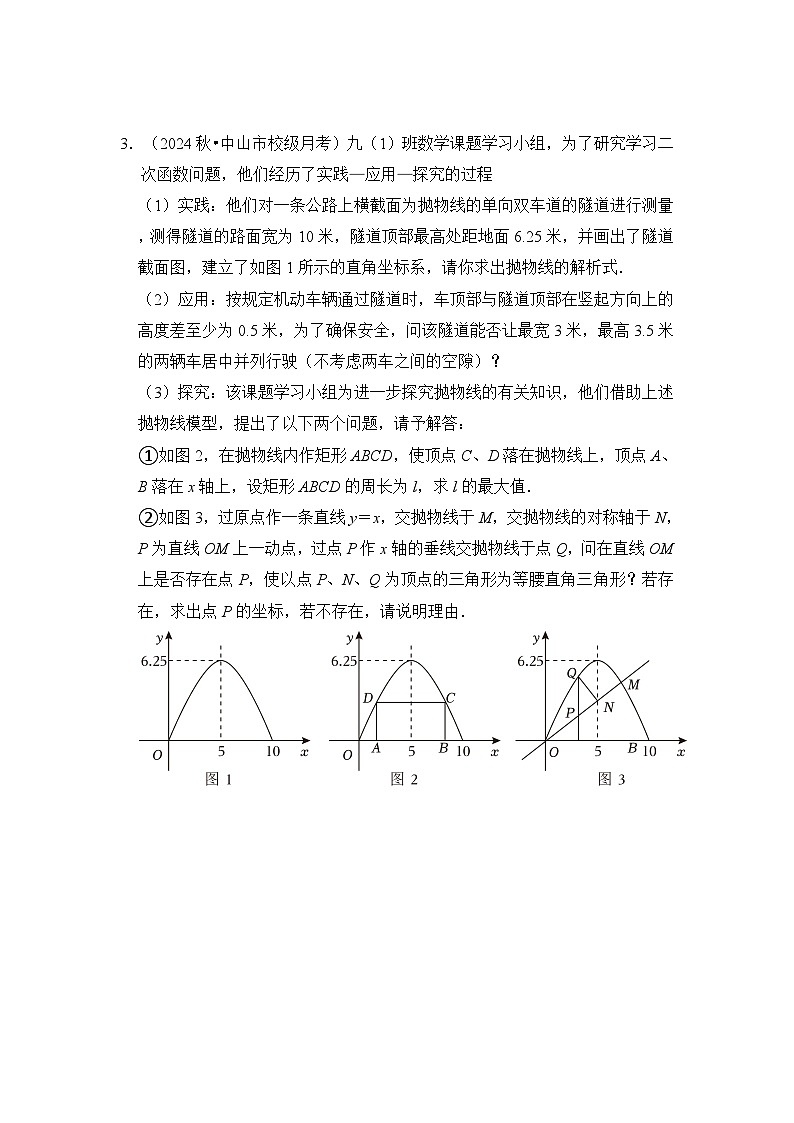
（1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量，测得隧道的路面宽为10米，隧道顶部最高处距地面6.25米，并画出了隧道截面图，建立了如图1所示的直角坐标系，请你求出抛物线的解析式．
（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖起方向上的高度差至少为0.5米，为了确保安全，问该隧道能否让最宽3米，最高3.5米的两辆车居中并列行驶（不考虑两车之间的空隙）？
（3）探究：该课题学习小组为进一步探究抛物线的有关知识，他们借助上述抛物线模型，提出了以下两个问题，请予解答：
①如图2，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上，设矩形ABCD的周长为l，求l的最大值．
②如图3，过原点作一条直线y＝x，交抛物线于M，交抛物线的对称轴于N，P为直线OM上一动点，过点P作x轴的垂线交抛物线于点Q，问在直线OM上是否存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．
4．（2024•海南模拟）如图1，抛物线与x轴交于A（﹣2，0），B（﹣8，0）两点，与y轴交于点C（0，﹣8）．经过点A的直线与抛物线交于另一点D，与y轴交于点E（0，1）．
（1）求该二次函数的解析式；
（2）连接AC、DC，求△ACD的面积；
（3）如图1，点P是线段AD上一动点，过点P作PF∥y轴，交该抛物线于点F，作FG∥x轴，交该抛物线于另一点G．
①若△PFG是等腰直角三角形，求PF的长；
②如图2，点P的横坐标为﹣6，点M是直线AD上方抛物线上的一个动点，点N是y轴负半轴上一动点．请问是否存在点M，使得以P、N、E为顶点的三角形与△PME全等，且以同一条线段PE为对应边？若存在，直接写出点M的坐标；若不存在，请说明理由．
5．（2024•文昌校级模拟）如图，二次函数y＝ax2﹣4x+c（a≠0）的图象与x轴交于点A、B（3，0），与y轴交于点C（0，3），点P（m，n）是抛物线上的动点．
（1）求抛物线的表达式；
（2）如图1，当m＝2时，求△BCP的面积；
（3）当∠PCB＝15°时，求点P的坐标；
（4）如图2，点Q是抛物线对称轴上一点，是否存在点P，使△POQ是以点P为直角顶点的等腰直角三角形，若存在，请直接写出m的值；若不存在，请说明理由．
6．（2024•东昌府区模拟）如图，抛物线y＝ax2+bx+c过x轴上点A（﹣1，0）、点B（5，0），过y轴上点C（0，﹣5），点P（m，n）（0＜m＜5）是抛物线上的一个动点．
（1）求该二次函数的表达式；
（2）求四边形OCPB面积的最大值；
（3）当点P的横坐标m满足2＜m＜5时，过点P作PE⊥x轴，交BC于点E，再过点P作PF∥x轴，交抛物线于点F，连接EF，求使△PEF为等腰直角三角形的点P的坐标．
7．（2023•阜新模拟）如图，在平面直角坐标系中，直线y＝x+4与x轴，y轴分别交于点A，C，抛物线y＝﹣x2+bx+c过点A和点C，与x轴交于点B．
（1）求这个二次函数的表达式；
（2）抛物线对称轴与直线AC交于点D，若P是直线AC上方抛物线上的一个动点（点P不与点A，C重合），求△PAD面积的最大值；
（3）点M是抛物线对称轴上的一动点，x轴上方的抛物线上是否存在点N，使得△ANM是以AN为直角边的等腰直角三角形；若存在，请直接写出点N坐标；若不存在，请说明理由．