全国通用 中考数学 二次函数压轴题专题练习 13等腰直角三角形存在性问题（含答案解析版）

这是一份全国通用 中考数学 二次函数压轴题专题练习 13等腰直角三角形存在性问题（含答案解析版），共20页。试卷主要包含了综合与探究，是抛物线上的动点，是抛物线上的一个动点等内容，欢迎下载使用。
如图，抛物线y＝x2﹣3x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接BC．若点P在线段BC上运动（点P不与点B，C重合），过点P作x轴的垂线，交抛物线于点E，交x轴于点F．设点P的横坐标为m．
（1）求点A，B，C的坐标，并直接写出直线BC的函数解析式．
（2）在点P的运动过程中，是否存在m使得△CPE为等腰直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．
【解答】解：（1）当y＝0时，x2﹣3x﹣4＝0，
解得x＝4或x＝﹣1，
∴A（﹣1，0），B（4，0），
当x＝0时，y＝﹣4，
∴C（0，﹣4），
设直线BC的解析式为y＝kx﹣4，
将点B代入可得4k﹣4＝0，
解得k＝1，
∴直线BC的解析式为y＝x﹣4；
（2）存在m使得△CPE为等腰直角三角形，理由如下：
由（2）可得，PC2＝2m2，PE2＝（m2+4m）2，CE2＝m2+（m2﹣3m）2，
当∠PCE＝90°时，PE2＝2PC2，即（m2+4m）2＝4m2，
解得m＝2或m＝6（舍）；
当∠CEP＝90°时，2CE2＝PC2，即2m2+2（m2﹣3m）2＝2m2，
解得m＝3或m＝5（舍）；
综上所述：m的值为3或2．
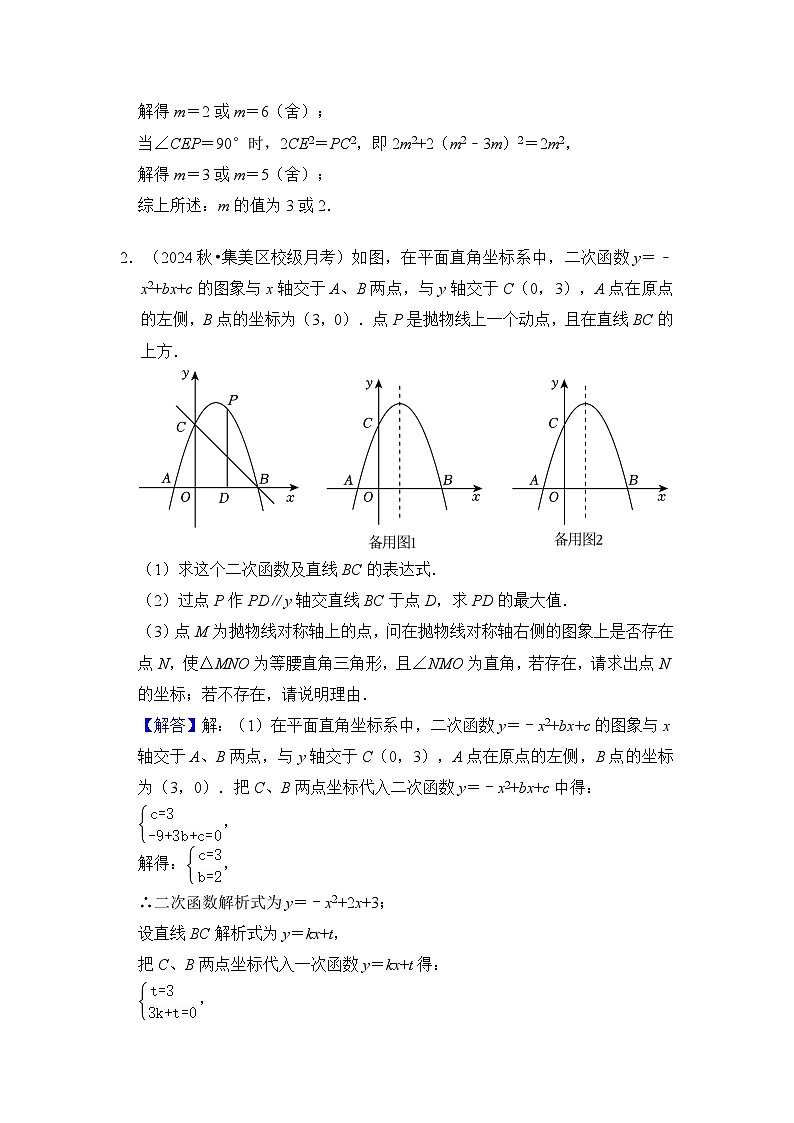
2．（2024秋•集美区校级月考）如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．
（1）求这个二次函数及直线BC的表达式．
（2）过点P作PD∥y轴交直线BC于点D，求PD的最大值．
（3）点M为抛物线对称轴上的点，问在抛物线对称轴右侧的图象上是否存在点N，使△MNO为等腰直角三角形，且∠NMO为直角，若存在，请求出点N的坐标；若不存在，请说明理由．
【解答】解：（1）在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．把C、B两点坐标代入二次函数y＝﹣x2+bx+c中得：
，
解得：，
∴二次函数解析式为y＝﹣x2+2x+3；
设直线BC解析式为y＝kx+t，
把C、B两点坐标代入一次函数y＝kx+t得：
，
解得：，
∴直线BC解析式为y＝﹣x+3；
（2）∵点P在抛物线上，
∴设P（m，﹣m2+2m+3）；
∵PD∥y轴，
∴D（m，﹣m+3），
∴PD＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，
∵，且二次项系数﹣1＜0，
∴当时，PD有最大值；
（3）①当点M位于x轴上方时，
如图1，过N点作NG垂直对称轴于点G，设抛物线对称轴交x轴于点F；
则∠MFO＝∠NGM＝90°，
∵△MNO为等腰直角三角形，且∠NMO＝90°，
∴NM＝MO，∠NMO＝90°，
∴∠NMG+∠OMF＝90°，
∵∠NMG+∠MNG＝90°，
∴∠MNG＝∠OMF，
在△MGN和△OFM中，
，
∴△MGN≌△OFM（AAS），
∴OF＝GM，MF＝NG，
∵抛物线的对称轴为直线x＝1，
∴OF＝GM＝1；
设点M坐标为（1，a），此时a＞0，则NG＝MF＝a，
∴N（1+a，a﹣1）；
∵N点在抛物线上，
∴a﹣1＝﹣（1+a）2+2（a+1）+3，
解得：（舍去）；
∴N点坐标为；
当点M位于x轴下方时，此时a＜0；
同理得N（﹣a+1，a+1），
则有a+1＝﹣（﹣a+1）2+2（﹣a+1）+3，
解得：（舍去）；
∴N点坐标为；
综上，N点坐标为或．
3．（2024秋•中山市校级月考）九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践—应用—探究的过程
（1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量，测得隧道的路面宽为10米，隧道顶部最高处距地面6.25米，并画出了隧道截面图，建立了如图1所示的直角坐标系，请你求出抛物线的解析式．
（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖起方向上的高度差至少为0.5米，为了确保安全，问该隧道能否让最宽3米，最高3.5米的两辆车居中并列行驶（不考虑两车之间的空隙）？
（3）探究：该课题学习小组为进一步探究抛物线的有关知识，他们借助上述抛物线模型，提出了以下两个问题，请予解答：
①如图2，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上，设矩形ABCD的周长为l，求l的最大值．
②如图3，过原点作一条直线y＝x，交抛物线于M，交抛物线的对称轴于N，P为直线OM上一动点，过点P作x轴的垂线交抛物线于点Q，问在直线OM上是否存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．
【解答】解：（1）根据坐标系可知此函数顶点坐标为（5，6.25），且图象过（10，0）点，
代入顶点式得：y＝a（x﹣5）2+6.25，
∴0＝a（10﹣5）2+6.25，
解得：a＝﹣0.25，
∴y＝﹣0.25（x﹣5）2+6.25；
（2）当最宽3米，最高3.5米的两辆厢式货车居中并列行驶时，
∴10﹣3×2＝4，4÷2＝2，
∴x＝2代入解析式得：
y＝﹣0.25（2﹣5）2+6.25；
解得y＝4，
∴4﹣3.5＝0.5（米），
∴隧道能让最宽3米，最高3.5米的两辆厢式货车居中并列行驶；
（3）①假设AO＝x米，可得AB＝（10﹣2x）米，
∴AD＝﹣0.25（x﹣5）2+6.25（米）；
∵矩形ABCD的周长为l，
∴l＝2[﹣0.25（x﹣5）2+6.25]+2（10﹣2x）＝﹣0.5x2+x+20，
∴l的最大值为：；
②在直线OM上存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形；理由如下：
当以P、N、Q为顶点的三角形是等腰直角三角形时，
∵P在y＝x的图象上，过P点作x轴的垂线交抛物线于点Q．如图3，
∴∠POA＝∠OPA＝45°，
∴Q点的纵坐标为5，
∴5＝﹣m2+10m 4，
解得：，
∴P或，
当∠P3NQ3＝90°时，过点Q3作Q3K1⊥对称轴，
当△NQ3K1为等腰直角三角形时，△NP3Q3为等腰直角三角形，
Q点在OM的上方时，
P3Q3＝2Q3K1，P3Q3＝，Q3K1＝5﹣x，
Q点在OM的下方时，
P4Q4＝2Q4K2，P4Q4＝，Q4K2＝x﹣5，
∴，
解得：x1＝4，x2＝10，
P3（4，4），P4（10，10），
∴使以P、N、Q为顶点的三角形是等腰直角三角形，P点的坐标为：
或或（4，4）或（10，10）．
4．（2024•海南模拟）如图1，抛物线与x轴交于A（﹣2，0），B（﹣8，0）两点，与y轴交于点C（0，﹣8）．经过点A的直线与抛物线交于另一点D，与y轴交于点E（0，1）．
（1）求该二次函数的解析式；
（2）连接AC、DC，求△ACD的面积；
（3）如图1，点P是线段AD上一动点，过点P作PF∥y轴，交该抛物线于点F，作FG∥x轴，交该抛物线于另一点G．
①若△PFG是等腰直角三角形，求PF的长；
②如图2，点P的横坐标为﹣6，点M是直线AD上方抛物线上的一个动点，点N是y轴负半轴上一动点．请问是否存在点M，使得以P、N、E为顶点的三角形与△PME全等，且以同一条线段PE为对应边？若存在，直接写出点M的坐标；若不存在，请说明理由．
【解答】解：（1）设抛物线的解析式为y＝a（x+2）（x+8），
∴﹣8＝a•2×8，
∴a＝﹣，
∴y＝﹣；
（2）如图1，
作DQ⊥x轴于Q，
设D（m，﹣ （m+2）（m+8）），
∵∠DAQ＝∠OAE，
∴tan∠DAQ＝tan∠OAE，
∴，
∴，
∴m＝﹣9，
∴AQ＝﹣2﹣（﹣9）＝7，DQ＝AQ＝，
∴S梯形COQD＝（DQ+OC）•OQ＝＝，
S△AOC＝，
S△ADQ＝
∴S△ACD＝﹣8﹣＝；
（3）①∵A（﹣2，0），E（0，1），
∴直线DE的解析式为y＝，
设F（t，﹣），P（t，），
∴PF＝﹣＝﹣，
∵PF∥y轴，FG∥x轴，△PFG是等腰直角三角形，
∴点F和G关于抛物线的对称轴x＝对称，∠PFG＝90°，PF＝FG，
∴FG＝2（﹣5﹣t）＝﹣10﹣2t，
∴﹣＝﹣10﹣2t，
∴t1＝，t2＝（舍去），
∴PF＝﹣10﹣2t＝﹣10﹣（﹣7﹣）＝；
②如图2，
当△PEM≌△EPN时，∠EPM＝∠PEM，
∴PM∥EN，即PM∥y轴，
∴xM＝﹣6，
∴yM＝﹣＝4，
∴M（﹣6，4），
如图3，
当△PEM≌△PEN时，∠PEM＝∠PEN，
作PW⊥EM于W，作FG⊥y轴于点F，作AG⊥FG于G，
∴∠G＝∠WFE＝90°，∠AWE＝90°，
∴∠GAW+∠AWG＝90°，∠AWG+∠EWF＝90°，
∴∠GAW＝∠EWF，
∴△EFW∽△WGA，
∴＝，
∵AO⊥EC，
∴AW＝AO＝2，∠AWO＝∠AOE＝90°，
∴∠WAE＝∠OAE，四边形AGFO是矩形，
∴EW＝OE＝1，AG＝OF，FG＝OA＝2，
∴，
设EF＝a，则GW＝2EF＝2a，AG＝OF＝OE+EF＝a+1，
∴WF＝AG＝（a+1），
由WF+GW＝FG得，
，
∴a＝，
∴OF＝，WF＝，
∴W（﹣），
∵E（0，1），
∴直线EW的解析式为：y＝﹣，
由得，
，，
∴M（﹣4，4）或（﹣），
综上所述：M（﹣6，4）或（﹣4，4）或（﹣）．
5．（2024•文昌校级模拟）如图，二次函数y＝ax2﹣4x+c（a≠0）的图象与x轴交于点A、B（3，0），与y轴交于点C（0，3），点P（m，n）是抛物线上的动点．
（1）求抛物线的表达式；
（2）如图1，当m＝2时，求△BCP的面积；
（3）当∠PCB＝15°时，求点P的坐标；
（4）如图2，点Q是抛物线对称轴上一点，是否存在点P，使△POQ是以点P为直角顶点的等腰直角三角形，若存在，请直接写出m的值；若不存在，请说明理由．
【解答】解：（1）把B（3，0），点C（0，3）代入二次函数y＝ax2﹣4x+c中得：
，
解得：，
∴抛物线的表达式为：y＝x2﹣4x+3；
（2）∵点P（m，n）是抛物线上的动点，m＝2，
∴n＝4﹣8+3＝﹣1，
∴P（2，﹣1），
设PC的解析式为：y＝kx+b，PC与x轴交于点H，
把C（0，3）和P（2，﹣1）代入得：，
∴，
∴PC的解析式为：y＝﹣2x+3，
当y＝0时，﹣2x+3＝0，
x＝，
∴BH＝OB﹣OH＝3﹣＝，
∴△BCP的面积＝S△BHC+S△PBH＝××3+××1＝3；
（3）如图1，∵C（0，3），B（3，0），
∴OB＝OC＝3，
∵∠BOC＝90°，
∴∠BCO＝45°，
∵∠PCB＝15°，
∴∠OCH＝45°﹣15°＝30°，
∴OH＝CH，
∵OC＝3，
∴OH＝，
∴H（，0），
同理可求得PC的解析式为：y＝﹣x+3，
∴x2﹣4x+3＝﹣x+3，
解得：x1＝0（舍），x2＝4﹣，
∴P（4﹣，6﹣4）；
当点P位于直线BC上方时，P（4﹣，）．
综上，P（4﹣，6﹣4）或（4﹣，）．
（4）如图2，过点P作DE∥x轴，交y轴于D，交对称轴于点E，
由题意得：P（m，m2﹣4m+3），
∵y＝x2﹣4x+3＝（x﹣2）2﹣1，
∴抛物线对称轴是直线x＝2，
∵△OPQ是等腰直角三角形，
∴∠OPQ＝90°，OP＝PQ，
∴∠EPQ+∠OPD＝90°，
∵∠OPD+∠POD＝90°，
∴∠POD＝∠EPQ，
∵∠ODP＝∠PEQ＝90°，
∴△ODP≌△PEQ（AAS），
∴PE＝OD，
∴2﹣m＝m2﹣4m+3，
∴m2﹣3m+1＝0，
∴m1＝（如图3），m2＝；
如图4，过点P作DE∥x轴，交y轴于D，交对称轴于点E，
同理可得：PE＝OD，
∴2﹣m＝﹣m2+4m﹣3，
∴m2﹣5m+5＝0，
解得：m1＝，m2＝，
综上，m的值是或．
6．（2024•东昌府区模拟）如图，抛物线y＝ax2+bx+c过x轴上点A（﹣1，0）、点B（5，0），过y轴上点C（0，﹣5），点P（m，n）（0＜m＜5）是抛物线上的一个动点．
（1）求该二次函数的表达式；
（2）求四边形OCPB面积的最大值；
（3）当点P的横坐标m满足2＜m＜5时，过点P作PE⊥x轴，交BC于点E，再过点P作PF∥x轴，交抛物线于点F，连接EF，求使△PEF为等腰直角三角形的点P的坐标．
【解答】解：（1）将A（﹣1，0），B（5，0），C（0，﹣5）代入 y＝ax2+bx+c得：
，
解得，
∴二次函数的表达式为y＝x2﹣4x﹣5；
（2）设直线BC的表达式为y＝kx+t，
将B（5，0），C（0，﹣5）代入y＝kx+t得：，
解得，
∴直线BC的表达式为y＝x﹣5，
过点P作PQ⊥x轴，交BC于点E，交x轴于点Q，如图，
∵P（m，n）（0＜m＜5），
∴P（m，m2﹣4m﹣5），E（m，m﹣5），
∴PE＝（m﹣5）﹣（m2﹣4m﹣5）＝﹣m2+5m，
S四边形OCPB＝S△BOC+S△PBC＝S△BOC+S△PEC+S△PEB
＝
＝
＝+（﹣m2+5m）×5
＝﹣m2+m+
＝，
∵，
∴当时，四边形OCPB的面积最大为；
（3）如图，
∵y＝x2﹣4x﹣5＝（x﹣2）2﹣9，
∴抛物线对称轴为直线x＝2，
当点P的横坐标m满足2＜m＜5时，点P在对称轴右侧，
∴PF＝2（m﹣2）＝2m﹣4，
同（2）知PE＝（m﹣5）﹣（m2﹣4m﹣5）＝﹣m2+5m，
当PE＝PF时，△PEF为等腰直角三角形，
∴﹣m2+5m＝2m﹣4，
整理得：m2﹣3m﹣4＝0，
解得：m＝4或 m＝﹣1（不符合题意，舍去），
此时n＝42﹣4×4﹣5＝﹣5，即点P（4，﹣5），
∴当点P的坐标为（4，﹣5）时，△PEF为等腰直角三角形．
7．（2023•阜新模拟）如图，在平面直角坐标系中，直线y＝x+4与x轴，y轴分别交于点A，C，抛物线y＝﹣x2+bx+c过点A和点C，与x轴交于点B．
（1）求这个二次函数的表达式；
（2）抛物线对称轴与直线AC交于点D，若P是直线AC上方抛物线上的一个动点（点P不与点A，C重合），求△PAD面积的最大值；
（3）点M是抛物线对称轴上的一动点，x轴上方的抛物线上是否存在点N，使得△ANM是以AN为直角边的等腰直角三角形；若存在，请直接写出点N坐标；若不存在，请说明理由．
【解答】解：（1）对于直线y＝x+4，令x＝0，则y＝4；令y＝0，则x＝﹣4；∴A（﹣4，0），C（0，4），把A（﹣4，0），C（0，4）代入y＝﹣x2+bx+c得：
，
解得，
∴y＝﹣x2﹣3x+4；
（2）过P作PK∥y轴交AC于K，如图1：
在y＝﹣x2﹣3x+4中，对称轴为直线，
当时，，
∴，
设P（m，﹣m2﹣3m+4），则K（m，m+4），
∴PK＝﹣m2﹣3m+4﹣（m+4）＝﹣m2﹣4m，
∴
＝，
∵，
∴当m＝﹣2时，S△AED取最大值为5；
∴△PAD面积的最大值为5；
（3）x轴上方的抛物线上存在点N，使得△ANM是以AN为直角边的等腰直角三角形，理由如下：
∵A（﹣4，0），对称轴为直线，
设N（t，﹣t2﹣3t+4），
当∠ANM＝90°，AN＝MN，过点N作x轴的平行线交对称轴于点F，过点A作y轴的平行线交NF于点E，如图2，
∴∠ANE＝90°﹣∠FNM＝∠NMF，
∴△ANE≌△NMF（AAS），
∴AE＝NF，EN＝FM，
∴，
整理得，
解得，
∴点N坐标为或；
当∠MAN＝90°，AM＝AN，过点N作x轴的垂线交x轴于点F，对称轴直线交x轴于点E，如图3，
同理△AME≌△NAF，则AE＝NF，即，
整理得，
解得，
∴点N坐标为或；
综上，点N坐标为或或或．