全国通用 中考数学 二次函数压轴题专题练习 14相似三角形存在性问题（不含答案版）

这是一份全国通用 中考数学 二次函数压轴题专题练习 14相似三角形存在性问题（不含答案版），共16页。
判定1：三边对应成比例的两个三角形是相似三角形；
判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；
判定3：有两组角对应相等的三角形是相似三角形．
以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题．
1.（2024春•渠县校级月考）如图，一次函数与x轴、y轴分别交于A、C两点，二次函数y＝ax2+bx+c的图象经过A、C两点，与x轴交于另一点B，其对称轴为直线
（1）求该二次函数表达式；
（2）在y轴的负半轴上是否存在一点M，使以点M、O、B为顶点的三角形与△AOC相似，若存在，求出点M的坐标；若不存在，请说明理由；
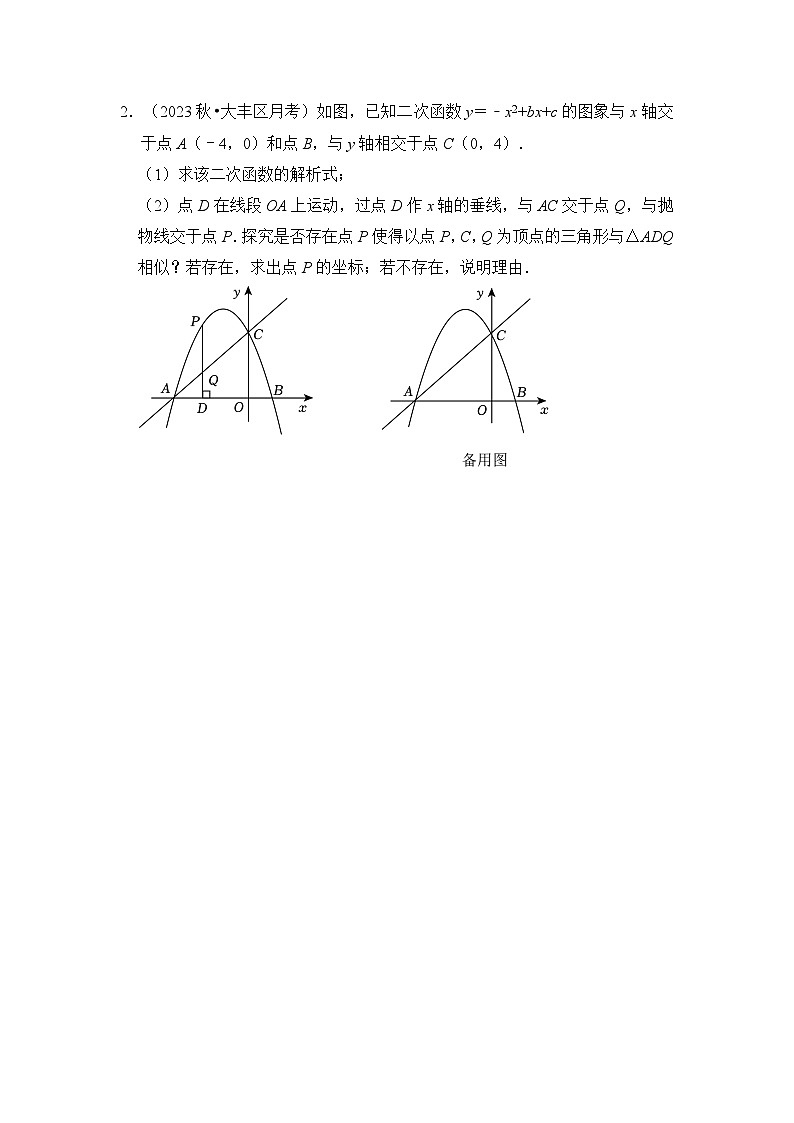
2．（2023秋•大丰区月考）如图，已知二次函数y＝﹣x2+bx+c的图象与x轴交于点A（﹣4，0）和点B，与y轴相交于点C（0，4）．
（1）求该二次函数的解析式；
（2）点D在线段OA上运动，过点D作x轴的垂线，与AC交于点Q，与抛物线交于点P．探究是否存在点P使得以点P，C，Q为顶点的三角形与△ADQ相似？若存在，求出点P的坐标；若不存在，说明理由．
3．（2024秋•仓山区校级月考）如图，二次函数y＝ax2+bx﹣4的图象与x轴交于A，B两点，且经过点C，点A，C的坐标分别为A（﹣1，0），C（2，﹣6）．
（1）求该二次函数的解析式；
（2）点G是线段AC上的动点（点G与线段AC的端点不重合），若△ABG与△ABC相似，求点G的坐标．
4．（2023秋•开福区校级月考）如图，抛物线y＝﹣x2+bx+3交x轴负、正半轴于A，B两点，交y轴于点C，连接AC，tan∠OAC＝3，△ABC的外接圆的圆心为M．
（1）求该二次函数的解析式；
（2）在AC段的抛物线上是否存在一点P，使，若存在请求出点P坐标，若不存在，说明理由；
（3）圆上是否存在Q点，使△AOC与△BQC相似？若存在，直接写出点Q坐标；若不存在，说明理由．
5．（2024•内蒙古）如图，在平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）的图象经过原点和点A（4，0）．经过点A的直线与该二次函数图象交于点B（1，3），与y轴交于点C．
（1）求二次函数的解析式及点C的坐标；
（2）点P是二次函数图象上的一个动点，当点P在直线AB上方时，过点P作PE⊥x轴于点E，与直线AB交于点D，设点P的横坐标为m．
①m为何值时线段PD的长度最大，并求出最大值；
②是否存在点P，使得△BPD与△AOC相似．若存在，请求出点P坐标；若不存在，请说明理由．
6．（2024•南皮县三模）如图，在平面直角坐标系中，直线y＝ax+b1与x轴交于点B（﹣2，0），与y轴交于点C（0，2），二次函数y＝﹣x2+b2x+c的图象过B、C两点，且与x轴交于另一点A，点M为线段OB上的一个动点，过点M作直线l平行于y轴交BC于点F，交二次函数y＝﹣x2+b2x+c的图象于点E．
（1）求一次函数及二次函数的表达式；
（2）求△ABC的面积；
（3）当以点C、E、F为顶点的三角形与△ABC相似时，求线段EF的长度．
7．（2024•阎良区校级二模）如图，二次函数y＝ax2+bx+3的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）求二次函数的表达式；
（2）连接AC，P为第一象限内抛物线上一点，过点P作PD⊥x轴于点D，连接PA，是否存在一点P，使得△PDA与△COA相似，若存在，请求出满足条件的点P的坐标，若不存在，请说明理由．
8．（2024•涟水县模拟）如图，二次函数y＝﹣x2+bx+c的图象与x轴交于A（，0）、B（4，0）两点，与y轴交于点C．
（1）求这个二次函数的表达式；
（2）作直线x＝t（0＜t＜4），分别交x轴、线段BC、抛物线于D、E、F三点，连接CF，若以B、D、E为顶点的三角形与以C、E、F为顶点的三角形相似，求t的值；
（3）点M为y轴负半轴上一点，且OM＝2，将抛物线沿x轴的负方向平移得到新抛物线，点B的对应点为点B'，点C的对应点为点C′，C′B与CB′交于点N．在抛物线平移过程中，当MB′+MC′的值最小时，试求△B′NC′的面积．
9．（2024•工业园区校级二模）已知，关于x的二次函数y＝ax2+2ax﹣3a（a＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，图象顶点为D，连接AC、BC、CD．
（1）请直接写出点A、B、C、D的坐标（用数字或含a的式子表示）：
A ；B ；C ；D ；
（2）作出点C关于对称轴的对称点E，连接AE、CE、DE，若△ACE和△DCE相似，求a的值；
（3）若∠ACB≥90°，直接写出a的取值范围．
10．（2024•岱岳区二模）如图①，已知抛物线y＝ax2﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴交于点E，且OC＝3OE．
（1）求出抛物线的解析式；
（2）如图②Q（t，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，若以点C、O、M、N为顶点的四边形是平行四边形，求出Q点的坐标；
（3）若N点在直线BC的上方，连结CN，①若△MCN与△BQM相似，请求出点Q的坐标；
②将△CMN沿CN翻折，M的对应点为M'，是否存在点Q，使得M'恰好落在y轴正半轴上？若存在，请直接写出Q的坐标．
11．（2024•思明区校级二模）如图，已知二次函数y＝ax2+bx+c的图象与x轴交于A和B（3，0）两点，与y轴交于C（0，﹣2），对称轴为直线，连接BC，在线段BC上有一动点P，过点P作y轴的平行线交二次函数的图象于点N，交x轴于点M，
（1）求抛物线的函数解析式：
（2）请你从以下三个选项中，任选一个为条件，另一个作结论，组成一个真命题，并证明．
①P的横坐标为；②△PCN与△BPM相似；③
（3）若动点P横坐标记为t，△CBN的面积记为S1，△CBM的面积记为S2，且S＝S1﹣S2，写出S与t的函数关系，并判断S是否有最大值，若有请求出；若没有请说明理由．
12．（2024春•赣榆区校级月考）如图，二次函数y＝ax2+bx+c（a＜0）的图象与x轴交于A（﹣1，0），B两点，与y轴交于点C，已知OB＝3OA，OC＝OB．
（1）求该二次函数的表达式；
（2）点M为抛物线对称轴上一动点，是否存在点M使得|BM﹣CM|有最大值，若存在，请直接写出其最大值及此时点M坐标，若不存在，请说明理由．
（3）连接AC，P为第一象限内抛物线上一点，过点P作PD⊥x轴，垂足为D，连接PA，若△PDA与△COA相似，请求出满足条件的P点坐标：若没有满足条件的P点，请说明理由．
13．（2024•邹城市二模）如图，二次函数的图象与x轴交于A（﹣1，0），B（4，0）两点，与y轴交于点C（0，3），点P是直线BC上方抛物线上的一个动点，连接BC，过点P作PQ⊥BC，垂足为Q．
（1）求抛物线的解析式；
（2）求PQ的最大值；
（3）连接CP，抛物线上是否存在点P，使得以C、P、Q为顶点的三角形与△BOC相似？如果存在，请求出点P坐标；如果不存在，请说明理由．
14．（2024•科尔沁区模拟）如图，已知二次函数y＝ax2+bx+3（a≠0）的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C，点P是抛物线上点A与点C之间的动点（不包括点A，点C）．
（1）求此二次函数的解析式；
（2）如图1，连结PA，PC，求△PAC的面积的最大值；
（3）如图2，过点P作x轴的垂线交于点D，与AC交于点Q．探究是否存在点P，使得以点P、C、Q为顶点的三角形与△ADQ相似？若存在，直接写出点P的坐标；若不存在，说明理由．
15．（2024春•游仙区月考）如图，二次函数y＝﹣x2+bx+c（b＞0）的图象与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C（0，4），二次函数的最大值为，P为直线BC上方抛物线上的一动点．
（1）求抛物线和直线BC的解析式；
（2）如图1，过点P作PD⊥BC，垂足为D，连接CP．是否存在点P，使以点C，D，P为顶点的三角形与△AOC相似？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，点Q也是直线BC上方抛物线上的一动点（点Q在点P的左侧），分别过点P，Q作y轴的平行线，分别交直线BC于点M，N，连接PQ．若四边形PQNM是平行四边形，且周长l最大时，求l的最大值及相应的点P的横坐标．
16．（2024•金坛区二模）如图，在平面直角坐标系xOy中，二次函数y＝x2+bx+4的图象与x轴正半轴交于点A、B，与y轴交于点C，OC＝4OA，点P是线段BC上一点（不与点B、C重合），过点P作PQ⊥x轴，交抛物线于点Q，连接OQ，四边形OCPQ是平行四边形．
（1）填空：b＝ ；
（2）求四边形OCPQ的面积；
（3）若点D是OC的中点，连接AD、AC．点E（5，4）是抛物线上一点，F是直线QE上一点，连接BE、BF．若△BEF与△ADC相似，求点F的坐标．