
所属成套资源:全国通用 中考数学 二次函数压轴题专题练习
全国通用 中考数学 二次函数压轴题专题练习 18数学建模(含答案解析版)
展开
这是一份全国通用 中考数学 二次函数压轴题专题练习 18数学建模(含答案解析版),共22页。
【解答】解:任务1:由题意得,A(0,0.72),顶点为(0.3,0.75).
∴可设抛物线的函数表达式为y=a(x﹣0.3)2+0.75.
又抛物线过A(0,0.72),
∴0.72=0.09a+0.75.
∴a=﹣.
∴抛物线的函数表达式为y=﹣(x﹣)2+.
任务2:由题意,∵喷泉池的半径为2.1米,
∴令x=2.1,则y=﹣(2.1﹣)2+=﹣0.33.
∴喷水口升高的最小值为|﹣0.33|=0.33(米).
任务3:当y=﹣(x﹣)2+向上平移个单位,
∴y=﹣(x﹣)2++.
令y=0,即0=﹣(x﹣)2++.
∴当x=2.3或x=﹣1.7(舍去).
∴2.3﹣2.1=0.2(米).
∴建议花卉的种植宽度为0.2米.
对应练习:
1.(2024•青岛)5月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季.为了解樱桃的收益情况,从第1天销售开始,小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析:
A樱桃园:
第x天的单价、销售量与x的关系如表:
第x天的单价与x近似地满足一次函数关系,已知每天的固定成本为745元.
B樱桃园:
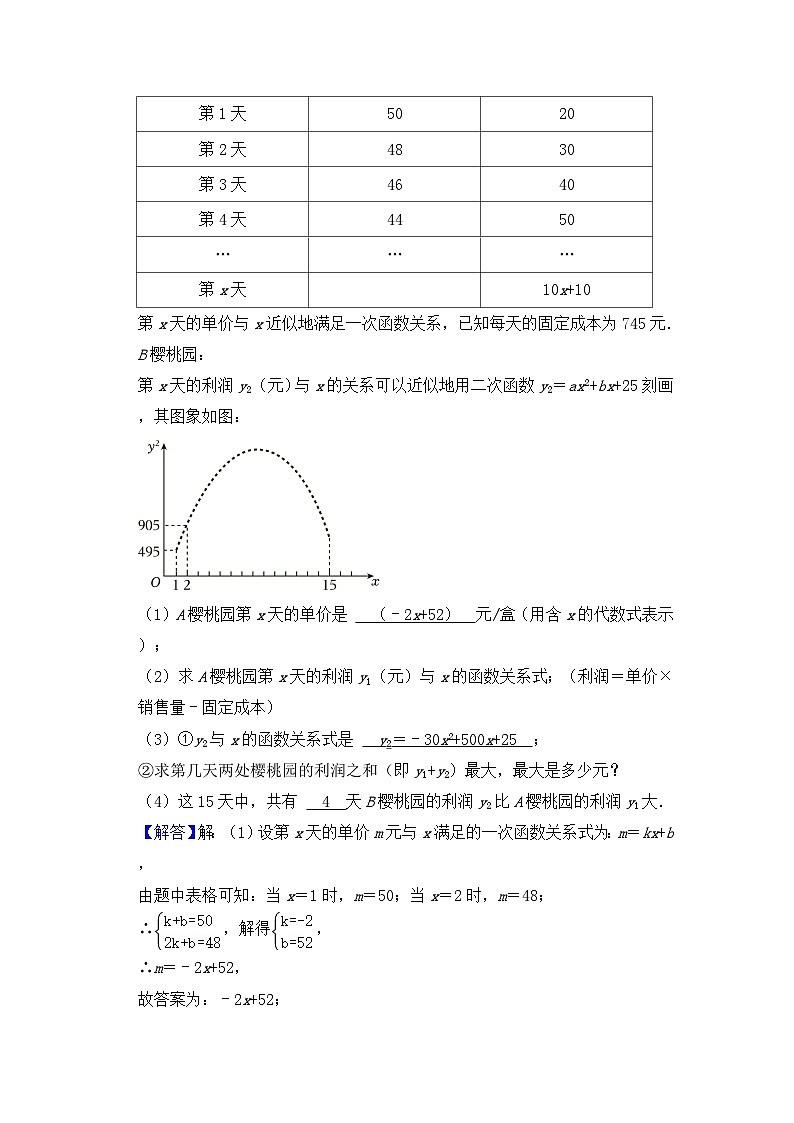
第x天的利润y2(元)与x的关系可以近似地用二次函数y2=ax2+bx+25刻画,其图象如图:
(1)A樱桃园第x天的单价是 (﹣2x+52) 元/盒(用含x的代数式表示);
(2)求A樱桃园第x天的利润y1(元)与x的函数关系式;(利润=单价×销售量﹣固定成本)
(3)①y2与x的函数关系式是 y2=﹣30x2+500x+25 ;
②求第几天两处樱桃园的利润之和(即y1+y2)最大,最大是多少元?
(4)这15天中,共有 4 天B樱桃园的利润y2比A樱桃园的利润y1大.
【解答】解:(1)设第x天的单价m元与x满足的一次函数关系式为:m=kx+b,
由题中表格可知:当x=1时,m=50;当x=2时,m=48;
∴,解得,
∴m=﹣2x+52,
故答案为:﹣2x+52;
(2)根据题意可得:y1=(﹣2x+52)(10x+10)﹣745,
化简整理得:,
∴A樱桃园第x天的利润y1(元)与x的函数关系式为:;
(3)①由图象可知:二次函数的图象经过点(1,495)、(2,905),
∴,解得,
∴y2=﹣30x2+500x+25,
故答案为:y2=﹣30x2+500x+25;
②=﹣50x2+1000x﹣200
=﹣50(x﹣10)2+4800,
∵﹣50<0,
∴当x=10时,y1+y2有最大值4800,
∴第10天两处的樱桃园的利润之和最大,最大是4800元;
(4)由题可知:y2>y1,
∴﹣30x2+500x+25>﹣20x2+500x﹣225即﹣10x2>﹣250,
解得:﹣5<x<5,
∵x取正整数,
∴1≤x≤4,
∴这15天中共有4天B樱桃园的利润y2比A樱桃园的利润y1大,
故答案为:4.
2.(2024•盐城)请根据以下素材,完成探究任务.
【解答】解:任务1:根据题意安排70名工人加工一批夏季服装,
∵安排x名工人加工“雅”服装,y名工人加工“风”服装,
∴加工“正”服装的有(70﹣x﹣y)人,
∵“正”服装总件数和“风”服装相等,
∴(70﹣x﹣y)×1=2y,
整理得:;
任务2:根据题意得:“雅”服装每天获利为:x[100﹣2(x﹣10)],
∴w=2y×24+(70﹣x﹣y)×48+x[100﹣2(x﹣10)],
整理得:w=(﹣16x+1120)+(﹣32x+2240)+(﹣2x2+120x),
∴w=﹣2x2+72x+3360(x>10),
任务3:由任务2得w=﹣2x2+72x+3360=﹣2(x﹣18)2+4008,
∴当x=18时,获得最大利润,
,
∴x≠18,
∵开口向下,
∴取x=17或x=19,
当x=17时,,不符合题意;
当x=19时,,符合题意;
∴70﹣x﹣y=34,
综上:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”服装,即可获得最大利润.
3.(2024•鄞州区校级一模)根据下列素材,探索完成任务.
【解答】解:(1)以最高点为坐标系原点,水平方向为x轴,则设y=ax2,经过 ,
∴,
∴,
∴;
(2)由题意得:y轴上有一人,则左边2人,右边3人,
(或左右互换) 则最右边1人(站在点H处)的横坐标为1.5,
当x=1.5时,,
5,
因此最矮的女生也无法顺利通过头顶.
(3)当跳绳点距离地面1.65米,即y=﹣0.35时,,
解得,
考虑右边第二名队员,当 时,×,
距离地面1.85米,高于最高的队员;
当 时,即最左边队员在 横坐标位置;
当 时,最右边队员在 横坐标位置,则最左边队员在﹣横坐标位置;
∴最左边队员的横坐标为﹣﹣.
4.(2024•山西)综合与实践
问题情境:如图1,矩形MNKL是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB组成的封闭图形,点A,B在矩形的边MN上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校面向全体同学征集设计方案.
方案设计:如图2,AB=6米,AB的垂直平分线与抛物线交于点P,与AB交于点O,点P是抛物线的顶点,且PO=9米.欣欣设计的方案如下:
第一步:在线段OP上确定点C,使∠ACB=90°,用篱笆沿线段AC,BC分隔出△ABC区域,种植串串红;
第二步:在线段CP上取点F(不与C,P重合),过点F作AB的平行线,交抛物线于点D,E.用篱笆沿DE,CF将线段AC,BC与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.
方案实施:学校采用了欣欣的方案,在完成第一步△ABC区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定DE与CF的长.为此,欣欣在图2中以AB所在直线为x轴,OP所在直线为y轴建立平面直角坐标系.请按照她的方法解决问题:
(1)在图2中画出坐标系,并求抛物线的函数表达式;
(2)求6米材料恰好用完时DE与CF的长;
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段AC,BC上.直接写出符合设计要求的矩形周长的最大值.
【考点】二次函数综合题.
【专题】代数几何综合题;二次函数图象及其性质;矩形 菱形 正方形;推理能力.
【解答】解:(1)建立如图所示的平面直角坐标系,
∵OP所在直线是AB的垂直平分线,且AB=6,
∴.
∴点B的坐标为(3,0),
∵OP=9,
∴点P的坐标为(0,9),
∵点P是抛物线的顶点,
∴设抛物线的函数表达式为y=ax2+9,
∵点B(3,0)在抛物线y=ax2+9 上,
∴9a+9=0,
解得:a=﹣1.
∴抛物线的函数表达式为y=﹣x2+9(﹣3≤x≤3);
(2)点D,E在抛物线y=﹣x2+9 上,
∴设点E的坐标为(m,﹣m2+9),
∵DE∥AB,交y轴于点F,
∴DF=EF=m,OF=﹣m2+9,
∴DE=2m.
∵在Rt△ABC中,∠ACB=90°,OA=OB,
∴.
∴CF=OF﹣OC=﹣m2+9﹣3=﹣m2+6,
根据题息,得DE+CF=6,
∴﹣m2+6+2m=6,
解得:m1=2,m=0(不符合题意,舍去),
∴m=2.
∴DE=2m=4,CF=﹣m2+6=2
答:DE的长为4米,CF的长为2米;
(3)如图矩形灯带为GHML,
由点A、B、C的坐标得,直线AC和BC的表达式分别为:y=x+3,y=﹣x+3,
设点G(m,﹣m2+9)、H(﹣m,﹣m2+9)、L(m,m+3)、M(﹣m,m+3),
则矩形周长=2(GH+GL)=2(﹣2m﹣m2+9﹣m﹣3)=﹣2(m+1.5)2+≤,
故矩形周长的最大值为米.
5.(2024•深圳)在综合实践课上,数学探究小组用两个互相垂直的直尺制作了一个“T”形尺,并用它对二次函数图象的相关性质进行研究.
把“T”形尺按图1摆放,水平宽AB的中点为C,图象的顶点为D,测得AB为m厘米时,CD为n厘米.
【猜想】
(1)探究小组先对y=x2的图象进行多次测量,测得m与n的部分数据如表:
描点:以表中各组对应值为点的坐标,在图2的直角坐标系内描出相应的点.
连线:用光滑的曲线顺次连接各点.
猜想:n与m的关系式是 n=m2
【验证】
(2)探究小组又对多个二次函数的图象进行了测量研究,发现测得的n与m也存在类似的关系式,并针对二次函数y=a(x﹣h)2+k(a>0)的情况进行了推理验证.请从下表中任选一种方法(在“□”内打“√”)并补全其推理过程;(根据需要,选用字母a,m,n,h,k表示答案)
【应用】
(3)已知AB∥x轴且AB=4,两个二次函数y=2(x﹣h)2+k和y=a(x﹣h)2+d的图象都经过A,B两点.当两个函数图象的顶点之间的距离为10时,求a的值.
【解答】解:(1)描点连线绘制函数图象如下:
由题意得,点B(m,n),
将点B的坐标代入函数表达式得:n=(m)2=m2;
故答案为:n=m2;
(2)方案一:
点B′(m,n),
将点B′的坐标代入抛物线表达式得:n=a×m2,
故答案为:(m,n),n=am2;
方案二:
点B(h+m,k+n)
将点B的坐标代入抛物线表达式得:k+n=a(h+m﹣h)2+k,
解得:n=am2,
故答案为:(h+m,k+n),n=am2;
(3)①当a>0时,此时抛物线开口方向向上,
由(2)知a=,h=,
∵y=2(x﹣h)2+k,
∴h1==8,
∵两个函数图象的顶点之间的距离为10,
∴h2=18,
∴a===;
②当a<0时,同理可得:h2=﹣2,此时a=﹣
综上,a=或﹣.
6.(2024•福田区二模)根据以下素材,探索完成任务.
【解答】解:任务1:
设抛物线解析式为:y=ax2+bx,
抛物线过顶点(2,3),M(4,0),
∴,
∴,
∴抛物线解析式为:y=﹣x2+3x.
任务2:
∵形状相同,最高高度也相同,
∴设顶点坐标为(m,3),其中m>0,
∴设抛物线解析式为:y=(x﹣m)2+3,
∵抛物线过A(0,),
∴=(﹣m)2+3,
∴m2=1,
∴m=±1,
∵m>0,
∴m=1,
∴抛物线解析式为:y=(x﹣1)2+3,
当y=0时,
(x﹣1)2+3=0,
∴x1=3,x2=﹣1,
∴OB=3,
即喷泉跨度OB的最小值为3.
任务3:
设F(n,h),则E(n+2,h),
∴,
∴,
∴能够进入该安全通道的人的最大身高为≈1.3(m).
7.根据以下素材,探索完成任务.
如何探测弹射飞机的轨道设计
素材1:图1是某科技兴趣小组的同学们制做出的一款弹射飞机,为验证飞机的一些性能,通过测试收集发现飞机相对于出发点的飞行水平距离x(单位:m)随飞行时间t(单位:s)的变化满足一次函数关系;飞行高度y(单位:m)随飞行时间t(单位:s)的变化满足二次函数关系.数据如下表所示.
素材2:图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台PQ,当弹射口高度变化时,飞机飞行的轨迹可视为抛物线上下平移得到,线段AB为飞机回收区域,已知AP=88m.AB=8m.
问题解决:
任务1:确定函数表达式.
①直接写出x关于t的函数表达式: x=4t .
②求出y关于t的函数表达式.
任务2:探究飞行距离.当飞机落地(高度为0m)时,求飞行的水平距离.
任务3:确定弹射口高度h.当飞机落到回收区域AB内(不包括端点A,B)时,请写出发射台PQ弹射口高度h的变化范围: 22<h<48 .
【解答】解:(1)①设x=kt+b,将(0,0),(2,8)代入得:
,
解得:,
∴x关于t的函数表达式为x=4t,
故答案为:x=4t;
②设y关于t的函数表达式为y=at2+bt+c(a≠0),将(0,0),(2,18),(4,32)代入得:
,
解得:,
故y关于t的函数表达式为y=﹣t2+10t;
(2)当飞机落地时,即y=0,
∴﹣t2+10t=0,
解得,t=20或t=0(不合题意,舍去),
∵x=4t,
∴t=20时,x=4×20=80,
故飞机落地时,飞行的水平距离为80m;
(3)任务3:由x=4t和y=﹣t2+10t得:y=﹣x2+x,
设发射台弹射口高度为h,则此时抛物线的表达式为:y=﹣x2+x+h,
当x=AP=88时,﹣×882+×88+h=0,
解得:h=22,
当x=BP=88+8=96时,﹣×962+×96+h=0,
解得:h=48,
即22<h<48,
故答案为:22<h<48.
8.【项目式学习】
项目主题:设计落地窗的遮阳篷.
项目背景:小明家的窗户朝南,窗户的高度AB=2m,为了遮挡太阳光,小明做了以下遮阳蓬的设计方案,请根据不同设计方案完成以下任务.
方案1:直角形遮阳篷
如图1,小明设计的第一个方案为直角形遮阳篷BCD,点C在AB的延长线上CD⊥AC.
(1)若BC=0.5m,CD=1m,则支撑杆BD= m.
(2)小明发现上述方案不能很好发挥遮阳作用,如图2,他观察到此地一年中的正午时刻,太阳光与地平面的最小夹角为α,最大夹角为β.小明查阅资料,计算出,,为了让遮阳篷既能最大限度地使冬天温暖的阳光射入室内(太阳光与BD平行),又能最大限度地遮挡夏天炎热的阳光(太阳光与AD平行).请求出图2中BC,CD的长度.
方案2:抛物线形遮阳篷
(3)如图3,为了美观及实用性,小明在(2)的基础上将CD边改为抛物线形可伸缩的遮阳篷(F为抛物线的顶点,DF段可伸缩),且∠CFD=90°,BC,CD的长保持不变.若以C为原点,CD方向为x轴,BC方向为y轴.
①求该二次函数的表达式.
②若某时刻太阳光与水平地面夹角θ的正切值,使阳光最大限度地摄入室内,求遮阳蓬点D上升的高度最小值(即点D′到CD的距离).
【解答】解:(1)在Rt△CBD中,∠C=90°,BC=0.5m,CD=1m,
BD===(m),
故答案为:;
(2)由题意得:CD∥AM,BD∥AF,∠C=∠CAM=90°,
∵CD∥AM,
∴∠CDA=∠DAM=β,
∵BD∥AF,
∴∠BDA=∠FAD,
∴∠CDA﹣∠BDA=∠DAM﹣∠FAD,
∴∠CDB=∠FAM=α,
在Rt△CBD中,∠C=90°,
∴tan∠CDB=tanα==,
∴设BC=x m,CD=3x m,
在Rt△ACD中,∠C=90°,tan∠CDA=tanβ==,
∴=,
解得x=,
∴BC=,
CD=2m;
(3)①由F为抛物线顶点,可知FC=FD,
∵∠CFD=90°,
∴△FCD为等腰直角三角形,
由二次函数对称性可知,F(1,1),
设二次函数为:y=ax(x﹣2),代入F(1,1)得:
1=a(﹣1),
解得 a=﹣1,
∴y关于x的关系式为:y=﹣x(x﹣2)=﹣x2+2x;
②BD光线与水平方向的夹角为θ,过D′作x轴的垂线交x轴于点E,过B作y轴的垂线,两条垂线交于点H.即,
设D′H=2a m,BH=3a m,则点,
代入y=﹣x(x﹣2)得:2a﹣=﹣3a(3a﹣2),
化简得27a2﹣12a﹣2=0,
解得,a1=,a2= (不合题意,舍去),
∴D'E=2×﹣=﹣(m),
∴遮阳篷点D上升的高度最小值为m.
素材1
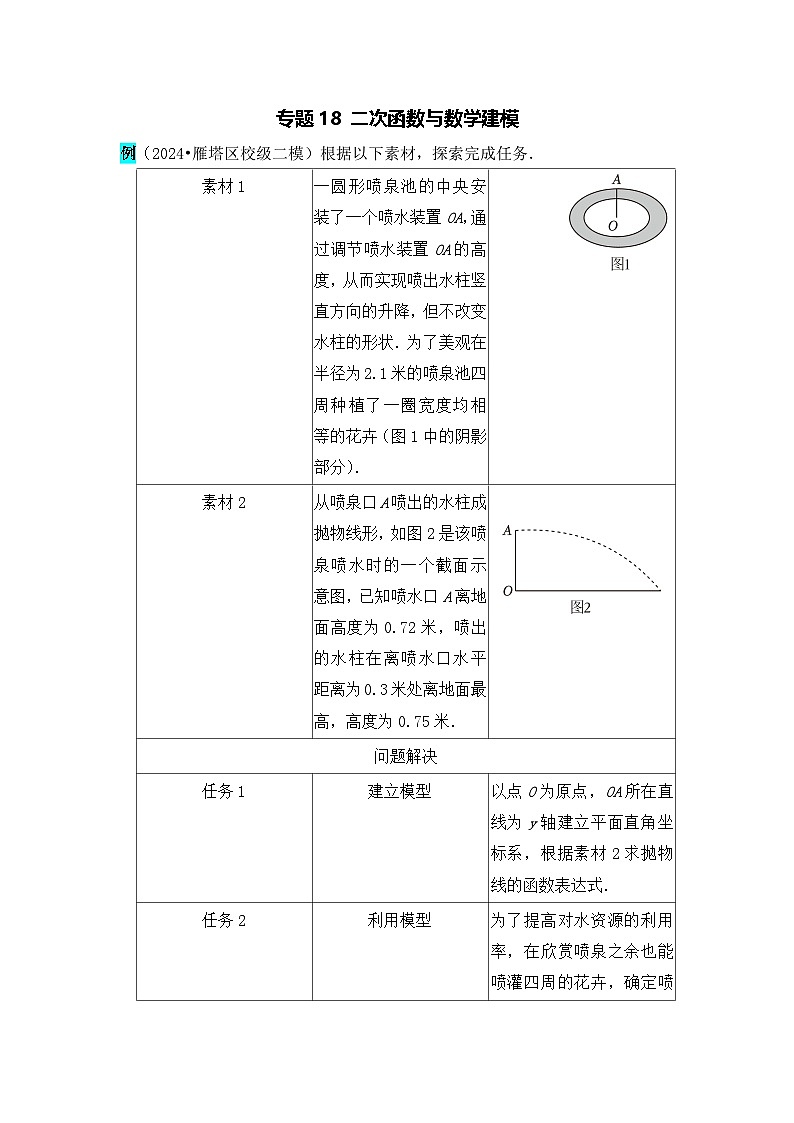
一圆形喷泉池的中央安装了一个喷水装置OA,通过调节喷水装置OA的高度,从而实现喷出水柱竖直方向的升降,但不改变水柱的形状.为了美观在半径为2.1米的喷泉池四周种植了一圈宽度均相等的花卉(图1中的阴影部分).
素材2
从喷泉口A喷出的水柱成抛物线形,如图2是该喷泉喷水时的一个截面示意图,已知喷水口A离地面高度为0.72米,喷出的水柱在离喷水口水平距离为0.3米处离地面最高,高度为0.75米.
问题解决
任务1
建立模型
以点O为原点,OA所在直线为y轴建立平面直角坐标系,根据素材2求抛物线的函数表达式.
任务2
利用模型
为了提高对水资源的利用率,在欣赏喷泉之余也能喷灌四周的花卉,确定喷水口A升高的最小值.
任务3
分析计算
喷泉口A升高的最大值为米,为能充分喷灌四周花卉,请对花卉的种植宽度提出合理的建议.
单价(元/盒)
销售量(盒)
第1天
50
20
第2天
48
30
第3天
46
40
第4天
44
50
…
…
…
第x天
10x+10
制定加工方案
生产背景
背景1
◆某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式.
◆因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或“雅”服装1件,或“正”服装1件.
◆要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
背景2
每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为:
①“风”服装:24元/件;
②“正”服装:48元/件;
③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整理
现安排x名工人加工“雅”服装,y名工人加工“风”服装,列表如下:
服装种类
加工人数(人)
每人每天加工量(件)
平均每件获利(元)
风
y
2
24
雅
x
1
正
1
48
探究任务
任务1
探寻变量关系
求x、y之间的数量关系.
任务2
建立数学模型
设该工厂每天的总利润为w元,求w关于x的函数表达式.
任务3
拟定加工方案
制定使每天总利润最大的加工方案.
如何设计跳绳的方案
素材1
参加跳长绳比赛时,各队跳绳6人,摇绳2人,共计8人,他们在同一平面内站成一路纵队.图2是长绳甩到最高处时的示意图,可以近似的看作一条抛物线.摇绳的两名队员水平间距AB为5米,他们的手到地面的高度AC=BD=1米,绳子最高点距离地面2米.
素材2
某队的6名跳绳队员中,男女生各3名,男生身高均在1.70﹣1.80米,女生身高一人为1.7米高,两人都为1.65米,为保证安全,跳绳队员之间的距离至少0.5米.
问题解决
任务1
确定长绳在最高点时的形状
在图2中建立适当的平面直角坐标系,求抛物线的函数表达式.
任务2
探究站队的方式
若将最高的男生站在摇绳队员的中点,长绳能否顺利甩过所有队员的头顶?
任务3
设计位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式站队,请在你所建立的坐标系中,求出左边第一位队员横坐标的取值范围.
m
0
2
3
4
5
6
…
n
0
1
2.25
4
6.25
9
…
□方法1
□方法2
如图3,平移二次函数图象,使得顶点D移到原点O的位置,则:
A'B'=AB=m,C'O=CD=n,
C'B=,
所以点B′坐标为 (m,n) ;
将点B′坐标代入y=ax2,
得到n与m的关系式是 n=am2 .
如图4,顶点D的横坐标加个单位,纵坐标加n个单位得到点B的坐标,所以点B坐标为 (h+m,k+n) ;
将点B坐标代入y=a(x﹣h)2+k,
得到n与m的关系式是 n=am2 .
如何设计喷泉安全通道?
在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计).
素材1
图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最高高度也相同,水落地点都在喷水管的右侧.
素材2
图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为OM=4m,水柱最高点离地面3m.图3是某一时刻时,水柱形状的示意图.OA为喷水管,B为水的落地点,记OB长度为喷泉跨度.
素材3
安全通道CD在线段OB上,若无论喷头高度如何变化,水柱都不会进入CD上方的矩形区域,则称这个矩形区域CDEF为安全区域.
问题解决
任务1
确定喷泉形状
在图2中,以O为原点,OM所在直线为x轴,建立平面直角坐标系,求出抛物线的函数表达式.
任务2
确定喷泉跨度的最小值
若喷水管OA最高可伸长到2.25m,求出喷泉跨度OB的最小值.
任务3
设计通道位置及儿童的身高上限
现在需要一条宽为2m的安全通道CD,为了确保进入安全通道CD上的任何人都能在安全区域内,则能够进入该安全通道的人的最大身高为多少?(精确到0.1m)
飞行时间t/s
0
2
4
6
8
…
飞行的水平距离x/m
0
8
16
24
32
…
飞行高度y/m
0
18
32
42
48
…
相关试卷
这是一份全国通用 中考数学 二次函数压轴题专题练习 19新定义(含答案解析版),共105页。试卷主要包含了2+2就是“友好二次函数”,定义,我们约定,关于原点O互为“伴随函数”等内容,欢迎下载使用。
这是一份全国通用 中考数学 二次函数压轴题专题练习 18数学建模(不含答案版),共12页。试卷主要包含了请根据以下素材,完成探究任务,根据下列素材,探索完成任务,根据以下素材,探索完成任务,【项目式学习】等内容,欢迎下载使用。
这是一份全国通用 中考数学 二次函数压轴题专题练习 17二次函数与圆(含答案解析版),共24页。试卷主要包含了两点,与y轴交于点C,已知,定义,,直线l是对称轴等内容,欢迎下载使用。








