



湖南省长沙市雅礼教育集团2022-2023学年九年级下学期期中考试数学试题+答案
展开
这是一份湖南省长沙市雅礼教育集团2022-2023学年九年级下学期期中考试数学试题+答案,文件包含雅礼教育集团2022-2023学年九年级下学期期中考试数学试题word原卷docx、雅礼教育集团2022-2023学年九年级下学期期中考试数学试题答案pdf等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
考生注意:本试卷共25道小题,满分120分,时量120分钟
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项。本大题共10个小题,每小题3分,共30分)
1.的倒数是( )
A.B.C.D.
2.今年的长沙热爆了,继连续三周周六超300万人次破记录后,长沙地铁,又一次出圈。连续三天的客流强度,不是第二,就是第一。2023年3月10号,客运量302.1万人次,客流强度1.58全国第二,仅在广州之后,那么302.1万人次这个数据用科学记数法表示为( )
A.人次B.人次
C.人次D.人次
3.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=6,则线段PB的长度为( )
A.3B.4C.6D.7
第3题图 第5题图 第6题图
4.下列运算正确的是( )
A.B.
C.D.
5.如图是六个棱长为1的立方块组成的一个几何体,其俯视图的面积是( )
A.6B.5C.4D.3
6.如图,点B是△ADC的边AD的延长线上一点,DE∥AC.若∠C=50°,∠BDE=55°,则∠CDB的度数等于( )
A.70°B.100°C.105°D.110°
7.某中学体育节,有17名同学参加女子百米赛跑,她们预赛的成绩各不相同,取前8名参加决赛.小雅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这17名同学成绩的( )
A.中位数B.极差C.平均数D.方差
8.如果点P(m,)在第四象限,那么m的取值范围是( )
A.B.C.D.
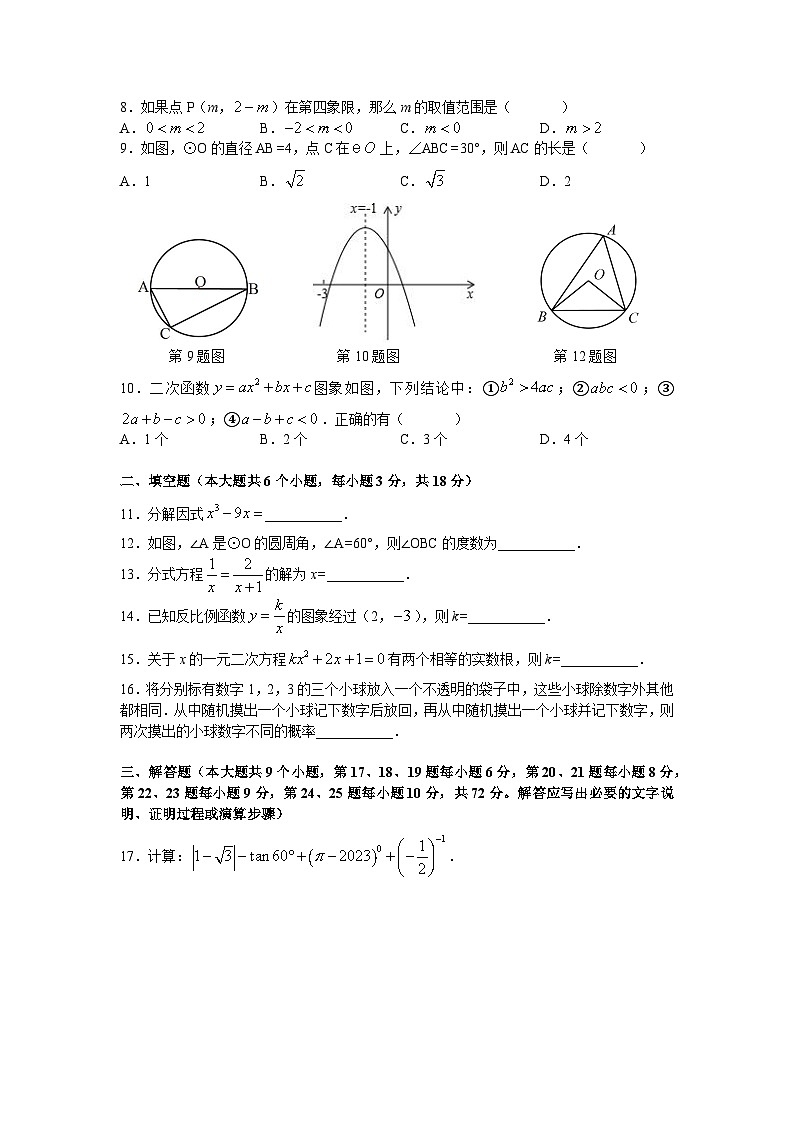
9.如图,⊙O的直径AB=4,点C在上,∠ABC=30°,则AC的长是( )
A.1B.C.D.2
第9题图 第10题图 第12题图
10.二次函数图象如图,下列结论中:①;②;③;④.正确的有( )
A.1个B.2个C.3个D.4个
二、填空题(本大题共6个小题,每小题3分,共18分)
11.分解因式___________.
12.如图,∠A是⊙O的圆周角,∠A=60°,则∠OBC的度数为___________.
13.分式方程的解为x=___________.
14.已知反比例函数的图象经过(2,),则k=___________.
15.关于x的一元二次方程有两个相等的实数根,则k=___________.
16.将分别标有数字1,2,3的三个小球放入一个不透明的袋子中,这些小球除数字外其他都相同.从中随机摸出一个小球记下数字后放回,再从中随机摸出一个小球并记下数字,则两次摸出的小球数字不同的概率___________.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分。解答应写出必要的文字说明、证明过程或演算步骤)
17.计算:.
18.先化简,再求值:,其中.
19.已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.
求证:∠ACE=∠DBF.
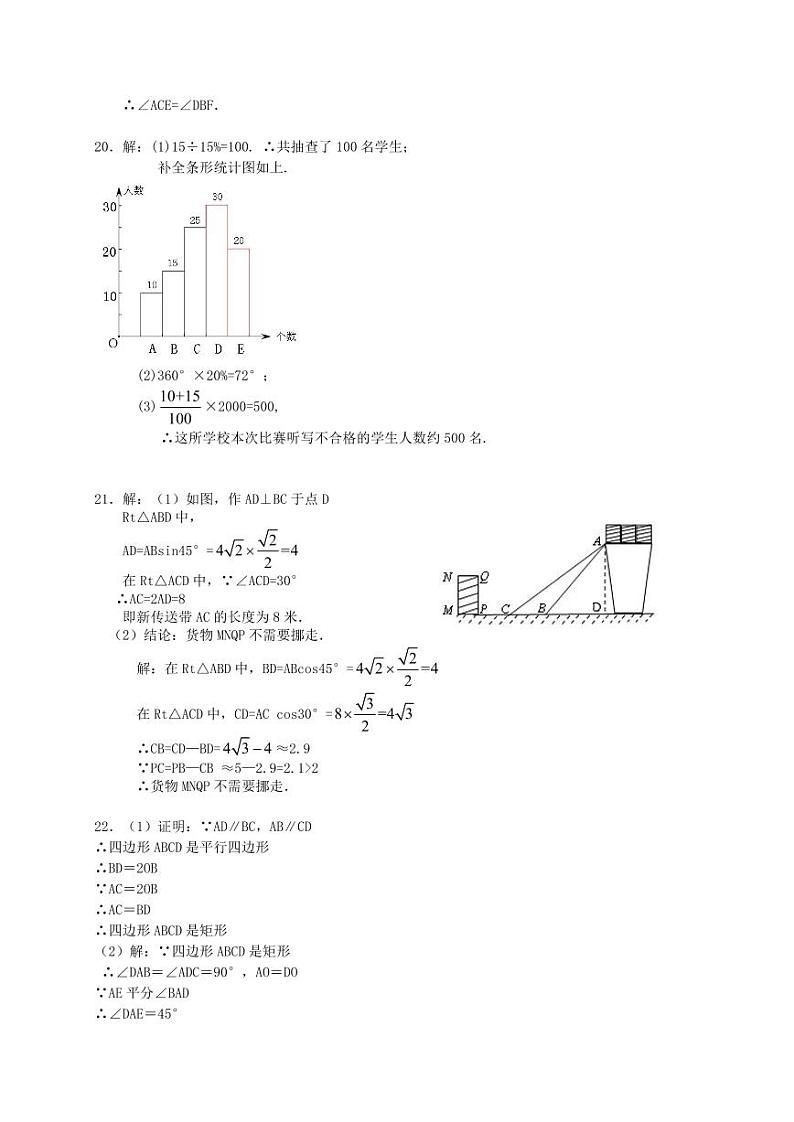
20.某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
(1)本次共随机抽查了___________名学生,并补全条形统计图;
(2)扇形统计图中,组别为E的扇形的圆心角是多少度?
(3)该校共有2000名学生,如果听写正确的个数少于16个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
21.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.(参考数据:,)
22.如图,四边形ABCD的对角线AC,BD相交于点O,其中AD∥BC,AB∥CD,AC=2OB,E为CD上一点,连接AE,OE.
(1)求证:四边形ABCD是矩形;
(2)若AE平分∠BAD,且BD=2AD,求∠DOE的度数.
23.春节是中国的传统节日,每年元旦节后是购物的高峰期,2023年元月某水果商从农户手中购进A、B两种红富士苹果,其中A种红富士苹果进货价为28元/件,销售价为42元/件,其中B种红富士苹果进货价为22元/件,销售价为34元/件。(注:利润=销售价−进货价)
(1)水果店第一次用720元购进A、B两种红富士苹果共30件,求两种红富士苹果分别购进的件数;
(2)第一次购进的红富士苹果售完后,该水果店计划再次购进A、B两种红富士苹果共80件(进货价和销售价都不变),且进货总费用不高于2000元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
(3)春节临近结束时,水果店发现B种红富士苹果还有大量剩余,决定对B种红富士苹果调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,为了尽快减少库存,将销售价定为每件多少元时,才能使B种红富士苹果平均每天销售利润为90元?
24.如图,抛物线与x轴交于A,B两点,与y轴交于C点,已知B点的坐标为(3,0),C点的坐标为(0,3).
(1)求抛物线的解析式;
(2)图1中,点P为抛物线上的动点,且位于第二象限,过P,B两点作直线l交y轴于点D,交直线AC于点E.是否存在这样的直线l:以C,D,E为顶点的三角形与△BOD相似?若存在,请求出这样的直线l的解析式;若不存在,请说明理由.
(3)图2中,点C和点C'关于抛物线的对称轴对称,点M在抛物线上,且∠MCB=∠CBC',求M点的横坐标.
25.圆内各几何要素之间存在一定的数量关系和位置关系,这也是国内外数学家感兴趣的研究对象,其中就有对角线互相垂直的圆内接四边形。我们把这类对角线互相垂直的圆内接四边形称为“雅系四边形”.
(1)若平行四边形ABCD是“雅系四边形”,则四边形ABCD是_________(填序号);
①矩形②菱形③正方形
(2)如图,四边形ABCD内接于圆,P为圆内一点,∠APD=∠BPC=90°,且∠ADP=∠PBC,求证:四边形ABCD为“雅系四边形”;
(3)在(2)的条件下,BD=3,且AB=DC.
①当DC=时,求AC的长度;
②当DC的长度最小时,请直接写出tan∠ADP的值.
相关试卷
这是一份2024年湖南省长沙市雅礼集团中考数学预测卷(含答案),共30页。
这是一份2024年湖南省长沙市雅礼集团中考数学预测卷(一)(含答案),共23页。
这是一份湖南省长沙市雅礼集团2022-2023学年九年级上学期期末考试数学试题,共5页。









