
四川省阆中中学校2023年4月九年级下学期月考数学试卷
展开
这是一份四川省阆中中学校2023年4月九年级下学期月考数学试卷,共15页。试卷主要包含了选择题,填空题,本大题共9小题,共86分.等内容,欢迎下载使用。
(试卷满分:150分 考试时间:120分钟)
一、选择题:本大题共10个小题,每小题4分,共40分.
1. 如果式子的值与-互为倒数,则的值为( )
A.B.-C.-D.
2.中国科学技术大学完成的“祖冲之二号”和“九章二号”量子计算优越性实验入选
2021年国际物理学十大进展.人们发现全球目前最快的超级计算机用时2.3秒的计算量,“祖冲之二号”大约用时仅为0.00000023秒,将数字0.00000023用科学记数法表示为( )
A.B.C.D.
3.计算2x·(-3xy)2·(-x2y)3的结果是( )
A.18x8y5B.6x9y5C.-18x9y5D.-6x4y5
4. 若函数与的图象如图所示,则函数的大致图象为( )
A.B.C.D.
5.2022年北京冬季奥运会中国体育代表团共收获9金、4银、2铜位列奖牌榜第三,金牌数和奖牌数均创历史新高.据统计,近五届冬奥会上中国体育代表团的奖牌数分别是11,11,9,9,15,对于近五届冬奥会获得奖牌数据,下列说法正确的是( )
A.中位数是9B.平均数是10C.众数是11D.方差是4.8
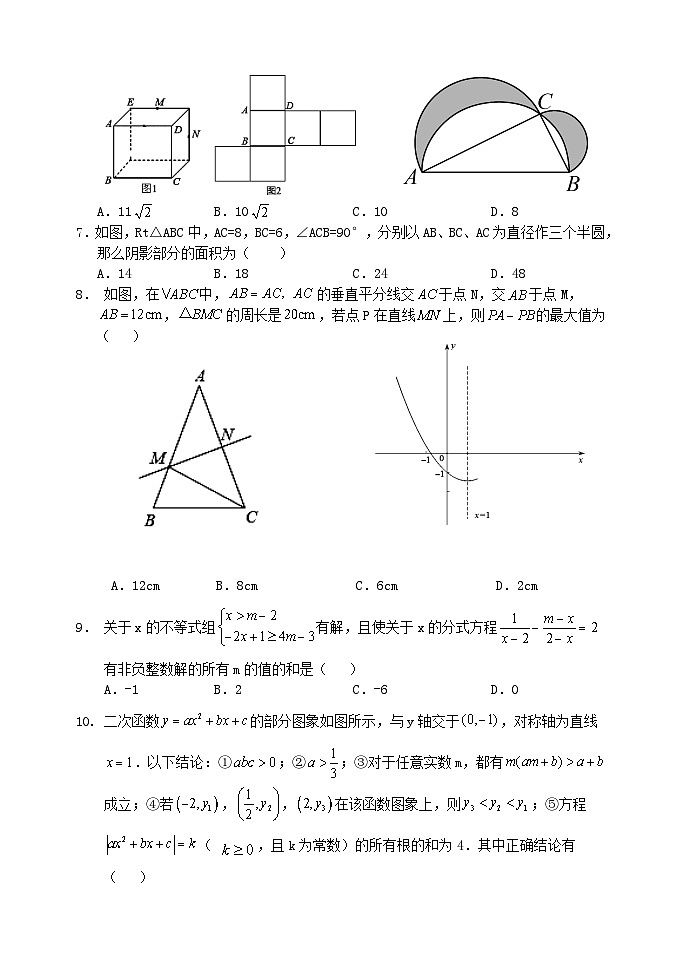
6.图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
A.11B.10C.10D.8
7.如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
A.14B.18C.24D.48
8. 如图,在中,的垂直平分线交于点N,交于点M,,的周长是,若点P在直线上,则的最大值为( )
A.12cmB.8cmC.6cmD.2cm
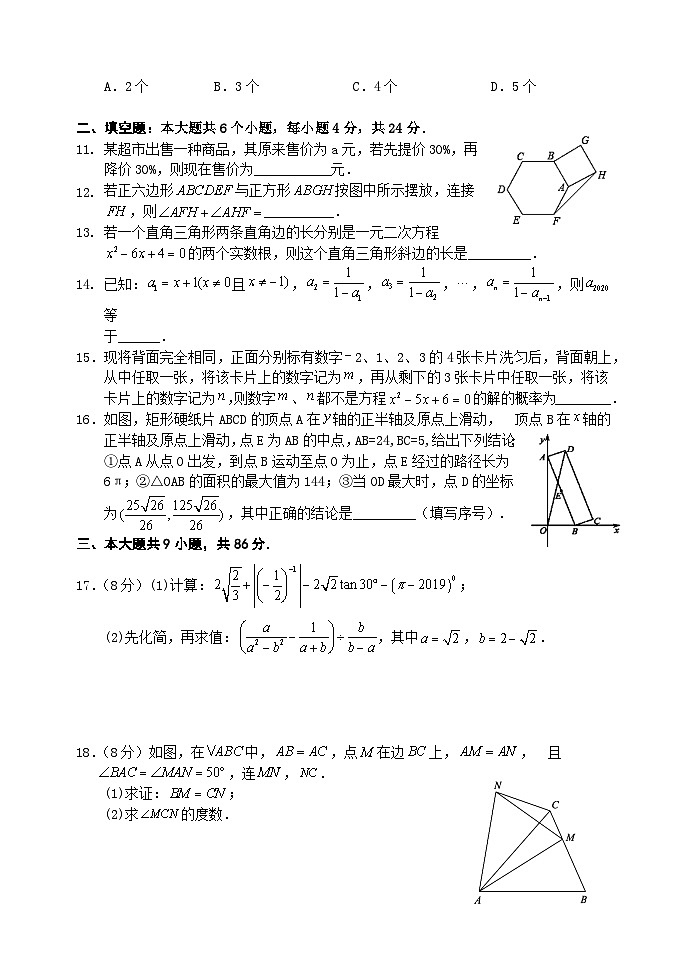
9. 关于x的不等式组有解,且使关于x的分式方程
有非负整数解的所有m的值的和是( )
A.-1B.2C.-6D.0
10. 二次函数的部分图象如图所示,与y轴交于,对称轴为直线.以下结论:①;②;③对于任意实数m,都有成立;④若,,在该函数图象上,则;⑤方程( ,且k为常数)的所有根的和为4.其中正确结论有( )
A.2个B.3个C.4个D.5个
二、填空题:本大题共6个小题,每小题4分,共24分.
11. 某超市出售一种商品,其原来售价为a元,若先提价30%,再
降价30%,则现在售价为___________元.
若正六边形与正方形按图中所示摆放,连接
,则__________.
13. 若一个直角三角形两条直角边的长分别是一元二次方程
的两个实数根,则这个直角三角形斜边的长是_________.
14. 已知:且,,,,,则等
于______.
15.现将背面完全相同,正面分别标有数字2、1、2、3的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数字记为,再从剩下的3张卡片中任取一张,将该卡片上的数字记为,则数字、都不是方程的解的概率为________.
16.如图,矩形硬纸片ABCD的顶点A在轴的正半轴及原点上滑动, 顶点B在轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为6π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为,其中正确的结论是_________(填写序号).
三、本大题共9小题,共86分.
17.(8分)(1)计算:;
(2)先化简,再求值:,其中,.
18.(8分)如图,在中,,点在边上,, 且,连,.
(1)求证:;
(2)求的度数.
19.(8分)为落实“双减提质”,进一步深化“数学提升工程”,提升学生数学核心素养,某学校拟开展“双减”背景下的初中数学活动作业成果展示现场会,为了解学生最喜爱的项目,现随机抽取若干名学生进行调查,并将调查结果绘制成如下两幅不完整的统计图:
根据以上信息,解答下列问题:
(1)参与此次抽样调查的学生人数是____人,并补全统计图①(要求在条形图上方注明人数);
(2)图②中扇形的圆心角度数为_____度;
(3)若参加成果展示活动的学生共有1200人,估计其中最喜爱“测量”项目的学
生人数是多少;
(4)计划在,,,,五项活动中随机选取两项作为直播项目,请用列表
或画树状图的方法,求恰好选中,这两项活动的概率.
20.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象相交于A、B两点,过点A作AD⊥x轴于点D,AO=5,OD=AD,B点的坐标为(﹣6,n).
(1)求一次函数和反比例函数的表达式;
(2)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
21.(10分)为了美化环境,建设宜居成都,我市准备在一个广场 上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用(元)与种植面积之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当和时,与的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共,若甲种花卉的种植面积不少于,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
22.(10分)已知方程的两根是、.
(1)求的值;
(2)求的值;
(3)求作一个新的一元二次方程,使其两根分别等于、的倒数的立方.
(参考公式:.
23.(10分)如图,在中,,平分交 于点,为上一点,经过点,的分别交,于点,,连接交于点.
(1)求证:是的切线;
(2)设,,试用含的代数式表示线段的长;
(3)若,,求的长.
24.(10分)如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
25.(12分)在平面直角坐标系中,已知抛物线与轴交于,两点,与轴交于点.
(1)求抛物线的函数表达式;
(2)如图1,点为第四象限抛物线上一点,连接,交于点,连接,
记的面积为,的面积为,求的最大值;
(3)如图2,连接,,过点作直线,点,分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点,,使.若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.
四川省阆中中学校2023年春初2020级4月月考
数学试题参考答案
一、选择题:本题共10小题,每小题4分,共40分。
二、填空题(24分,每小题4分)
11.; 12.; 13.; 14.; 15. ; 16.①②③
17.【详解】(1)原式 ……………………………………2分
; …………………………………4分
(2)原式
, ……………………………………3分
当,时,原式 ……………………………………4分
18.【详解】(1)证明:∵,
∴,即, ………………………1分
在和中,
∴, ……………………………………3分
∴; ……………………………………4分
(2)解:∵,
∴, ……………………………………6分
∴.…………………8分
19【详解】(1)因为参与活动的人数为36人,占总人数,
所以总人数人, …………………………………1分
则参与活动的人数为:人;
补全统计图如下: …………………………2分
(2)扇形的圆心角为:,故答案为:90; ……………………3分
(3)最喜爱“测量”项目的学生人数是:人; ………………………4分
(4)列表如下:
或者树状图如下: ………………………………6分
所以,选中、这两项活动的概率为:. ……………8分
20.【详解】(1)∵AD⊥x轴,∴∠ADO=90°.
在Rt△AOD中,AO=5,ODAD,∴AD=4,OD=3,∴A(3,4),
∴k=3×4=12,∴y. …………………………………2分
又点B在反比例函数上,∴n2,∴B(﹣6,﹣2).
∵点A(3,4),B(﹣6,﹣2)在直线AB上,∴,∴ ………4分
∴AB直线的表达式为yx+2; ……………………………………5分
(2)设点P(0,m).
∵A(3,4),O(0,0),∴OA=5,OP=|m|,AP. …………………6分
∵△AOP是等腰三角形,∴分三种情况讨论:
①当OA=OP时,∴|m|=5,∴m=±5,∴P(0,5)或(0,﹣5); ………………7分
②当OA=AP时,∴5,∴m=0(舍)或m=8,∴P(0,8);………8分
③OP=AP时,∴|m|,∴m,∴P(0,). …………………9分
综上所述:当P点坐标为(0,8),(0,5),(0,﹣5)或(0,)时,△AOP是等腰三角形. ……………………………………10分
21.【详解】(1) ……………………………………4分
(2)设甲种花卉种植面积为,则乙种花卉种植面积为.
. ……………………………………5分
当时,. …………………………6分
当时,元. ………………………………………7分
当时,. ………………………………8分
当时,元. ………………………………………9分
,当时,总费用最低,最低为119000元.
此时乙种花卉种植面积为.
答:应分配甲种花卉种植面积为,乙种花卉种植面积为,才能使种植总费用最少,最少总费用为119000元. ………………………………10分
22.【详解】(1)解:∵方程的两根是、∴
∴∴; ………………………………………3分
(2)解:由(1)可知:,
…………………5分
∴(负值舍去); ……………………………………6分
(3)解:由题意可得新一元二次方程的两个根为和
则
……………………………………8分
……………………………………9分
所以新的一元二次方程. ……………………………………10分
23.【详解】(1)证明:如图,连接OD,
∵AD为∠BAC的角平分线,∴∠BAD=∠CAD, ……………………………………1分
∵OA=OD,∴∠ODA=∠OAD,∴∠ODA=∠CAD,∴OD∥AC,
∵∠C=90°,∴∠ODC=90°,∴OD⊥BC,∴BC为圆O的切线;………………………3分
(2)连接DF,由(1)知BC为圆O的切线,
∴∠FDC=∠DAF,
∴∠CDA=∠CFD,
∴∠AFD=∠ADB,
∵∠BAD=∠DAF,∴△ABD∽△ADF, ………………………………………5分
∴ ,即AD2=AB•AF=xy,则AD= ……………………………………6分
(3)连接EF,在Rt△BOD中,sinB=,
设圆的半径为r,可得,解得:r=5,∴AE=10,AB=18,…………………7分
∵AE是直径,∴∠AFE=∠C=90°,∴EF∥BC,∴∠AEF=∠B,∴sin∠AEF=,
∴AF=AE•sin∠AEF=10×, ……………………………………8分
∵AF∥OD,∴,即DG=AD,
∵AD=,则DG=×=.…………………10分
24.【详解】(1)∵在正方形ABCD中,AD∥BC,∴∠DAG=∠F,
又∵AG平分∠DAE,∴∠DAG=∠EAG,∴∠EAG=∠F,∴EA=EF,………………1分
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,∴AE==, ……………………………………2分
∴EF=,∴CF=EF﹣EC=﹣1; ……………………………………3分
(2)①证明:∵EA=EF,EG⊥AF,∴AG=FG, ……………………………………4分
在△ADG和△FCG中, ……………………………………5分
∴△ADG≌△FCG(AAS),∴DG=CG,即点G为CD的中点; ……………………6分
②设CD=2a,则CG=a,由①知,CF=DA=2a,
∵EG⊥AF,∠GDF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,∴△EGC∽△GFC,∴,………………………………………8分
∵GC=a,FC=2a,∴,∴,
∴EC=a,BE=BC﹣EC=2a﹣a=a,
∴λ=. …………………………………10分
25.【详解】(1)∵抛物线与轴交于,两点,与轴交于点.∴,∴, …………………………………2分
∴抛物线的函数表达式为; ………………………………………3分
(2)过点作轴于点,交于点,过点作轴交的延长线于点.
则DG//AK,∴△AEK∽△DEF,∴, ………………………………………4分
设直线BC的解析式为y=kx+n,
将、代入则有:,解得,…………………………5分
∴直线的表达式为,当x=-1时,,即K(-1,),∴.
∵.∴ ………………………………………6分
设点,则F点坐标为(m,),
∴.
∴,
当时,有最大值. ……………………………………7分
(3)∵,,.
∴AC=,BC=,AB=5,
∴AC2+BC2=25=52=AB2,∴∠ACB=90°,
∵过点作直线,直线的表达式为,
∴直线的表达式为.设点的坐标为.…………………………………8分
①当点在直线右侧时,如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,∴∠M=∠PNB=90°,
∴∠BPN+∠PBN=90°,
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°,
∴∠QPM=∠PBN,∴,∴,
又∵,∴,∴,…………………9分
∵NB=t-4,PN=,∴,∴QM=,PM=,
∴MN=+,,∴点的坐标为.
将点的坐标为代入,得
,解得:,t2=0(舍去),此时点的坐标为.
……10分
②当点在直线左侧时.如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,∴∠M=∠PNB=90°,∴∠BPN+∠PBN=90°,
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°,∴∠QPM=∠PBN,
∴,∴,又∵,∴,
∴, ……………………………………11分
∵NB=4-t,PN=,∴,∴QM=,PM=,
∴MN=+,,∴点的坐标为.
将点的坐标为代入,得
,解得:,
相关试卷
这是一份四川省阆中中学校2024~2025学年九年级(上)期中数学试卷(含答案),共10页。
这是一份2023-2024学年四川省成都七中育才学校九年级(下)月考数学试卷(含答案),共17页。试卷主要包含了选择题,非选择题等内容,欢迎下载使用。
这是一份四川省达州市第一中学校2023届九年级下学期第一次月考数学试卷(含答案),共6页。









