福建省厦门第十一中学2024-2025学年上学期八年级数学期中质量检测卷(无答案)

展开

这是一份福建省厦门第十一中学2024-2025学年上学期八年级数学期中质量检测卷(无答案)，共6页。试卷主要包含了请将答案正确填写在答题卡上，出一个三角形，以晾晒蜡染布等内容，欢迎下载使用。
（试卷满分：150分；考试时间：120分钟）
注意事项：
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题（本题共10小题，每小题4分，共40分.每小题都有四个选项，其中有且只有一个选项正确）
1．冬季奥林匹克运动会是世界规模最大的冬季综合性运动会，年北京冬奥会的声音是人类命运共同体的赞歌，是对“更快、更高、更强、更团结”的奥运精神的中国宣扬. 下列四个图分别是四届冬奥会图标中的一部分，其中是轴对称图形的为
A．B．
C．D．
2．下列运算正确的是
A．2a+3b=5abB．5a2-3a=2aC．(ab3)2=a2b6D．(a+2)2=a2+4
3．如图，四边形ABCD的对角线AC,BD交于点O,E是BC边上的一点，连接AE,OE，则下列角中是△AEO的外角的是
A．∠AEBB．∠AODC．∠OECD．∠EOC
4．到△ABC的三条边距离相等的点是△ABC的是
A．三条中线的交点B．三条角平分线的交点
C．三条高线的交点D．三条边的垂直平分线的交点
5．如图，工人师傅设计了一种测零件内径AB的卡钳，卡钳交叉点O为AA'、BB'的中点，只要量出A'B'的长度，就可以知道该零件内径AB的长度. 依据的数学基本事实是
A．两边及其夹角分别相等的两个三角形全等
B．两角及其夹边分别相等的两个三角形全等
C．两条直线被一组平行线所截，所得的对应线段成比例
D．两点之间线段最短
6．①在OA和OB上分别截取OC,OD，使OC=OD；
②分别以C,D为圆心，以大于12CD的长为半径作弧，两弧在∠AOB内交于点M；③作射线OM，连接CM,DM，如图所示.
根据以上作图，一定可以推得的结论是
A．∠1=∠2且CM=DMB．∠1=∠3且CM=DM
C．∠1=∠2且OD=DMD．∠3=∠2且OD=DM
7．已知a=1631,b=841,c=461，则a,b,c的大小关系是
A．a>b>cB．a>c>bC．aa
8．观察等式：2+22=23-2;2+22+23=24-2;2+22+23+24=25-2…已知按一定规律排列的一组数：250、251、252、…、299、2100.若250=a，用含a的式子表示这组数的和是（）
A．2a2-2aB．2a2-2a-2C．2a2-aD．2a2+a
9．如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕点A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是
A．AB=ANB．AB//NCC．∠AMN=∠ACND．MN⊥AC
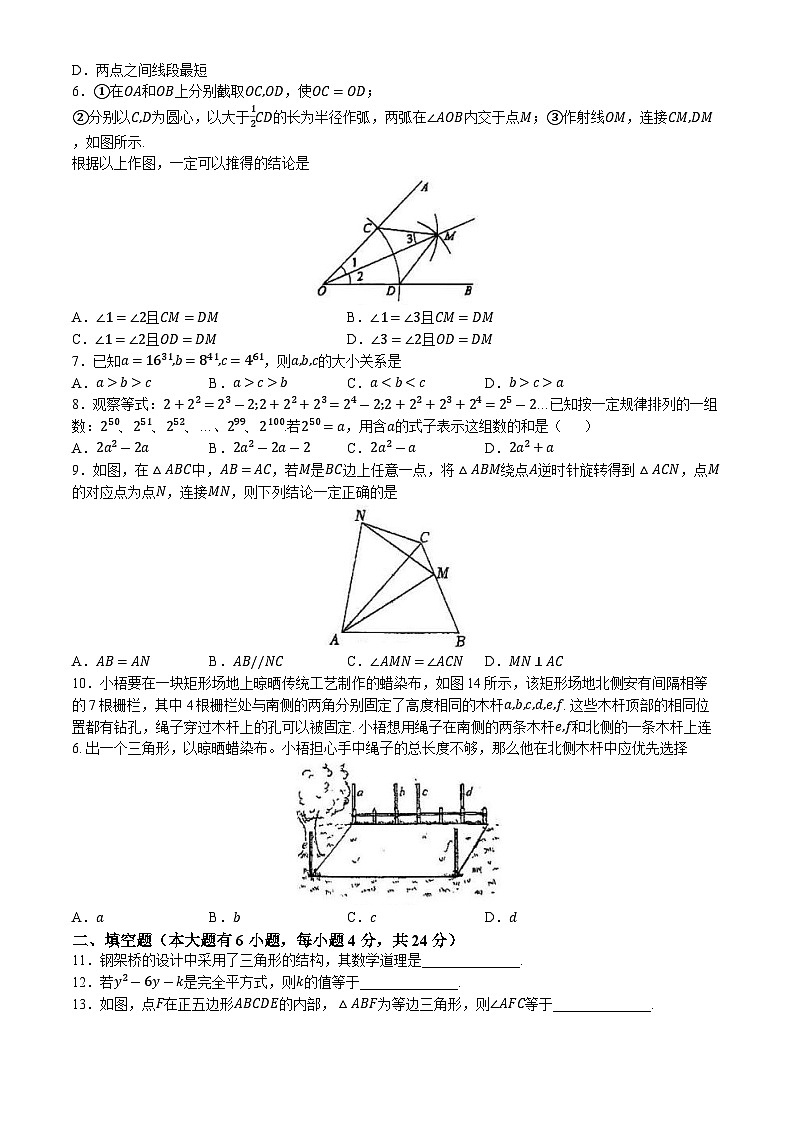
10．小梧要在一块矩形场地上晾晒传统工艺制作的蜡染布，如图14所示，该矩形场地北侧安有间隔相等的7根栅栏，其中4根栅栏处与南侧的两角分别固定了高度相同的木杆a,b,c,d,e,f. 这些木杆顶部的相同位置都有钻孔，绳子穿过木杆上的孔可以被固定. 小梧想用绳子在南侧的两条木杆e,f和北侧的一条木杆上连6. 出一个三角形，以晾晒蜡染布。小梧担心手中绳子的总长度不够，那么他在北侧木杆中应优先选择
A．aB．bC．cD．d
二、填空题（本大题有6小题，每小题4分，共24分）
11．钢架桥的设计中采用了三角形的结构，其数学道理是______________.
12．若y2-6y-k是完全平方式，则k的值等于______________.
13．如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC等于______________.
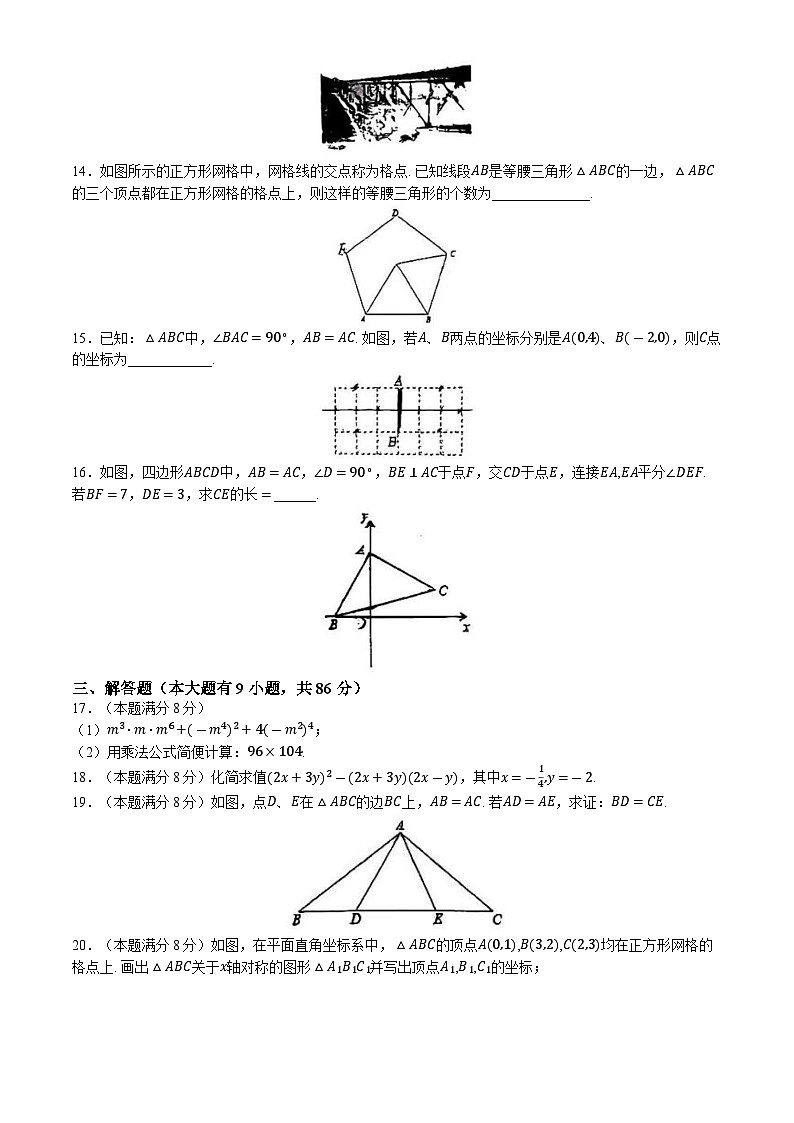
14．如图所示的正方形网格中，网格线的交点称为格点. 已知线段AB是等腰三角形△ABC的一边，△ABC的三个顶点都在正方形网格的格点上，则这样的等腰三角形的个数为______________.
15．已知：△ABC中，∠BAC=90∘，AB=AC. 如图，若A、B两点的坐标分别是A(0,4)、B(-2,0)，则C点的坐标为____________.
16．如图，四边形ABCD中，AB=AC，∠D=90∘，BE⊥AC于点F，交CD于点E，连接EA,EA平分∠DEF. 若BF=7，DE=3，求CE的长=______.
三、解答题（本大题有9小题，共86分）
17．（本题满分8分）
（1）m3⋅m⋅m6+(-m4)2+4(-m2)4；
（2）用乘法公式简便计算：96×104.
18．（本题满分8分）化简求值(2x+3y)2-(2x+3y)(2x-y)，其中x=-14,y=-2.
19．（本题满分8分）如图，点D、E在△ABC的边BC上，AB=AC. 若AD=AE，求证：BD=CE.
20．（本题满分8分）如图，在平面直角坐标系中，△ABC的顶点A(0,1),B(3,2),C(2,3)均在正方形网格的格点上. 画出△ABC关于x轴对称的图形△A1B1C1并写出顶点A1,B1,C1的坐标；
21．（本题满分8分）4张长为a、宽为b(a>b)的长方形纸片，按如图的方式拼成一个边长为(a+b)的正方形，图中空白部分的面积为S1，阴影部分的面积为S2.
（1）若a=3,b=1，则S1=____；
（2）若S1=2S2，求a与b满足关系.
22．（本题满分10分）第1个等式：(2×1+1)2=(2×2+1)2-(2×2)2
第2个等式：(2×2+1)2=(3×4+1)2-(3×4)2
第3个等式：(2×3+1)2=(4×6+1)2-(4×6)2
第4个等式：(2×4+1)2=(5×8+1)2-(5×8)2
……
按照以上规律，解决下列问题：
（1）写出第5个等式：________________________；
（2）写出你猜想的第n个等式（用含n的式子表示），并证明.
23．（本题满分10分）综合与实践：
问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第Ⅰ卷命题9“平分一个已知角，”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA和OB上分别取点C和D，使得OC=OD，连接CD，以CD为边作等边三角形CDE，则OE就是∠AOB的平分线. 请写出OE平分∠AOB的依据：______________；
类比迁移：（2）小明根据以上信息研究发现：△CDE不一定必须是等边三角形，只需CE=DE即可，他查阅资料；我国古代已经用角尺平分任意角，做法如下：如图3，在∠AOB的边OA,OB上分别取OM=ON，移动角尺，使角尺两边相同刻度分别与点M,N重合，则过角尺顶点C的射线OC是∠AOB的平分线，请说明此做法的理由；
拓展实践：（3）小明将研究应用于实践：如图4，校园的两条小路AB和AC，汇聚形成了一个岔路口A，现在学校要在两条小路之间安装一盏路灯E，使得路灯照亮两条小路（两条小路一样亮），并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等，试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置. （保留作图痕迹，不写作法）
24．（本题满分12分）将一个三角形沿着其中一个顶点及其对边上的一点所在的直线折叠，若折叠后原三角形的一边垂直于这条对边，则称这条直线是该三角形的“对垂线”.
（1）如图1，AD是等边△ABC的对垂线，把△ABC沿直线AD折叠后，点B落在点B'处，求∠BAD的度数；
（2）如图2，在△ABC中，∠BAC=90∘，点D在边BC上，且AB=AD，若∠B=2∠DAC，判断直线AD是否是△ABC的对垂线，并说明理由.
25．（本题满分14分）已知线段AB和点C,CA=CD,CB=CE,∠DCA=∠ECB，AE,BD相交于点P.
（1）如图1，若点C在线段AB上，
①求证：∠A=∠D；
②若∠DCA=60∘，求∠DPA的度数；
（2）如图2，点C是线段AB上方的一点，且保持∠DCA=60∘，连接PC。请问PC、PA、PD之间有什么关系？请证明。