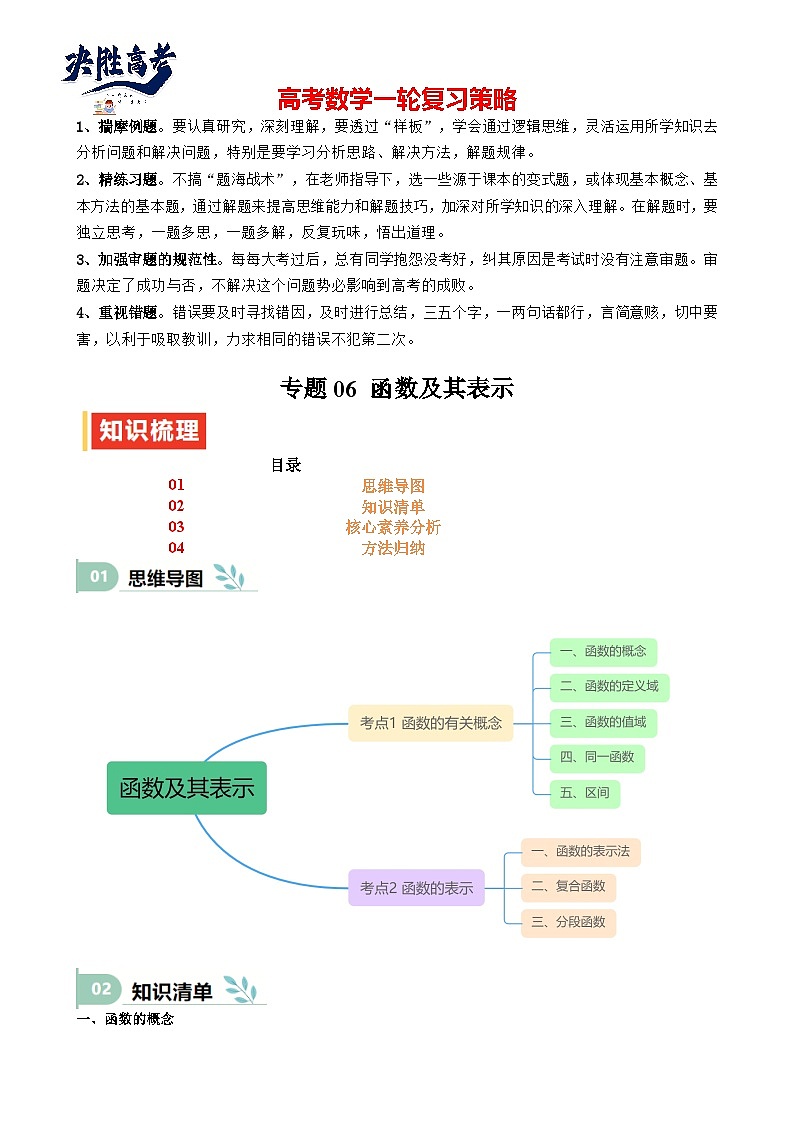
专题06 函数及其表示（七大题型+模拟精练+核心素养分析+方法归纳）-2025年高考数学一轮复习 （新高考专用）

这是一份专题06 函数及其表示（七大题型+模拟精练+核心素养分析+方法归纳）-2025年高考数学一轮复习 （新高考专用），文件包含专题06函数及其表示思维导图+知识清单+核心素养分析+方法归纳原卷版docx、专题06函数及其表示七大题型+模拟精练原卷版docx、专题06函数及其表示七大题型+模拟精练解析版docx等3份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
2、精练习题。不搞“题海战术”，在老师指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题06 函数及其表示
一、函数的概念
1.函数的定义
设A,B 是非空的数集，如果按照某种确定的对应关系 f,使对于集合A中的任意一个数x, 在集合B 中都有唯一确定的数 f(x)和它对应，那么就称 f:A→B为从集合A到集合B的一个函数，记作y =f(x),x∈A.其中，x 叫做自变量，x 的取值范围A 叫做函数的定义域.显然，值域是集合 B 的子集.
2.函数的构成要素
函数的构成要素为：定义域、对应关系和值域.三者缺一不可，其中对应关系是核心，定义域是根本，当定义域和对应关系确定了，值域也就确定了.
二、函数的定义域
1.函数的定义域是自变量x的取值集合，它是函数的重要组成部分.
2.求函数定义域的注意事项
(1)分式的分母不为0;
(2)偶次根式的被开方数大于等于0;
(3)零次幂的底数不为0;
(4)实际问题中自变量的范围；
(5)多个式子构成的函数，其定义域要满足每个式子都有意义.
三、函数的值域
1.函数的值域是在对应关系 f 的作用下，自变量x在定义域内取值时相应的函数值组成的集合目录
01
思维导图
02
知识清单
03
核心素养分析
04
方法归纳
四、同一个函数
如果两个函数的定义域相同，并且对应关系完全一致，即相同的自变量对应的函数值也相同，那么这两个函数是同一个函数.
温馨提示：当一个函数的对应关系和定义域确定后，其值域就随之确定，所以两个函数当且仅当定义城和对应关系相同时，才为同一函数.换言之，(1)定义域不同，两函数不同；(2)值域不同，两函数不同；(3)对应关系不同，两函数不同，即使定义域和值城分别相同的两个函数，也不一定是同一函数，如y=5x 与它们的定义域和值域都是实数集R, 但不是同一个函数.
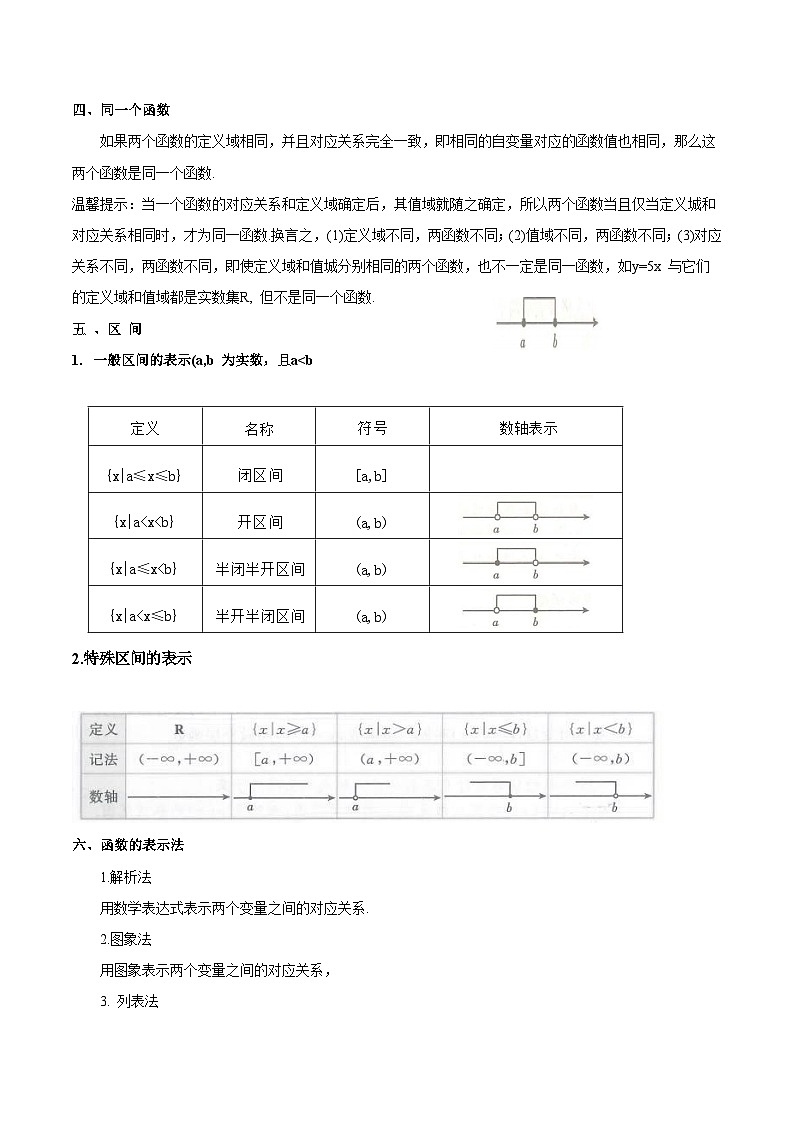
五 、区 间
一般区间的表示(a,b 为实数，且a0，,x＋1≠1，,4－x2≥0，))
解得－10，,x2＋6x≥0，))
解得x>2或x≤－6.
因此函数的定义域为(－∞，－6]∪(2，＋∞)．
2．已知函数f(x)＝eq \f(x,\r(1－2x))，则函数eq \f(fx－1,x＋1)的定义域为( )
A．(－∞，1)
B．(－∞，－1)
C．(－∞，－1)∪(－1,0)
D．(－∞，－1)∪(－1,1)
答案 D
解析 令1－2x>0，
即2x1)．
(2)已知y＝f(x)是二次函数，若方程f(x)＝0有两个相等实根，且f′(x)＝2x＋2，则f(x)＝________.
答案 x2＋2x＋1
解析 设f(x)＝ax2＋bx＋c(a≠0)，
则f′(x)＝2ax＋b，∴2ax＋b＝2x＋2，
则a＝1，b＝2.∴f(x)＝x2＋2x＋c，
又f(x)＝0，
即x2＋2x＋c＝0有两个相等实根．
∴Δ＝4－4c＝0，则c＝1.
故f(x)＝x2＋2x＋1.
(3)已知函数对任意的x都有f(x)－2f(－x)＝2x，则f(x)＝________.
答案 eq \f(2,3)x
解析 ∵f(x)－2f(－x)＝2x，①
∴f(－x)－2f(x)＝－2x，②
由①②得f(x)＝eq \f(2,3)x.
拓展
已知f(x)满足f(x)－2f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))＝2x，则f(x)＝________.
答案 －eq \f(2x,3)－eq \f(4,3x)
解析 ∵f(x)－2f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))＝2x，①
以eq \f(1,x)代替①中的x，得f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))－2f(x)＝eq \f(2,x)，②
①＋②×2得－3f(x)＝2x＋eq \f(4,x)，
∴f(x)＝－eq \f(2x,3)－eq \f(4,3x).
方法归纳： 函数解析式的求法
(1)配凑法；(2)待定系数法；(3)换元法；(4)解方程组法．
三、分段函数
例3 (1)已知f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(cs πx，x≤1，,fx－1＋1，x>1，))则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)))＋f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,3)))的值为( )
A.eq \f(1,2) B．－eq \f(1,2) C．－1 D．1
答案 D
解析 f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)))＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)－1))＋1＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))＋1
＝cs eq \f(π,3)＋1＝eq \f(3,2)，
f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,3)))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4π,3)))
＝cs eq \f(2π,3)＝－eq \f(1,2)，
∴f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)))＋f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4,3)))＝eq \f(3,2)－eq \f(1,2)＝1.
(2)已知f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋3，x>0，,x2－4，x≤0，))若f(a)＝5，则实数a的值是__________；若f(f(a))≤5，则实数a的取值范围是__________．
答案 1或－3 [－eq \r(5)，－1]
解析 ①当a>0时，2a＋3＝5，解得a＝1；
当a≤0时，a2－4＝5，
解得a＝－3或a＝3(舍)．
综上，a＝1或－3.
②设t＝f(a)，由f(t)≤5得－3≤t≤1.
由－3≤f(a)≤1，解得－eq \r(5)≤a≤－1.
拓展
1．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(sin\b\lc\(\rc\)(\a\vs4\al\c1(πx＋\f(π,6)))，x>1，,\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x，x