





所属成套资源:【备战2025】高考数学一轮复习【高考仿真训练+特训+专题突破+月考】(新高考专用)
- 专题10 三角函数的概念 诱导公式(七大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用) 试卷 0 次下载
- 专题11 三角恒等变换及应用(八大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用) 试卷 0 次下载
- 专题13 导数的概念及运算(九大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用) 试卷 0 次下载
- 专题14 导数与函数的单调性(九大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用) 试卷 0 次下载
- 专题15 导数与函数的极值、最值(十一大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用) 试卷 0 次下载
专题12 三角函数的图像与性质(七大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用)
展开
这是一份专题12 三角函数的图像与性质(七大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用),文件包含专题12三角函数的图像与性质思维导图+知识清单+核心素养分析+方法归纳原卷版docx、专题12三角函数的图像与性质七大题型+模拟精练原卷版docx、专题12三角函数的图像与性质七大题型+模拟精练解析版docx等3份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。
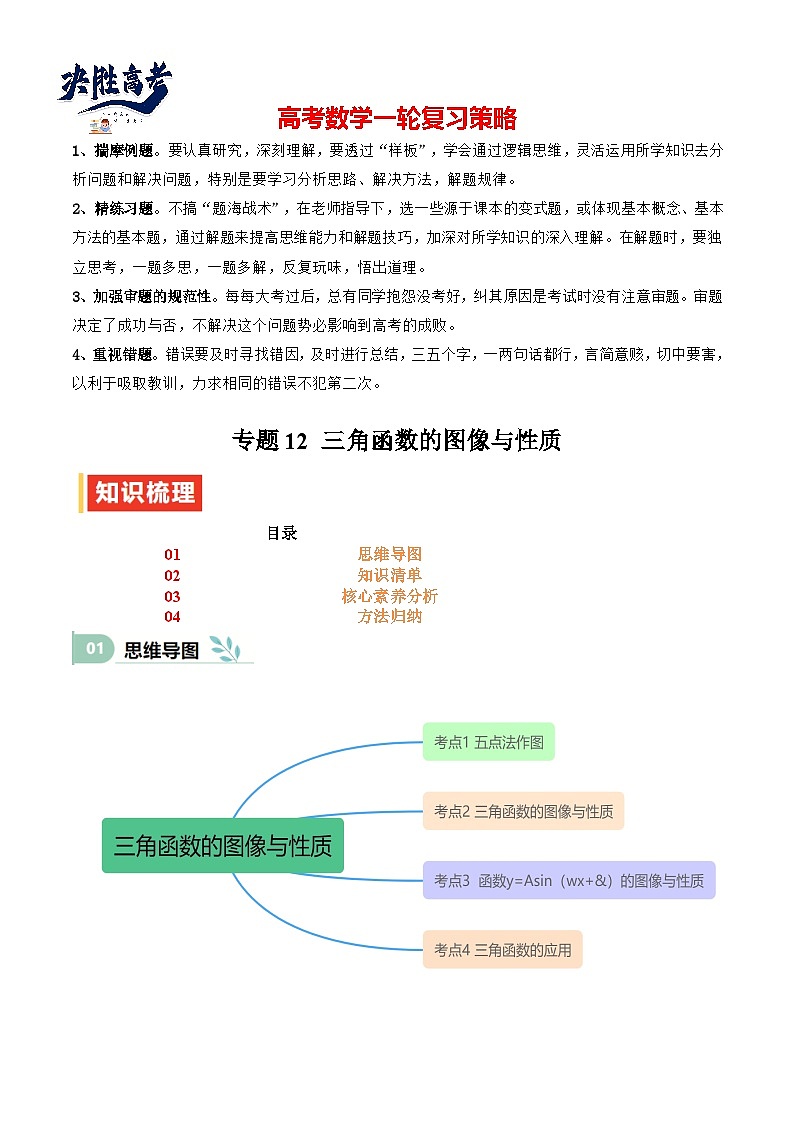
2、精练习题。不搞“题海战术”,在老师指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
专题12 三角函数的图像与性质(七大题型+模拟精练)
目录:
01 求三角函数的有关概念
02 三角函数图像的变换
03 识别函数图像、根据已知图像求解
04 三角函数图像与性质的综合辨析
05 三角函数性质的综合应用—求参数范围或最值
06 三角函数的应用
07 三角函数的综合解答题
01 求三角函数的有关概念
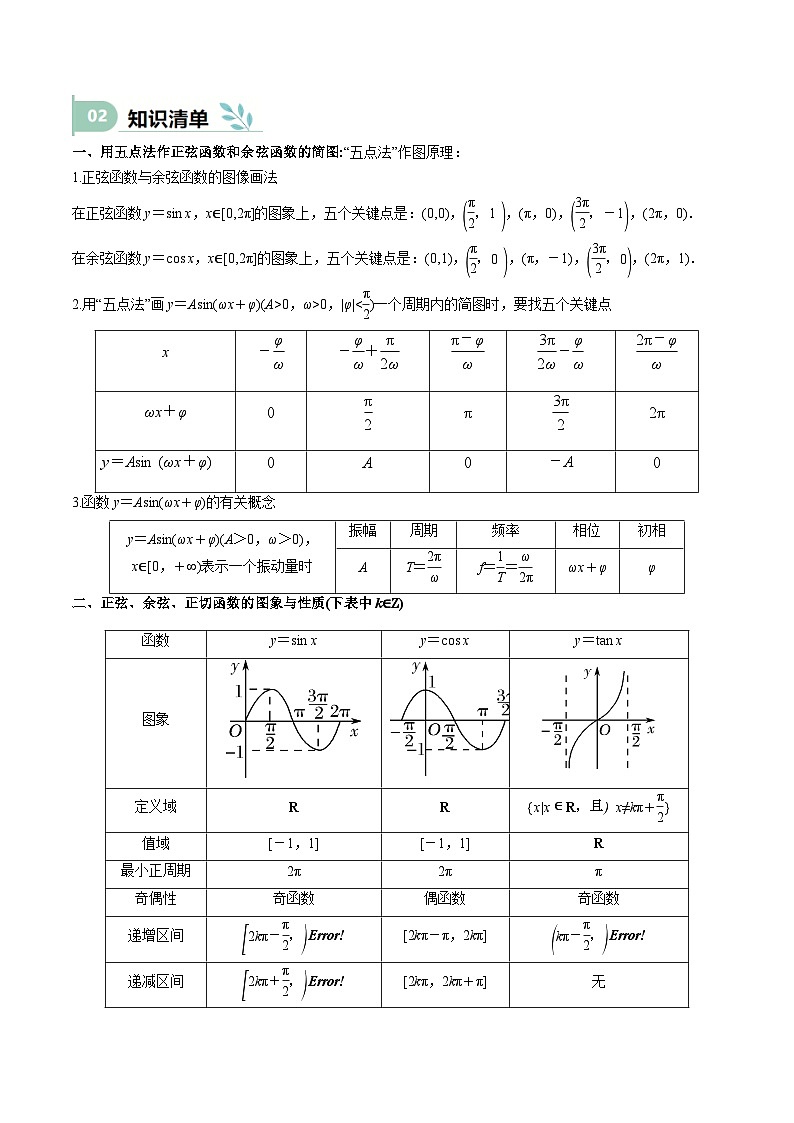
1.(2024高三·全国·专题练习)函数的最小正周期是 .
2.(2023高三·全国·专题练习)y=cs的单调递减区间为 .
3.(23-24高一下·山东威海·阶段练习)已知函数,的图象的对称中心是 .
4.(2024·贵州黔南·二模)若函数为偶函数,则的值可以是( )
A.B.C.D.
5.(2024高三·全国·专题练习)下列函数中,以π为周期,且在区间上单调递增的是( )
A.B.C.D.
6.(23-24高一下·重庆·阶段练习)下列函数中,周期为且在上单调递增的函数是( )
A.B.
C.D.
7.(2024高三·全国·专题练习)若函数y=cs (3x+φ)的图象关于原点成中心对称,则φ= .
8.(23-24高二上·湖南长沙·期末)函数的部分图像如图所示,则其解析式为( )
A.B.
C.D.
9.(2024高三上·全国·专题练习)函数,的值域为 .
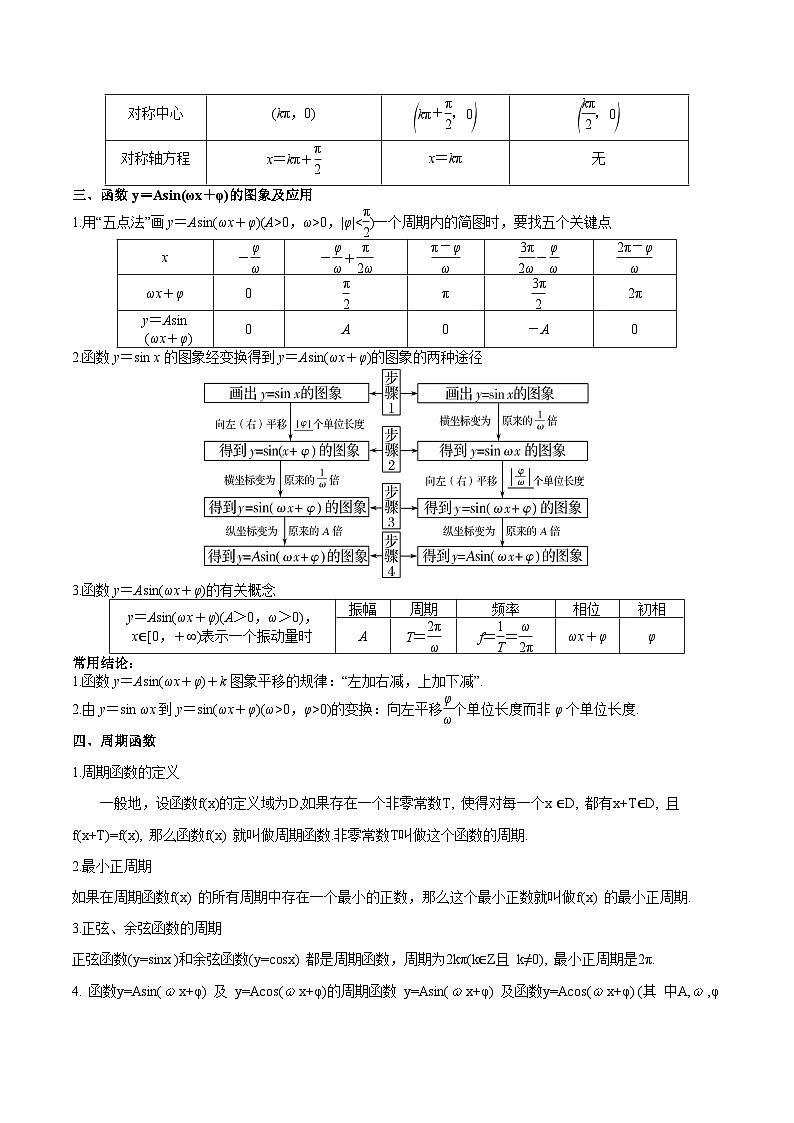
02 三角函数图像的变换
10.(23-24高一下·广东佛山·期中)为了得到的图像,需要把函数的图象向右平移的单位数是( )
A.B.C.D.
11.(23-24高一下·四川·期中)的图象如图所示,为了得到的图象,则只要将的图象( )
A.向右平移个单位长度B.向右平移个单位长度
C.向左平移个单位长度D.向左平移个单位长度
12.(23-24高一下·四川绵阳·阶段练习)为了得到函数的图象,只需要把函数图象( )
A.先将橫坐标缩短到原来的倍(纵坐标不变),再向右平移个单位
B.先将横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位
C.先向左平移个单位,再将横坐标伸长到原来的2倍(纵坐标不变)
D.先向右平移个单位,再将横坐标伸长到原来的2倍(纵坐标不变)
13.(23-24高三上·辽宁抚顺·期末)先将函数图象上所有点的横坐标缩短为原来的(纵坐标不变),再把得到的曲线向左平移个单位长度,得到函数的图象,写出图象的一条对称轴的方程: .
14.(2024·陕西榆林·三模)将函数的图象向左平移个单位长度后得到的函数图象关于对称,则实数的最小值为( )
A.B.C.D.
03 识别函数图像、根据已知图像求解
15.(2024·全国·模拟预测)函数的图像大致是( )
A. B. C. D.
16.(2024·吉林长春·模拟预测)已知函数,如图是直线与曲线的两个交点,,则( )
A.0B.C.D.
17.(2024·江西南昌·一模)函数的部分图象如图所示,是等腰直角三角形,其中两点为图象与轴的交点,为图象的最高点,且,则( )
A.B.
C.D.
18.(2024·广东广州·二模)已知函数的部分图象如图所示,若将函数的图象向右平移个单位后所得曲线关于轴对称,则的最小值为( )
A.B.C.D.
04 三角函数图像与性质的综合辨析
19.(2024高三·全国·专题练习)已知函数,则( )
A.的最小值为2B.的图象关于y轴对称
C.的图象关于直线对称D.的图象关于直线对称
20.(2024·四川·模拟预测)已知函数的最小正周期为,下列结论中正确的是( )
A.函数的图象关于对称
B.函数的对称中心是
C.函数在区间上单调递增
D.函数的图象可以由的图象向右平移个单位长度得到
21.(2024·陕西渭南·二模)关于函数,给出如下结论:
①的图象关于点对称
②的图象关于直线对称
③的最大值是3
④是函数的周期
其中正确结论的个数为( )
A.1B.2C.3D.4
05 三角函数性质的综合应用—求参数范围或最值
22.(2024·河北唐山·二模)函数在上为单调递增函数,则的取值范围为( )
A.B.C.D.
23.(2024·安徽马鞍山·三模)已知函数的一个零点是,且在上单调,则( )
A.B.C.D.
24.(2024·四川内江·三模)设函数,若存在,且,使得,则的取值范围是( )
A.B.C.D.
25.(2024·江苏南通·二模)已知函数()在区间上单调递增,则的最大值为( )
A.B.C.D.
26.(2024·全国·模拟预测)已知函数,对于任意的,,都恒成立,且函数在上单调递增,则的值为( )
A.3B.9C.3或9D.
27.(2024·陕西安康·模拟预测)将函数的图象向左平移个单位长度,再将所得函数图象上所有点的横坐标变为原来的倍,纵坐标不变,得到函数的图象,若函数在上有5个零点,则的取值范围是( )
A.B.C.D.
06 三角函数的应用
28.(2024·四川凉山·三模)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近位置进仓,转一周大约需要30min.某游客坐上摩天轮的座舱10min后距离地面高度约为( )
A.92.5mB.87.5mC.82.5mD.
29.(2023·全国·模拟预测)随着电力的发展与石油的消耗,风力发电越来越受到重视.预计到2025年全球风电新增装机量达到111.2GW,中国的装机量占比达到世界第一.已知风速稳定时风力发电机叶片围绕转轴中心做匀速圆周运动,现有两个风力发电机,和分别为两个风力发电机叶片边缘一点,和到各自转轴中心距离均为20米,初始时刻处于所在的发电机转轴中心正上方,处于所在的发电机转轴中心正下方,且和围绕各自发电机转轴中心做匀速圆周运动.由于两个发电机所处位置风速不同,点转速为,点转速为,以时间(单位:秒)为自变量,和与各自发电机转轴中心高度差为应变量,分别得三角函数与,下列哪种方式可以使变为( )
A.将图象上所有点向右平移个单位长度,再将横坐标扩大到原来的倍
B.将图象上所有点向左平移个单位长度,再将横坐标缩小到原来的倍
C.将图象上所有点的横坐标扩大到原来的倍,再向左平移个单位长度
D.将图象上所有点的横坐标缩小到原来的倍,再向右平移个单位长度
30.(22-23高三上·安徽亳州·阶段练习)某杂技表演是在一种转轮状的机械上完成,表演者站在转轮的固定板上慢慢往上转的同时完成各种表演.转轮模型如图.已知转轮最高点距离地面高度为11米,转轮半径为5米,转轮上设置了8个固定板.开启后按逆时针方向匀速旋转,转一周大约要5分钟.若甲、乙两位表演者在相邻的两个固定板上表演,在运行一周的过程中,求两人距离地面的高度差的最大值为( )
A.B.
C.D.
07 三角函数的综合解答题
31.(2024·山西临汾·三模)已知函数的图象可由函数的图象平移得到,且关于直线对称.
(1)求的值;
(2)求函数的单调递增区间.
32.(2023·四川绵阳·模拟预测)已知函数满足.
(1)求函数的解析式及最小正周期;
(2)函数的图象是由函数的图象向左平移个单位长度得到,若,求的最小值.
33.(2023·海南省直辖县级单位·模拟预测)如图为函数的部分图象,且,.
(1)求,的值;
(2)将的图象上所有点的横坐标扩大到原来的3倍(纵坐标不变),再向右平移个单位长度,得到函数的图象,讨论函数在区间的零点个数.
34.(21-22高一下·山东临沂·阶段练习)已知函数,其图象中相邻的两个对称中心的距离为,且函数的图象关于直线对称;
(1)求出的解析式;
(2)将的图象向左平移个单位长度,得到曲线,若方程在上有两根,,求的值及的取值范围.
35.(2022·河南濮阳·模拟预测)已知函数,将的图象向右平移个单位长度,再将所有点的横坐标伸长为原来的2倍,纵坐标不变,得到函数的图象.
(1)求的解析式;
(2)若函数,求在区间上的所有最大值点.
一、单选题
1.(2024·安徽·三模)“”是“函数的图象关于对称”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
2.(2024·广东湛江·二模)函数在上的值域为( )
A.B.C.D.
3.(2024·四川绵阳·三模)若函数的图象关于直线对称,在下列选项中,( )不是的零点
A.B.C.D.
4.(2024·全国·二模)若函数的图象关于轴对称,则( )
A.B.C.D.
5.(2024·四川德阳·二模)函数的图象大致是( )
A.B.
C.D.
6.(2024·山西·模拟预测)方程的实数根的个数为( )
A.9B.10C.11D.12
7.(2024·河南三门峡·模拟预测)已知函数的部分图象如图所示,将的图象向左平移个单位长度后得到函数的图象,若在区间上的值域为,则的取值范围为( )
A.B.C.D.
8.(2024·天津红桥·一模)将函数的图象横坐标伸长为原来的2倍,再向左平移单位,得到函数的部分图象(如图所示).对于,,且,若,都有成立,则下列结论中不正确的是( )
A.
B.
C.在上单调递增
D.函数在的零点为,则
二、多选题
9.(2024·湖南·模拟预测)已知函数的图象经过点,则下列结论正确的是( )
A.函数的最小正周期为
B.
C.函数的图象关于点中心对称
D.函数在区间单调递减
10.(2024·全国·模拟预测)已知函数的图象过点,且两条相邻对称轴之间的距离为,则下列说法正确的是( )
A.
B.在上单调递增
C.直线为函数图象的一条对称轴
D.在上的值域为
11.(2023·山东·模拟预测)已知函数图象的一条对称轴为直线,函数,则( )
A.将的图象向左平移个单位长度得到的图象
B.方程的相邻两个实数根之差的绝对值为
C.函数在区间上单调递增
D.在区间上的最大值与最小值之差的取值范围为
三、填空题
12.(2024·湖北武汉·二模)函数的部分图象如图所示,则 .
13.(2024·湖南衡阳·模拟预测)已知函数图象过点,则 ;若函数的图象关于点中心对称,则 .
14.(2024·北京朝阳·二模)设为正整数,已知函数,,. 当时,记,其中. 给出下列四个结论:
①,;
②,;
③若,则;
④若,则.
其中所有正确结论的序号是 .
四、解答题
15.(2023·吉林长春·模拟预测)已知函数(,,)的部分图象如图所示.
(1)求的解析式;
(2)设,若函数在区间上单调递增,求实数的最大值.
16.(2024·山西临汾·三模)已知函数的图象可由函数的图象平移得到,且关于直线对称.
(1)求的值;
(2)求函数的单调递增区间.
17.(2023·辽宁朝阳·模拟预测)已知函数(其中,,均为常数,,,).在用五点法作出函数在某一个周期的图像时,列表并填入了部分数据,如表所示:
(1)求函数的解析式,并直接写出函数的单调递增区间;
(2)已知函数满足,若当函数的定义域为()时,其值域为,求的最大值与最小值.
18.(2023·安徽亳州·模拟预测)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象向左平移个单位,得到函数的图象,若方程在上有解,求实数的取值范围.
0
0
相关试卷
这是一份专题26 双曲线(七大题型 模拟精练 核心素养分析 方法归纳)-2025年高考数学一轮复习 (新高考专用),文件包含专题26双曲线七大题型模拟精练核心素养分析方法归纳原卷版docx、专题26双曲线七大题型模拟精练核心素养分析方法归纳解析版docx、专题26双曲线七大题型模拟精练核心素养分析方法归纳docx等3份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
这是一份专题25 椭圆(七大题型 模拟精练 核心素养分析 方法归纳)-2025年高考数学一轮复习 (新高考专用),文件包含专题25椭圆七大题型模拟精练核心素养分析方法归纳-新高考专用专题25椭圆七大题型模拟精练原卷版docx、专题25椭圆七大题型模拟精练核心素养分析方法归纳-新高考专用专题25椭圆七大题型模拟精练解析版docx、专题25椭圆七大题型模拟精练核心素养分析方法归纳-新高考专用专题25椭圆思维导图知识清单核心素养分析方法归纳docx等3份试卷配套教学资源,其中试卷共64页, 欢迎下载使用。
这是一份专题24 直线和圆的方程(七大题型+模拟精练+核心素养分析+方法归纳)-2025年高考数学一轮复习 (新高考专用),文件包含专题24直线和圆的方程七大题型+模拟精练原卷版docx、专题24直线和圆的方程七大题型+模拟精练解析版docx、专题24直线和圆的方程思维导图+知识清单+核心素养分析+方法归纳docx等3份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。








