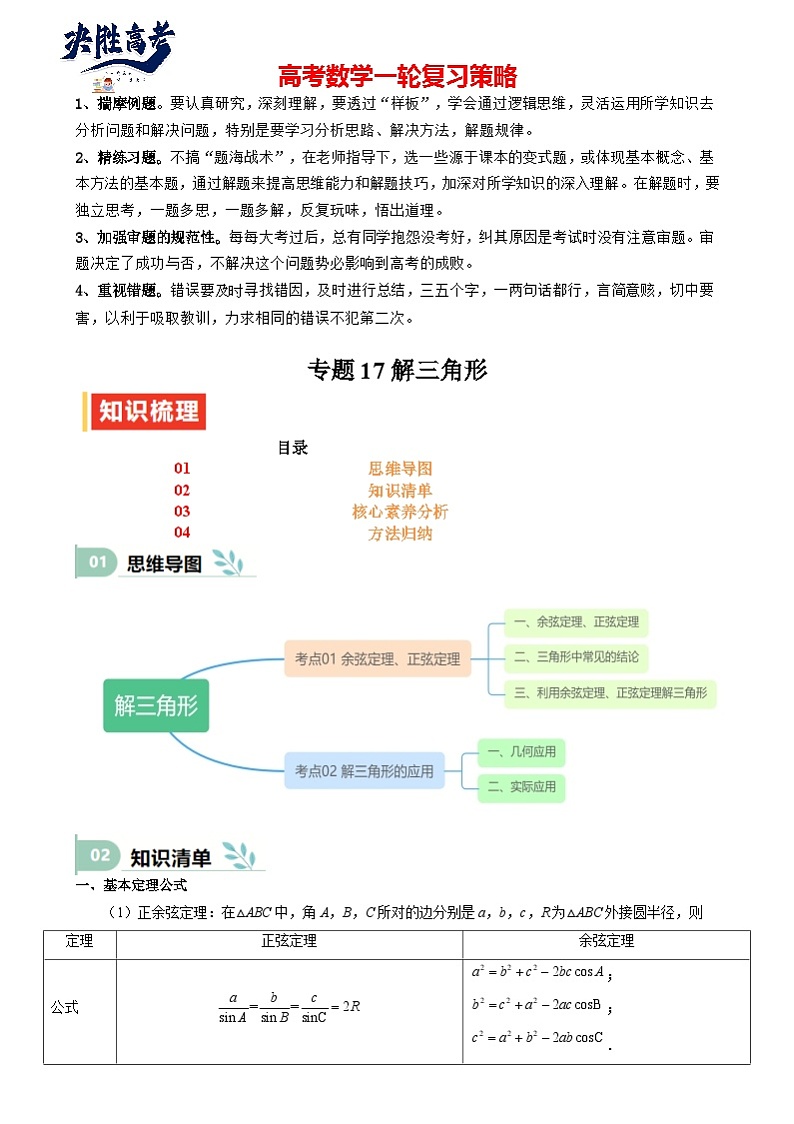
专题17 解三角形（七大题型 模拟精练 核心素养分析 方法归纳）-2025年高考数学一轮复习 （新高考专用）

这是一份专题17 解三角形（七大题型 模拟精练 核心素养分析 方法归纳）-2025年高考数学一轮复习 （新高考专用），文件包含专题17解三角形七大题型模拟精练核心素养分析方法归纳专题17解三角形七大题型模拟精练原卷版docx、专题17解三角形七大题型模拟精练核心素养分析方法归纳专题17解三角形七大题型模拟精练解析版docx、专题17解三角形七大题型模拟精练核心素养分析方法归纳专题17解三角形思维导图知识清单核心素养分析方法归纳docx等3份试卷配套教学资源，其中试卷共53页， 欢迎下载使用。
2、精练习题。不搞“题海战术”，在老师指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题17 解三角形（七大题型+模拟精练）
目录：
01 余弦定理、正弦定理
02 判断三角形的形状
03 解三角形与平面向量
04 解三角形几何的应用
05 取值范围、最值问题
06 解三角形的实际应用
07 解三角形解答题
01 余弦定理、正弦定理
1．（2024·浙江金华·三模）在中，角的对边分别为，，.若，，，则为（ ）
A．1B．2C．3D．1或3
2．（21-22高一下·江苏连云港·期中）△ABC的内角A，B，C的对边分别为a，b，c，已知，，，则（ ）
A．B．C．3D．
3．（2022·河南·模拟预测）已知的内角A，B，C的对边分别为a，b，c，面积为，，，则（ ）
A．B．5C．8D．
4．（2022·山西晋城·三模）的内角A，B，C的对边分别为a，b，c，已知，
则的面积为（ ）
A．B．C．1D．2
5．（2023·四川南充·三模）在中，角的对边分别是，若，则（ ）
A．B．C．D．
02 判断三角形的形状
6．（21-22高二上·广西桂林·期末）内角A，B，C的对边分别为a，b，c．若，则一定是（ ）
A．等腰三角形B．等边三角形
C．直角三角形D．等腰直角三角形
7．（2023·上海嘉定·一模）已知，那么“”是“为钝角三角形”的（ ）
A．充分条件但非必要条件B．必要条件但非充分条件
C．充要条件D．以上皆非
8．（2023·贵州·一模）在中，分别为角的对边，且满足，则的形状为（ ）
A．直角三角形B．等边三角形
C．直角三角形或等腰三角形D．等腰直角三角形
03 解三角形与平面向量
9．（2024·江苏盐城·模拟预测）中，若，则（ ）
A．54B．27C．9D．
10．（2024·安徽六安·模拟预测）已知平面向量，，满足，，，，则的最大值等于（ ）
A．B．C．D．
11．（2024·广东东莞·模拟预测）已知在同一平面内的三个点A，B，C满足，，则的取值范围是（ ）
A．B．C．D．
04 解三角形几何的应用
12．（2024·北京·三模）在四棱锥中，底面为正方形，，，，则的周长为（ ）
A．10B．11C．D．12
13．（2024·广东广州·模拟预测）在中，角、、的对边分别为、、，若，，的平分线的长为，则边上的中线的长等于（ ）
A．B．C．D．
14．（2023·四川南充·二模）在中，a，b，c分别是角A，B，C的对边，若，则的值为（ ）
A．2021B．2022C．2023D．2024
05 取值范围、最值问题
15．（2024·江苏连云港·模拟预测）在中，角A，B，C的对边分别为a，b，c，若，，则边b的取值范围为（ ）
A．B．C．D．
16．（2024·四川成都·模拟预测）设锐角的三个内角的对边分别为，且，则的取值范围为 （ ）
A．B．C．D．
17．（2024·河南·三模）在中，角A，B，C所对的边分别为a，b，c．若，则的最小值是（ ）
A．B．C．D．4
18．（2023·陕西榆林·一模）的内角所对的边分别为，若，则的取值范围为（ ）
A．B．C．D．
06 解三角形的实际应用
19．（2024·陕西西安·模拟预测）在高的楼顶处，测得正西方向地面上两点与楼底在同一水平面上）的俯角分别是和，则两点之间的距离为（ ）．
A．B．C．D．
20．（2024·广东·二模）在一堂数学实践探究课中，同学们用镜而反射法测量学校钟楼的高度.如图所示，将小镜子放在操场的水平地面上，人退后至从镜中能看到钟楼顶部的位置，此时测量人和小镜子的距离为，之后将小镜子前移，重复之前的操作，再次测量人与小镜子的距离为，已知人的眼睛距离地面的高度为，则钟楼的高度大约是（ ）

A．B．C．D．
21．（2024·上海嘉定·二模）嘉定某学习小组开展测量太阳高度角的数学活动．太阳高度角是指某时刻太阳光线和地平面所成的角．测量时，假设太阳光线均为平行的直线，地面为水平平面．如图，两竖直墙面所成的二面角为120°，墙的高度均为3米．在时刻，实地测量得在太阳光线照射下的两面墙在地面的阴影宽度分别为1米、1.5米．在线查阅嘉定的天文资料，当天的太阳高度角和对应时间的部分数据如表所示，则时刻最可能为（ ）
太阳高度角
时间
太阳高度角
时间
43.13°
08:30
68.53°
10:30
49.53°
09:00
74.49°
11:00
A．B．C．D．
22．（2024·云南昆明·一模）早期天文学家常采用“三角法”测量行星的轨道半径．假设一种理想状态：地球E和某小行星M绕太阳S在同一平面上的运动轨道均为圆，三个星体的位置如图所示．地球在位置时，测出；行星M绕太阳运动一周回到原来位置，地球运动到了位置，测出，．若地球的轨道半径为R，则下列选项中与行星M的轨道半径最接近的是（参考数据：）（ ）

A．B．C．D．
07 解三角形解答题
23．（2024·内蒙古·三模）在中，内角的对边分别为，且.
(1)求的值；
(2)若，证明：为直角三角形.
24．（2024·四川绵阳·模拟预测）三角形三内角，，的对边分别为，，.已知.
(1)求角的大小；
(2)若的面积等于，为边的中点，当中线的长最短时，求边的长.
25．（2024·重庆渝中·模拟预测）已知的内角的对边分别为，且满足.
(1)求角的大小；
55.93°
09:30
79.60°
11:30
62.29°
10:00
82.00°
12:00
(2)若为锐角三角形且，求面积的取值范围.
26．（2024·江西·模拟预测）在中，角，，所对的边分别记为，，，且．
(1)若，求的大小．
(2)若，求的取值范围．
27．（2023·全国·模拟预测）记△ABC的内角A，B，C的对边分别为a，b，c，已知．
(1)若，求A；
(2)若△ABC为锐角三角形，求的取值范围．
一、单选题
1．（2024·湖南·模拟预测）在中，，，，则（ ）
A．B．C．D．
2．（2024·吉林·模拟预测）在中，角A，B，C所对的边分别为a，b，c，“ ”是“”（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
3．（2024·江西九江·三模）在中，角所对的边分别为，已知，则（ ）
A．B．C．D．
4．（2024·陕西安康·模拟预测）在中，三个内角，，所对的边分别为，，，且，若，，则（ ）
A．1B．2C．D．4
5．（2024·浙江绍兴·三模）在中，内角A，B，C所对的边分别为a，b，c．若，则A等于（ ）
A．B．C．D．
6．（2024·重庆·模拟预测）记的内角的对边分别为，若，则的面积为（ ）
A．B．C．D．
7．（2024·湖北武汉·模拟预测）在三角形中，角，，的对边分别为，，且满足，，则面积取最大值时，（ ）
A．B．C．D．
8．（2024·全国·模拟预测）在锐角中，若，且，则能取到的值有（ ）
A．5B．4C．D．3
二、多选题
9．（2023·安徽·模拟预测）在中，，若满足条件的三角形有两个，则边的取值可能是（ ）
A．1.5B．1.6C．1.7D．1.8
10．（2024·江苏南京·二模）已知内角，，的对边分别为，，，为的重心，，，则（ ）
A．B．
C．的面积的最大值为D．的最小值为
11．（2024·贵州黔南·二模）已知锐角的三个内角，，的对边分别是，，，且的面积为.则下列说法正确的是（ ）
A．
B．的取值范围为
C．若，则的外接圆的半径为2
D．若，则的面积的取值范围为
三、填空题
12．（2024·湖南长沙·二模）在中，若，，，则 .
13．（2024·湖北襄阳·模拟预测）在中，，点D在线段上，，，，点M是外接圆上任意一点，则最大值为 .
14．（2024·江苏·模拟预测）在中，角所对的边分别为，若分别在边和上，且把的面积分成相等的两部分，则的最小值为 .
四、解答题
15．（2024·河北秦皇岛·三模）在中，内角，，所对的边分别为，，，且，的外接圆半径为.
(1)求的面积；
(2)求边上的高.
16．（2024·四川南充·模拟预测）在中，.
(1)求；
(2)若，求周长的最大值.
17．（2024·陕西西安·模拟预测）如图，在平面四边形中，，，的角平分线与相交于点，且.
(1)求的大小；
(2)求的值.
18．（2022·河南濮阳·模拟预测）在中,内角A,B,C的对边分别为a,b,c,已知
．
(1)求;
(2)若,D为边AC上一点,且．求的值．
19．（2024·河北·二模）若内一点满足，则称点为的布洛卡点，为的布洛卡角．如图，已知中，，，，点为的布洛卡点，为的布洛卡角．
(1)若，且满足，求的大小．
(2)若为锐角三角形．
（ⅰ）证明：．
（ⅱ）若平分，证明：．