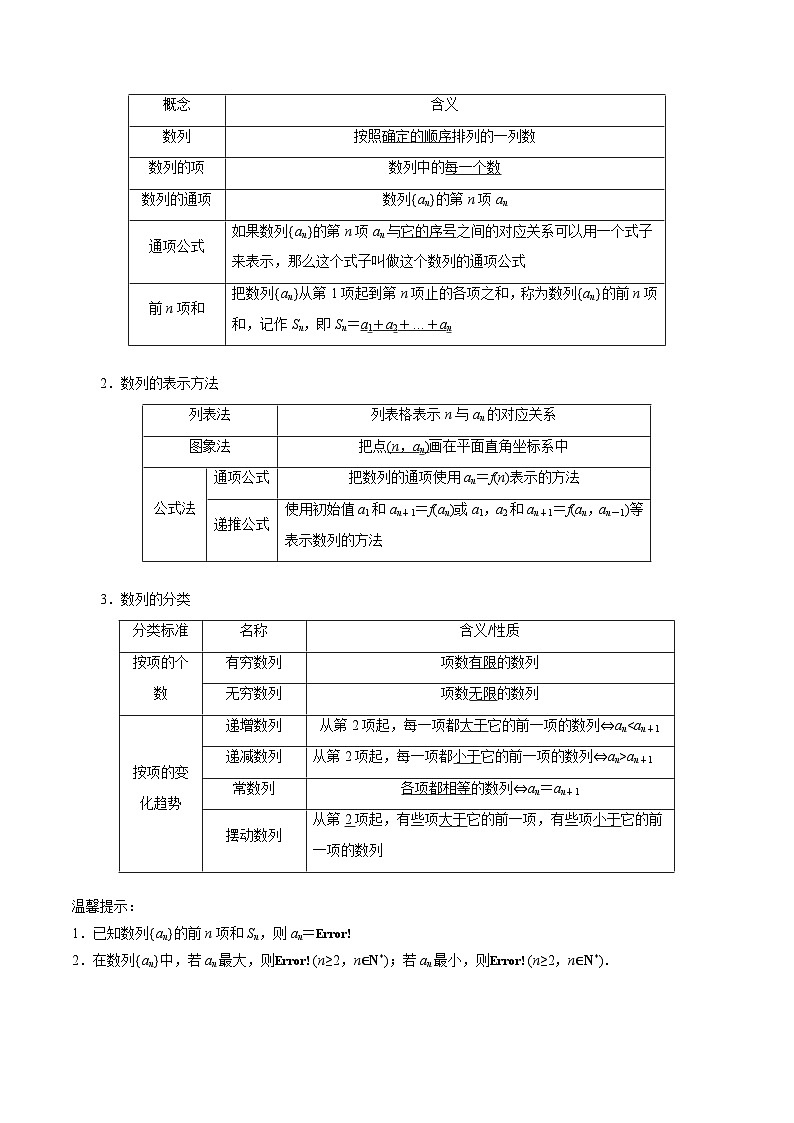
专题22 数列的概念与表示（九大题型+模拟精练+核心素养分析+方法归纳）-2025年高考数学一轮复习 （新高考专用）

这是一份专题22 数列的概念与表示（九大题型+模拟精练+核心素养分析+方法归纳）-2025年高考数学一轮复习 （新高考专用），文件包含专题22数列的概念与表示九大题型+模拟精练原卷版docx、专题22数列的概念与表示九大题型+模拟精练解析版docx、专题22数列的概念与表示思维导图+知识清单+核心素养分析+方法归纳docx等3份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。
2、精练习题。不搞“题海战术”，在老师指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题22 数列的概念与表示（九大题型+模拟精练）
目录：
01 数列的有关概念
02 数列的周期性
03 数列的单调性及应用
04 求数列的通项公式—定义法
05 求数列的通项公式—累加法
06 求数列的通项公式—累乘法
07 求数列的通项公式—an与Sn的关系
08 求数列的通项公式—观察法
09 求数列的通项公式—构造法
01 数列的有关概念
1．（23-24高二上·山西·期末）下列说法中，正确的是（ ）
A．数列可表示为集合
B．数列与数列是相同的数列
C．数列的第项为
D．数列可记为
【答案】C
【分析】利用数列定义即可逐个选项判断即可得解.
【解析】对于A，由数列的定义易知A错误；
对于B，两个数列排列次序不同，是不同的数列，故B错误；
对于C，数列的第项为，故C正确；
对于D，因为，所以，这与数列的定义不相符，故D错误.
故选：C.
2．（2024高三·全国·专题练习）下列三个结论中，正确结论的序号的是（ ）
①数列，，，，，，是无穷数列；
②任何数列都能写出它的通项公式；
③若数列是等差数列，则数列是等比数列.
A．①②B．①③C．②③D．①②③
【答案】B
【分析】根据无穷数列的定义判断①，根据数列的定义判断②，根据等比数列的定义判断③.
【解析】解：数列，，，，，，表示数列有无穷项，所以是无穷数列，故①正确；
不规则数列无法求出其通项，故②错误；
若数列是等差数列，设公差为，所以，整理得，
所以（常数），故数列是等比数列，故③正确.
故选：B
3．（2024高三·全国·专题练习）已知数列满足，若要使为k项的有穷数列，则
A．B．C．D．
【答案】B
【分析】只需时分母有为0即可得解.
【解析】若要使为k项的有穷数列，则时，解得.
故选：B.
【点睛】本题主要考查了数列的通项公式，数列分母不为0是解题的关键，属于基础题.
02 数列的周期性
4．（23-24高二下·辽宁沈阳·阶段练习）在数列中，，，则（ ）
A．B．C．D．2
【答案】A
【分析】根据递推式写出数列前面几项得出数列周期，进一步即可求解.
【解析】由题意可得：，
由此可以发现数列的周期是3，
从而.
故选：A.
5．（23-24高二上·广东湛江·阶段练习）在数列中，，若，则（ ）
A．B．C．D．
【答案】C
【分析】根据递推公式列出数列的前几项，找到规律，即可判断.
【解析】因为且，
所以，，
，，，，
所以是以为周期的周期数列，所以.
故选：C
6．（23-24高二下·四川·期中）已知数列满足，，则数列前2024项的积为（ ）
A．4B．1C． D．
【答案】B
【分析】先找到数列an的周期，然后求得数列an前2024项的积.
【解析】因为，所以，
，所以数列an的周期为4.
由，则，，，
所以数列an前2024项的乘积为.
故选：B.
03 数列的单调性及应用
7．（23-24高二下·青海海西·期中）设数列的通项公式为，若数列是单调递增数列，则实数的取值范围为（ ）
A．B．
C．D．−∞,8
【答案】D
【分析】根据题意有，解得的取值范围；
【解析】由数列是单调递增数列可得，对于都有成立，
即对都成立，
所以．（或通过二次函数的对称性求解）
故选：D.
8．（23-24高二上·江苏南京·阶段练习）已知数列满足：，且数列是递增数列，则实数a的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】由数列的单调性求解．
【解析】由题意，解得.
故选：C.
9．（24-25高三上·山西大同·期末）等比数列中，为其前项和，，且成等差数列，则的最小值为（ ）
A．B．C．D．1
【答案】D
【分析】先根据等差中项及等比数列得通项求出公比，再根据等比数列的前项和公式求出，判断出数列的单调性即可得解.
【解析】设公比为，
由成等差数列，得，
又数列an为等比数列，所以得，解得，
所以，
令，
则，
所以数列递增数列，
所以当时，取得最小值1.
故选：D.
10．（2024·重庆·二模）记正项数列的前项和为，若，则的最小值为 .
【答案】
【分析】由，利用数列通项和前n项和的关系求得，再令，利用导数法求解.
【解析】当时，，则或（舍去），
当时，由，得，
两式相减得，得，
因为，所以，
所以数列是等差数列，则，
令，则，
当时，，当时，，
所以在上单调递减，在上单调递增，
由随的增大而增大，，，
则，
所以的最小值为.
故答案为：.
【点睛】关键点点睛：本题解决的关键是构造函数判断得其单调性，从而考虑，的情况，从而得解.
11．（23-24高二下·辽宁·期末）设数列满足，若对一切，则实数的取值范围是（ ）
A．B．1≤m≤2C．D．
【答案】A
【分析】根据题意列不等式，结合函数的单调性求得的取值范围.
【解析】因为，
设函数，则.
依题意有，注意到在区间上为增函数，
故当时，有最大值，即，解得.
故选：A.
04 求数列的通项公式—定义法
12．（23-24高二下·云南昆明·阶段练习）已知数列满足：，，.
(1)证明：是等差数列，并求的通项公式；
(2)设，若数列是递增数列，求实数的取值范围.
【答案】(1)证明见解析，
(2)
【分析】（1）根据条件，利用等差数列定义，即可证明结果，利用等差数列的通项公式得到，再利用累加法，即可求出结果；
（2）由（1）得，再利用数列bn是递增数列，得到对恒成立，即可求出结果.
【解析】（1）因为，所以为常数，
又，所以数列是公差为，首项为的等差数列.
所以，
当时，，
所以，又，所以，又，满足，
所以数列an的通项公式为.
（2）由（1）知，因为数列bn是递增数列，
所以，对恒成立，
得到对恒成立，所以.
13．（2023·四川成都·模拟预测）数列的前项和为，且.
(1)求的通项公式；
(2)若，的前项和为，求的最小值.
【答案】(1)
(2)
【分析】（1）由可知当时，有，两式作差可求出数列为等比数列，计算即可求出通项公式.（2）裂项相消法求出前项和，根据数列的单调性以及极限的思想即可求出最值.
【解析】（1）因为，所以，即
当时，，则，
整理得（），
则数列是以1为首项，3为公比的等比数列，故，
也满足 所以.
（2）由（1）得
所以
；
显然
又因为，单调递增（），所以，
所以的最小值是.
14．（22-23高三上·天津滨海新·阶段练习）已知是正项数列的前n项和，，，，成等差数列．
(1)求的通项公式；
(2)若，求的前2n项和；
(3)若，证明的前n项和．
【答案】(1)；
(2)；
(3)证明见解析.
【分析】（1）利用，，成等差数列和，即可求出，即可求出奇偶项数列；
（2）分奇偶项分别利用错位相减求和再相加即可求出答案；
（3）利用裂项相消即可得到答案.
【解析】（1）由，，成等差数列得
或（舍）
的奇数项是以首项为1公比为2的等比数列，即
的偶数项是以首项为2公比为2的等比数列，即
则
（2）
（3）
.
05 求数列的通项公式—累加法
15．（2023·广西南宁·模拟预测）数列满足，（为正常数），且，，.
(1)求数列的通项公式；
(2)求数列的前项和.
【答案】(1)
(2)
【分析】（1）由题意可得奇数项成等差数列，设公差为d，且偶数项成等比数列，公比为，运用等差数列和等比数列的通项公式，解方程可得公差d和公比q，即可得到所求通项公式；
（2）讨论n为偶数和奇数，由等差数列和等比数列的求和公式，计算可得所求和.
【解析】（1）数列满足,，
可得成等差数列，即奇数项成等差数列,设公差为,
且偶数项成等比数列,公比为,且，，,
可得,,
解得,
则,化为
（2）当为偶数时,
数列的前项和


当为奇数时,
当时也适合上式.
综上:
16．（23-24高二下·广东深圳·期末）设数列 满足 .
(1)求数列 的通项公式;
(2)求数列 的前 项和 .
【答案】(1)
(2)
【分析】（1）利用累加法求解数列通项公式，再根据分组求和进行化简；
（2）利用裂项相消求解数列的前 项和 ；
【解析】（1）
可知
上式相加得
所以数列 an 的通项公式
（2），
所以
所以数列 的前 项和 .
06 求数列的通项公式—累乘法
17．（23-24高二下·黑龙江大庆·期末）记数列的前项和为，已知且．
(1)求的通项公式；
(2)记，求数列的前项和
【答案】(1)
(2)
【分析】（1）由与的关系式可得数列an的递推公式，利用累乘法可求通项公式；
（2）由（1）知，所以，利用分组求和法求.
【解析】（1）根据题意，，，则，
两式相减得，
即，
所以，
故an的通项公式为；
（2）由（1）知，，所以，
故，
.
18．（23-24高二下·山东日照·期末）已知等差数列的前n项和为，且，.
(1)求数列的通项公式；
(2)设数列的前n项和为，且，令，求的最小值．
【答案】(1)
(2)2
【分析】（1）由等差数列及其前项和基本量的计算即可列方程组求解首项、公差，进而得解；
（2）由（1）中结论结合累乘法得数列的通项公式，通过裂项法得的表达式说明单调递增，或由也可说明单调递增，进而得解.
【解析】（1）设等差数列的首项为，公差为．
由，得，
解得：，所以．
（2）方法一：由（1）得，
由题意，
，
而，从而，
，
而关于单调递减，从而关于单调递增，
所以关于也是单调递增，
所以当时，的最小值为；
方法二：由（1）得，
由题意，
，
而，从而，
又，所以单调递增，
所以的最小值为.
07 求数列的通项公式—an与Sn的关系
19．（23-24高二下·江西萍乡·期中）已知数列的前项和为，且满足．
(1)求的值；
(2)试猜想的通项公式，并证明．
【答案】(1)，
(2)，证明见解析
【分析】（1）由数列的递推式，分别令和，计算可得所求值；
（2）猜想，由数列的递推式和数列的恒等式，可得证明.
【解析】（1）由题知，，解得，
同理，，解得；
（2）由（1）可猜想，证明如下：
已知，当时，有，
化简得，即，
则有，
又，故，
则，
当时，上式仍成立，则．
20．（2024·辽宁·模拟预测）已知数列的前项和为，且．
(1)证明：是等比数列，并求其通项公式；
(2)设，求数列的前100项和．
【答案】(1)证明见解析，．
(2)100.
【分析】（1）利用给定的递推公式，结合及等比数列定义推理得证，再求出通项公式.
（2）利用（1）的结论求出，再利用分组求和法计算即得.
【解析】（1）数列中，，当时，，两式相减得，
而，解得，所以是首项为2，公比为5的等比数列，
通项公式为.
（2）由（1）知，，
所以
．
08 求数列的通项公式—观察法
21．（23-24高二下·四川成都·期中）数列满足，（）．
(1)计算，，猜想数列的通项公式并证明；
(2)求数列的前n项和；
【答案】(1)，，猜测，证明见解析
(2)
【分析】（1）直接通过递推公式计算，然后猜测并证明；
（2）使用错位相减法即可.
【解析】（1），.
猜测，下面用数学归纳法证明：
当时，由知结论成立；
假设结论对成立，即，则，故结论对成立.
综上，有成立.
（2）设数列的前项和为，则.
所以.
故.
22．（2023·山东菏泽·二模）已知各项为正数的等比数列满足.
(1)求数列的通项公式；
(2)设，，求数列的前2n项和.
【答案】(1)；
(2).
【分析】（1）设首项为，公比为q，由可得，化简后可得，即可得答案；
（2）由题可得当为奇数时，，当n为偶数时，.后由分组求和法可得答案.
【解析】（1）设首项为，公比为q.
因，则.
又各项为正数，则，故；
（2）由（1）及题意可得，；
当为奇数时，；
则当为偶数时，.
.
09 求数列的通项公式—构造法
23．（2024·内蒙古包头·三模）已知数列的前n项和为，，．
(1)证明：数列是等比数列，并求；
(2)求数列的前n项和．
【答案】(1)证明见解析，
(2)
【分析】(1)根据题意及，整理可得，即可得证；
(2)根据(1)中可求出分类讨论求出的通项公式，再根据等比数列前n项和可求得.
【解析】（1）因为，又，
所以，整理得．
由题意得，
所以数列是以2为首项，2为公比的等比数列，故，
即．
（2）由（1）可，
当时，，
当时，，
所以，
.
当，代入满足公式，
综上，
24．（23-24高二下·辽宁锦州·期末）已知数列满足，则 .
【答案】
【分析】依题意可得，两边同除得到，即可得到是以为首项，为公差的等差数列，即可求出的通项，即可得解.
【解析】因为，，
则，
因为，显然，
所以，
所以是以为首项，为公差的等差数列，
所以，
所以，则.
故答案为：
25．（23-24高二下·湖南郴州·期末）已知数列满足：．若，则数列的前项和 .
【答案】
【分析】根据给定的递推公式，利用构造法求出，再利用裂项相消法求和即得.
【解析】数列中，由，得，
因此数列是以为首项，1为公差的等差数列，，即，
于是，
所以.
故答案为：
26．（23-24高二下·山东烟台·期末）已知数列是等差数列，且，数列满足，，且.
(1)求数列的通项公式；
(2)将数列的所有公共项按从小到大的顺序组成一个新的数列，求数列的通项公式；
(3)设数列的前项和为，证明：.
【答案】(1)
(2)
(3)证明过程见解析
【分析】（1）首先求得，由累加法即可求解；
（2）不妨设，分，两种情况讨论即可求解；
（3）当时，结论显然成立，当时，通过放缩法以及裂项即可得证.
【解析】（1）由题意可知，即，故，
由，可得，
所以数列的公差，所以，
由，
叠加可得，
整理可得，当时，满足上式，
所以；
（2）不妨设，即，可得，
当时，，不合题意，
当时，，
所以在数列中均存在公共项，
又因为，所以.
（3）当时，，结论成立，
当时，，
所以，
综上所述，.
一、单选题
1．（2024·贵州遵义·二模）已知数列的前项和，则（ ）
A．16B．17C．18D．19
【答案】D
【分析】根据给定条件，利用求出，即可计算即得.
【解析】依题意，，，
所以.
故选：D
2．（2024·全国·模拟预测）在数列中，，，则（ ）
A．8B．1C．18D．19
【答案】D
【分析】利用给定的递推公式，依次计算即得结果.
【解析】因为，，
所以，.
故选：D.
3．（2024·浙江·模拟预测）已知且，则的值为（ ）
A．B．C．D．
【答案】C
【分析】由题意等式两边平方化简为平方得，令，结合二倍角余弦公式得，取，，利用二倍角正弦公式和诱导公式计算的结果；
【解析】平方得，令，
则，
不妨取，则，
故选：C.
4．（2024·西藏·模拟预测）已知数列对任意满足，则（ ）
A．B．C．D．
【答案】A
【分析】由，得，从而，再利用累乘法求解.
【解析】解：由，得，
所以，
所以，即①．
又因为②，
①②两式相乘，得．
故选：A．
5．（2024·天津南开·二模）设数列的通项公式为，若数列是单调递增数列，则实数b的取值范围为（ ）.
A．B．C．D．
【答案】A
【分析】由递增数列定义可得，代入计算即可得解.
【解析】由题意可得恒成立，即，
即，又，，故.
故选：A.
6．（2024·陕西安康·模拟预测）在数列中，，若对，则（ ）
A．B．1C．D．
【答案】A
【分析】根据递推公式得出,进而即可．
【解析】由与相减得：，
即，又，故，所以.
故选：A.
7．（2024·内蒙古赤峰·三模）如图是瑞典数学家科赫在1904年构造的能够描述雪花形状的图案.图形的作法是：从第一个正三角形（边长为1）P1开始，把每条边分成三等份，然后以各边的中间一段为底边分别向外作正三角形，再去掉底边.反复进行这一过程，就得到一条“雪花”状的曲线，称为科赫曲线.设Pn的周长和面积分别为Ln、Sn，下列结论正确的是（ ）
①P₅的边数为
②
③既不是等差数列，也不是等比数列；
④
A．①②③B．①②④C．①③④D．①②③④
【答案】D
【分析】设每个图形的边数为，写出，，，，，可判断①；求得，可判断②；根据等比数列求得，根据迭代累加可得，可判断③④．
【解析】设每个图形的边数为，由题意可得，，，，，…,，故①正确；
，故②正确；
，
第一个图形的面积即正三角形的面积，
从第1个图形到第2个图形，边数增加了，同时每条边上多了一个小三角形，这个小三角形的面积是原图形的，
所以，，
以此类推，第个图形的面积为，
依次迭代，则
，
所以
，故，，故④正确．
，可得既不是等差数列，也不是等比数列，故③正确
故选：D．
8．（2024·辽宁·三模）已知数列中各项均为正数，且，给出下列四个结论：
①对任意的，都有
②数列可能为常数列
③若，则当时，
④若，则数列为递减数列．
其中正确结论有（ ）
A．1B．2C．3D．4
【答案】C
【分析】结合数列递推式研究数列的单调性，逐项判断即可.
【解析】解：对于①，在数列an中，，则，
又对于任意的都有，则，即，
即对于任意的，都有，
所以的值不确定大小，故①项错误；
对于②，不妨设数列an可能为常数列，则，
又，则，则，
即时，数列an为常数列，故②项正确；
对于③，，则，因为数列an中各项均为正数，
即，同理，当，都有，
又，即数列an为递增数列，
即当时，，故③项正确.
对于④，
又，则，即，
同理，当，都有，即，
同理，当，都有，
即，
即，即数列an为递减数列，故④项正确；
故选：C.
【点睛】关键点睛：数列与不等式以及数列与单调性等问题，常利用作差法，需要熟练应用不等式知识解决数列中的相关问题．
二、多选题
9．（2024·山西太原·二模）已知数列满足，，则下列结论正确的是（ ）
A．是递增数列B．是等比数列
C．当n是偶数时，D．，，使得
【答案】BC
【分析】对于A，求出数列的前几项即可判断；对于B，等比数列的定义证明即可；对于C，由B可知，是以为首项，为公比的等比数列，求解判断即可；对于D，由C可知，，结合，所以，分类讨论判断即可.
【解析】对于A：由，，，所以A错误；
对于B：当时，由，，
当时，，
综上所述：所以是以为首项，为公比的等比数列，B正确；
对于C：由B可知，是以为首项，为公比的等比数列，
所以，所以，为偶数，
所以当n是偶数时，，故C正确；
对于D：由C可知，，由，
所以，因为，
所以当时，，
当时，，而，
所以恒成立，故D错误；
故选：BC.
10．（2024·湖南长沙·三模）设无穷数列an的前项和为，且，若存在，使成立，则（ ）
A．
B．
C．不等式的解集为
D．对任意给定的实数，总存在，当时，
【答案】BCD
【分析】根据题意，得到且an是递减数列，结合等差数列的性质以及等差数列的求和公式，逐项判定，即可求解.
【解析】由，可得，
且，即
又由，可得数列an是等差数列，公差，
所以an是递减数列，所以是最大项，且随着的增加，无限减小，即，
所以A错误、D正确；
因为当时，；当时，，
所以的最大值为，所以B正确；
因为，
且，
所以当时，；当时，，所以C正确.
故选：BCD.
11．（2023·浙江·二模）已知递增数列的各项均为正整数，且其前项和为，则（ ）
A．存在公差为1的等差数列，使得
B．存在公比为2的等比数列，使得
C．若，则
D．若，则
【答案】ABC
【分析】运用公式法计算A，B选项，根据数列的性质推导C，D选项.
【解析】对于A，设数列的首项为，则 ，解得 ，
即当等差数列的首项为138，公差为1时， ，正确；
对于B，设首项为 ，则 ，正确；
对于C，欲使得尽可能地大，不妨令 ，则有 ，
又 ，即 ，
，
即 ，正确；
对于D， ， ，即 ，
比如， ，
则 ，D错误；
故选：ABC.
【点睛】思路点睛：数列中与整数有关的不等式或方程问题，注意利用整数的性质来处理.
三、填空题
12．（2024·云南·二模）记数列的前项和为，若，则 .
【答案】/0.5
【分析】构造得，从而得到，则，再利用等比数列求和公式代入计算即可.
【解析】由，得，
则，
又，则，则，
，，
，
故答案为：.
13．（2024·全国·模拟预测）已知数列的前项和为，满足，则 ；数列满足，数列的前项和为，则的最大值为 ．
【答案】
【分析】借助数列与前项和的关系，由得作差即可得；得到后，结合裂项相消法计算即可得，结合数列的函数特性即可得的最大值.
【解析】将代入，得，
当时，由，得，
化简得，
因此数列an是以2为首项，2为公比的等比数列，
故，
，
则，
故，
易知函数在上单调递增，
在上单调递增，
且当时，，
当时，，
所以当时，取得最大值.
故答案为：；.
14．（2024·黑龙江哈尔滨·二模）已知数列中，，且，若存在正整数，使得成立，则实数的取值范围为 .
【答案】
【分析】构造数列先计算，分奇偶讨论结合指数函数的单调性计算即可.
【解析】由，令，
若为奇数，则，
若为偶数，则，
即奇数项与偶数项分别成以为公差的等差数列，
易知，
所以，则，
若为奇数，则
有解，即，
由指数函数的单调性可知；
若为偶数，则
有解，即，
由指数函数的单调性可知；
综上满足题意.
故答案为：
【点睛】易错点睛：首先构造等差数列需要分奇偶项进行讨论，务必注意符号，其次结合指数函数的单调性解不等式有解问题时，注意取值范围的大小，保证有解即可.
四、解答题
15．（2022·重庆·模拟预测）已知数列满足.
(1)求证：是等差数列；
(2)若，求的通项公式.
【答案】(1)证明见解析
(2)
【分析】（1）将原递推关系式变形即可证明；
（2）先求得，再用累加法即可求解.
【解析】（1）由题，即，
是公差为4的等差数列.
（2）
，累加可得
，当时也满足上式
.
16．（2024·辽宁沈阳·模拟预测）已知数列满足，，是数列的前项和，对任意，有
(1)求数列的通项公式；
(2)设，求的前100项的和.
【答案】(1)；
(2)
【分析】（1）根据作差得到，从而得到，结合等差数列的定义计算可得；
（2）由（1）可得，记，则，利用并项求和法计算可得.
【解析】（1）由，，
两式相减得，即，
因为，所以，即，
故是首项为，公差为的等差数列，
所以；
（2）由（1）知，
所以，
记，则，
17．（2024·贵州贵阳·三模）已知正项数列的前项和为，且满足.试求:
(1)数列的通项公式;
(2)记，数列的前项和为，当时，求满足条件的最小整数.
【答案】(1)
(2)9
【分析】（1）由已知结合和与项的递推关系进行转化，结合等差数列的通项公式即可求解；
（2）利用裂项求和求出，然后结合恒成立与最值关系的转化即可求解．
【解析】（1）因为，
当时，，
当时，，
因为，
两式相减得，，
因为，所以，
所以，均为等差数列，，．
所以；
（2）由题意得，，
所以，
因为，
所以，
解得．所以满足条件的最小整数为9．
18．（2024·河北沧州·三模）已知数列满足，，.
(1)求数列的通项公式；
(2)设，数列的前项和为，求证：.
【答案】(1)
(2)证明见解析
【分析】（1）由数列的递推公式，利用累乘法即可求解；
（2）对进行不等式放缩，即可证明不等式.
【解析】（1），，，
，两式相除，得，
当，时，，，即；
当，时，，，即，
综上所述，数列的通项公式为；
（2），
，
又，
.
19．（2024·重庆·模拟预测）进位制是人们为了计数和计算方便而约定的记数方式，通常“满二进一，就是二进制；满八进一，就是八进制；满十进一，就是十进制……；满几进一，就是几进制”．
我们研究的正整数通常是十进制的数，因此，将正整数的各位上的数字分别记为，则表示为关于10的次多项式，即，其中，，记为，简记为．
随着计算机的蓬勃发展，表示整数除了运用十进制外，还常常运用二进制、八进制等等．更一般地，我们可类似给出进制数定义．
进制数的定义：给出一个正整数，可将任意一个正整数，其各位上的数字分别记为，则唯一表示为下列形式：，其中，，并简记为．
进而，给出一个正整数，可将小数表示为下列形式：，其中，，并简记为．
(1)设在三进制数下可以表示为，在十进制数下可以表示为，试分别将转化成十进制数，转化成二进制数；
(2)已知数列an的前项和为，且满足，，数列bn满足，当时，；
①当时，求数列bn的通项公式；
②证明：当时，．
【答案】(1)，
(2)① ②证明见解析
【分析】（1）直接使用进制表示的定义即可；
（2）①利用数学归纳法求得，再用进制表示的定义得到，
②利用通项公式直接证明即可.
【解析】（1）由于，，
故的十进制表示是，的二进制表示是.
（2）①由于，故.
用数学归纳法证明：.
当时，结论显然成立；
假设结论对正整数均成立，考虑的情况.
此时，
所以结论对也成立.
由数学归纳法可知对任意正整数成立.
当时，由已知有
.
所以所求的通项公式为.
②.
【点睛】关键点点睛：本题的关键在于对进制表示定义的理解.