






所属成套资源:沪教版(2020)数学选择性必修第二册同步课件
高中数学沪教版(2020)选择性必修第二册2 导数的几何意义优秀课件ppt
展开
这是一份高中数学沪教版(2020)选择性必修第二册2 导数的几何意义优秀课件ppt,共38页。
导数的几何意义上一小节谈到,研究物体变速运动时,我们把时间分成若干个小时间段,计算每个小时间段中物体的平均速度,借以近似地描述物体的运动状况.当时间段的划分越来越细时,对运动的描述就越来越精确.特别地,在一个时间点周边的时间段越来越小时,如果平均速度趋近于一个稳定值,这个稳定值就是物体运动在这个时间点的瞬时速度. 在几何学中有类似的情境:为了研究一条曲线的特性,我们可以把曲线划分成小段,把连接每一小段两端点的线段看作曲线的这个小片段的近似,当曲线的划分越来越细时,用这些小线段连接起来的折线就越来越接近于原来的曲线.
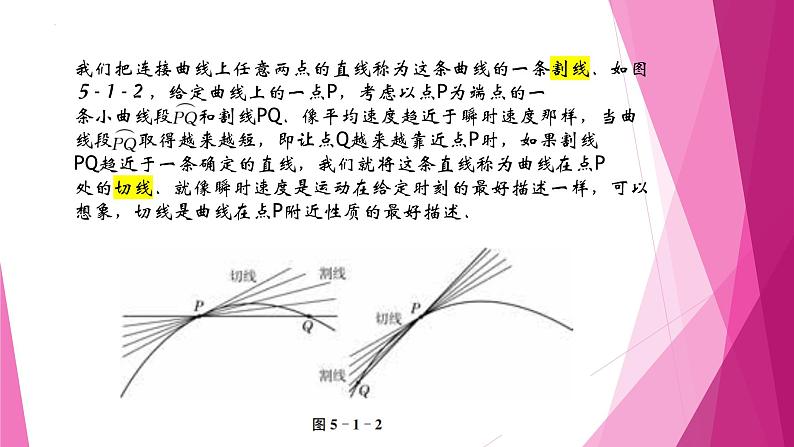
我们把连接曲线上任意两点的直线称为这条曲线的一条割线.如图5-1-2,给定曲线上的一点P,考虑以点P为端点的一条小曲线段 和割线PQ.像平均速度趋近于瞬时速度那样,当曲线段 取得越来越短,即让点Q越来越靠近点P时,如果割线PQ趋近于一条确定的直线,我们就将这条直线称为曲线在点P处的切线.就像瞬时速度是运动在给定时刻的最好描述一样,可以想象,切线是曲线在点P附近性质的最好描述.
切线这个术语并不陌生,我们在平面几何的学习中定义过圆的切线,并讨论过它的性质.那里定义的圆的切线是否与这个新定义一致呢?例3 如图5-1-3,曲线 是圆 在x轴及其上方的部分,点P(1,1)和Q(0, )是该曲线上的点.(1)求割线PQ的斜率;(2)对正整数n,令 在该曲线上取一系列点 借助现代信息技术,适当地计算一些割线 的斜率,观察并总结当n逐渐增大时,割线 的斜率的变化趋势.
解 (1)割线PQ的斜率是 (2)割线 的斜率是借助计算器或计算机可以得到表5-2中关于 的近似计算结果(精确到0.000000001):观察表5 2可知,当n逐渐增大时,割线 的斜率逐渐减小,并趋近于-1.
由例3可以看出,根据现在的定义,曲线在点P(1,1)处的切线的斜率是-1,容易求得它的一般式方程是x+y-2=0.又因为平面几何所定义的切线垂直于过切点的半径,即向量(1,1)是切线的法向量,所以用点法式求出切线的方程也是x+y-2=0.即对于圆来说,两个切线的定义一致. 对于任意曲线y=f(x),如何从定义出发求它在点 P 处的切线?例3给我们的第一个启示是先求切线的斜率.其实,例3还可以进一步揭示斜率的求法:如果记 则
其中 当n增大时, 的稳定值就是这个方法适用于一般情况.如图5-1-4,在曲线上点P 的附近取 一 点 割 线 PQ 的 斜 率 就是函数y=f(x)在以X0和X0+h为端点的区间上的平均变化率。如果当点Q 沿曲线趋近于点P 时,割线PQ的斜率趋近于某一稳定值,那么这个稳定值就是也就是函数y=f(x)在X=X0处的瞬时变化率 因此,函数y=f(x)在X=X0处的导数 )就是曲线y=f(x)在点P处切线的斜率.因此,函数y=f(x)在点P 处的切线方程为
例4 已知 求曲线 在点P(1,1)处的切线方程. 先求曲线y=f(x)在点P(1,1)处切线的斜率f′(1):当h≠0时,从而当h趋近于0时,因此,曲线y=f(x)在点P(1,1)处切线的斜率为2.于是,所求切线方程为即
例5 已知 求曲线y=f(x)在点P(0,0)处的切线方程.解 先求曲线y=f(x)在点P(0,0)处切线的斜率f′(0):当h≠0时,从而当h趋近于0时,因此,曲线 在点P(0,0)处的切线斜率为零,此时曲线的切线是一条水平直线. 通常,我们将导数为零的点称为函数的驻点,曲线在其驻点处的切线是水平直线.
练习5.1(2)1.已知 分别求曲线y=f(x)在点P(-1,3)和点Q(1,3)处的切线方程.2.借助函数图像,判断下列导数的正负(可利用信息技术工具):
习题5.1A组1.自由落体运动的位移S(单位:米)与时间t(单位:秒)满足函数关系 (g为常数).(1)分别求[3,3.1]、[3,3.01]、[3,3.001]时间段内的平均速度;(2)求t=3秒时的瞬时速度;(3)求t=a(a>0)秒时的瞬时速度;(4)借助(3)的结果,求t= 秒时的瞬时速度.2.竖直向上发射的火箭熄火时向上速度达到100米/秒,此后位移S(单位:米)与时间t(单位:秒)近似满足函数关系(1)分别求[0,2]、[2,4]时间段内火箭的平均速度;(2)求t=2秒时火箭的瞬时速度;(3)熄火后多长时间火箭向上速度为0?
3.某水管的流水量y(单位:立方米)与时间x(单位:秒)满足函数关系y=f(x)=3x. (1)求f(x)在x=a处的导数f′(a);(2)f′(a)的实际意义是什么?(3)随着a的取值变化,f′(a)是否发生了变化?为什么?4.石子投入水中,水面产生的圆形波纹区域不断扩散.计算: (1)当半径r从a增加到a+h(h>0)时,圆面积相对于半径的平均变化率;(2)当半径r=a时,圆面积相对于半径的瞬时变化率.5.函数y=f(x)的图像如图所示. (1)求割线PQ的斜率;(2)当点Q沿曲线向点P 运动时,割线PQ的斜率会变大还是变小?
6.已知 求曲线y=f(x)在下列各点处的切线斜率,并说说这些斜率的值是如何变化的.7.借助函数图像,判断下列导数的正负
B组1.已知车轮旋转的角度和时间(单位:秒)的平方成正比,且车辆启动后车轮转动第一圈需要1秒. (1)求车轮转动前2秒的平均角速度;(2)求转动开始后第3秒的瞬时角速度. 2.根据导数的几何意义,求函数 在下列各点处的导数: (1)x=-1; (2)x=0; (3)x=1. 3.已知函数y=f(x)在x=1处的切线方程为y=4x-3,求f(1)和f′(1). 4.如图,直线l是曲线y=f(x)在x=3处的切线,求f′(3)
相关课件
这是一份高中数学沪教版(2020)选择性必修第二册1 导数的概念完美版课件ppt,共19页。PPT课件主要包含了教材分析,新课讲解,课本练习,随堂检测,答案1,答案C等内容,欢迎下载使用。
这是一份高中沪教版(2020)1复平面与复数的坐标表示完整版教学课件ppt,共21页。PPT课件主要包含了学习目标,复习引入,情境导入,新课讲解,复数的几何意义1,课本例题,一一对应,复数的几何意义2,2复数的向量表示,补充例题等内容,欢迎下载使用。
这是一份高中人教A版 (2019)5.1 导数的概念及其意义课文ppt课件,共46页。PPT课件主要包含了自学导引,P0T,瞬时速度,f′x,课堂互动,素养训练等内容,欢迎下载使用。










