数学选择性必修第二册5 利用导数解决实际问题精品ppt课件

这是一份数学选择性必修第二册5 利用导数解决实际问题精品ppt课件，共38页。PPT课件主要包含了答案2等内容，欢迎下载使用。
前面已经看到 ， 导数可用来研究函数在某区间上的最大（ 小 ） 值 ， 从而对解决何时利润最大 、 何时用料最省等优化问题发挥着重要作用
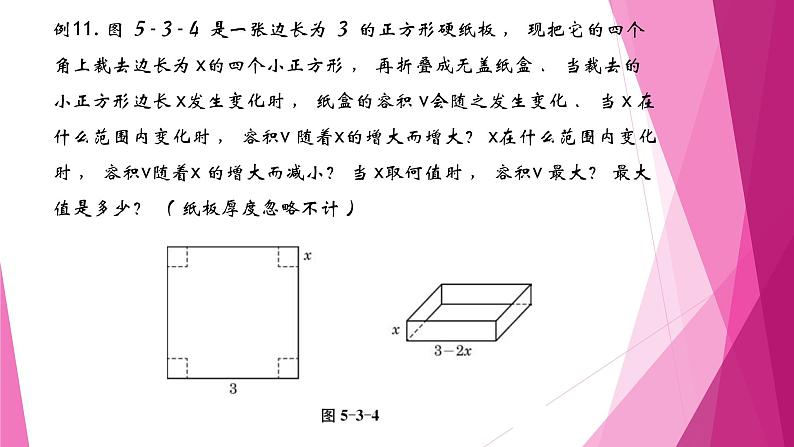
例11. 图 ５-３-４ 是一张边长为 ３ 的正方形硬纸板 ， 现把它的四个角上裁去边长为 x的四个小正方形 ， 再折叠成无盖纸盒 ． 当裁去的小正方形边长 x发生变化时 ， 纸盒的容积 v会随之发生变化 ． 当 x 在什么范围内变化时 ， 容积v 随着x的增大而增大？ x在什么范围内变化时 ， 容积v随着x 的增大而减小？ 当 x取何值时 ， 容积v 最大？ 最大值是多少？ （ 纸板厚度忽略不计 ）
（ １ ） 比较 C ′ （ １０ ） 和 C ′ （ ２０ ）， 解释两者的大小代表了怎样的实际意义 ；（ ２ ） 当产量为多少时 ， 平均成本最少？
在很多情形下 （ 如例 １１ 与例 １３ ）， 由实际问题本身的意义 ，可知函数在区间内部必定存在最大值 （ 或最小值 ）， 而区间内部只有一个驻点 ， 由此即可断定 ： 该函数在区间内部的唯一驻点处取得最大值 （ 或最小值 ）
例14. 一艘船航行所需的燃料费与船速的平方成正比 ． 如果船速是 １０ｋｍ ／ ｈ ， 那么每小时的燃料费是 ８０ 元 ． 已知该船航行的其他费用为每小时 ４８０ 元 ， 在 １００ｋｍ 的航程中 ， 保持怎样的船速可使航行总费用最少？ （ 结果精确到 １ｋｍ ／ ｈ ）
所以 ， 在 １００ｋｍ 的航程中 ， 保持约 ２４ｋｍ ／ ｈ 的船速可使航行总费用最少
２． 采矿 、 采石或取土时 ， 常用炸药包进行爆破 ， 部分爆破呈圆锥漏斗形状 （ 如图 ）， 已知圆锥的母线长是炸药包的爆破半径R ， 它的值是固定的 ． 问 ： 炸药包埋多深可使爆破体积最大？
1、某产品的销售收入y1(万元)是产品x(千台)的函数：y1＝17x2(x>0)；生产总成本y2(万元)也是x的函数：y2＝2x3－x2(x>0)，为使利润最大，应生产(　　)A．9千台 B．8千台 C．6千台 D．3千台【答案】C；【解析】利润函数y＝y1－y2＝18x2－2x3(x>0)，求导得y′＝36x－6x2，令y′＝0，得x＝6或x＝0(舍去).因0