高中沪教版（2020）1正弦函数的图像精品课件ppt

这是一份高中沪教版（2020）1正弦函数的图像精品课件ppt，共38页。PPT课件主要包含了答案A等内容，欢迎下载使用。
前一章学习了三角，无论是在锐角三角形中，还是在平面直角坐标系中，我们都是从几何的角度，把正弦、余弦和正切看成一个比值． 本章我们将从函数的角度看待正弦、余弦和正切，研究这些三角函数的图像与性质． 与幂函数、指数函数及对数函数不同，三角函数具有周期性．在现实生活中存在大量的周期现象，如四季的交替，钟表指针的转动， 弹簧的振动，等等．三角函数是刻画周期现象最典型的数学模型．根据１９世纪法国数学家傅里叶（Ｊ．Ｂ．Ｊ．Ｆｏｕｒｉｅｒ）建立的傅里叶级数理论， 一般的周期函数都可以用正弦函数和余弦函数构成的无穷级数表示，它确认了正弦函数和余弦函数在周期现象研究中重要而本质的作用， 使三角函数成为分析和解决周期问题的基本工具，在物理学、工程技术和其他许多领域都有广泛的应用
我们已经知道，任意一个给定的实数狓都对应着唯一确定的角（其弧度数等于实数x），而这个角又对应着唯一确定的正弦值ｓｉｎx．这样，对于任意一个给定的实数x，都有唯一确定的正弦值ｓｉｎx与之对应．按照这个对应关系所建立的函数叫做正弦函数，记作y＝ｓｉｎx．正弦函数的定义域是实数集R．
对任意给定的实数x，都有ｓｉｎ（x＋２kπ）＝ｓｉｎx，k∈Z． 这说明当x的值增加或减少２π的整数倍时，ｓｉｎx的值会重复出现．因此，只要作出正弦函数y＝ｓｉｎx在区间［０，２π］上的图像， 就可以得到正弦函数在R上的图像． 下面，我们结合单位圆，利用描点法作y＝ｓｉｎx的大致图像．
为了描出y＝ｓｉｎx图像上的某个点M（α，ｓｉｎα），先在平面直角坐标系的x轴上任取一点O１，以点O１为圆心的单位圆与x轴有两个交点，其中右边的一个交点记作A（图７-１-１）．设P是此单位圆上一点，∠AO１P＝α，作PQ垂直于x轴，其垂足为Q．对比以坐标原点O为圆心的单位圆中角α的终边与单位圆的交点，可知点P 的纵坐标为ｓｉｎα，而QP的长是｜ｓｉｎα｜．在x轴上取点N（α，０），将线段QP平移至NM 的位置使点Q与点N重合，从而点 M的坐标为 （α，ｓｉｎα）， 这样就得到了函数y＝ｓｉｎx图像上的一点M．
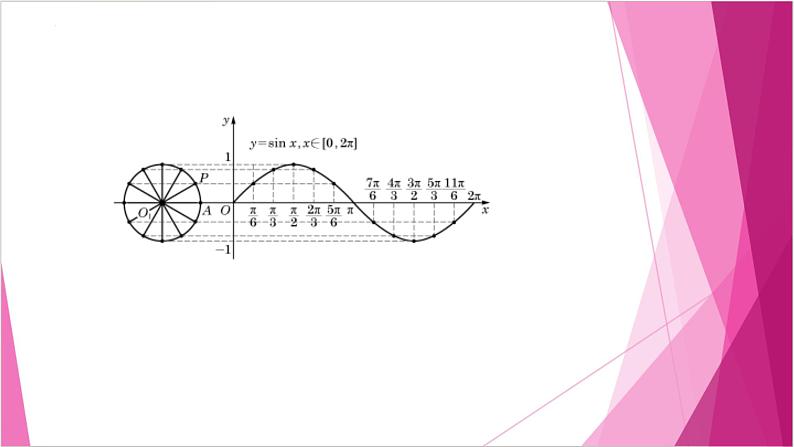
随着α的变化，可以得到函数y＝ｓｉｎx图像上的其他点． 方便起见，我们先将单位圆O１ 分为１２等份（等份数越多，作出的图像越精确），使得角α的弧度数依次取０、 …、２π，再借助圆 O１ 得到对应的纵坐标，依次作出函数y＝ｓｉｎx图像上的点（０，ｓｉｎ０）、 … 、（２π，ｓｉｎ２π），用光滑的曲线将这些点连接起来，就得到正弦函数y＝ｓｉｎx，x∈［０，２π］的大致图像（图７-１-２）
因为ｓｉｎ（x＋２kπ）＝ｓｉｎx，k∈Z，所以函数y＝ｓｉｎx 当 x∈［２π，４π］，x∈［４π，６π］，…时的图像与y＝ｓｉｎx，x∈［０，２π］的图像形状完全一样，只需将后者向右平移２π、４π、…就可得到．同样，函数y＝ｓｉｎx当x∈［－２π，０］，x∈［－４π，－２π］，…时的图像与y＝ｓｉｎx，x∈［０，２π］的图像形状也完全一样，只需将后者向左平移２π、４π、…就可得到．这样，就可以得到函数y＝ｓｉｎx的图像（图７-１-３）．正弦函数y＝ｓｉｎx的图像通常称为正弦曲线
从图７-１-２可知，（０，０）、（π２，１）、（π，０）、（３π２，－１）和 （２π，０）是函数y＝ｓｉｎx，x∈［０，２π］图像的五个关键点．我们描出这五个点，并用光滑的曲线将它们连接起来，就得到函数y＝ ｓｉｎx，x∈［０，２π］的大致图像（图７-１-４）．
这种通过五个关键点作出正弦函数大致图像的方法，通常称为“五点（作图）法”．
例１ 用“五点法”作出函数y＝１－ｓｉｎx，x∈［０，２π］的大致图像，并写出使得y＜１的x的取值范围． 解 将五个关键点列表（表７１）如下：
描点并用光滑曲线把它们连接起来，就得到y＝１－ｓｉｎx， x∈［０，２π］的大致图像（图７-１-５）．
作出函数y＝１的图像，如图７-１-５所示．由图可知，使得y＜１的x的取值范围是 （０，π）．
练习７．１（１） １．作出函数y＝ｓｉｎx，x∈［－π，π］的大致图像． ２．作出函数y＝ －ｓｉｎx，x∈［０，２π］的大致图像，并分别写出使得y＞０和y＜０的 x的取值范围． ３．在同一平面直角坐标系中作出y＝ｓｉｎx和y＝ｓｉｎx＋２的大致图像，并说明它们之间的关系．
1、关于正弦函数y＝sin x的图像，下列说法错误的是（ ）A．关于原点对称 B．有最大值1 C．与y轴有一个交点 D．关于y轴对称
2、函数y＝sin x的图像与函数y＝－sin x的图像关于(　　)A．x轴对称 B．y轴对称 C．原点对称 D．直线y＝x对称
3、用“五点法”作三角函数的图像：在[0，2π]内用“五点法”作出y＝－sinx－1的简图；
【解析】①列表：②描点并用光滑曲线连接可得其图像如图所示．
4、用五点法作出函数y＝1－2sin x，x∈[－π，π]的简图，并回答下列问题：（1）观察函数图像，写出满足下列条件的x的区间：①y>1；②y1；②当x∈(0，π)时，y