湖北省襄阳市老河口市2023-2024学年九年级下学期4月学业水平调研测试数学试卷

这是一份湖北省襄阳市老河口市2023-2024学年九年级下学期4月学业水平调研测试数学试卷，文件包含湖北省襄阳市老河口市2023-2024学年九年级下学期4月学业水平调研测试数学试卷docx、答案docx等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
一、选择题(本大题共10个小题，每小题3分，共30分)
二、填空题(本大题共5个小题，每小题3分，共15分)
11. 1 12. （答案不唯一） 13. 14.25，75 15.
三、解答题(本大题共9个小题，共75分)
16. 解：原式＝－3＋2－＋＋1…………………………………………………………4分
＝．……………………………………………………………………………6分
17.证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，AB＝CD．……………………2分
∵E，F分别为AB，CD的中点，
∴AE＝BE＝BE，DF＝CF＝CD．
∴BE＝DF，BE∥DF．
∴四边形BEDF是平行四边形．…………………………4分
∵AD⊥BD，
∴DE＝BE．………………………………………………5分
∴四边形BEDF是菱形．………………………………6分
18. 解：设原来平均每天生产x个零件，则现在平均每天生产（x＋20）个零件． ……1分
根据题意得，． …………………………………………………………3分
解得，x＝60． ………………………………………………………………………………5分
经检验x＝60是原方程的解．
答：原来平均每天生产60个零件． ……………………………………………………6分
19. 解：(1)6，5． ………………………2分
(2)40－6－12－10－8＝4
补图如图所示． ……………………4分
(3)165． ……………………………………6分
(4) 任选一个意思正确即可． …………8分
从平均数来看，估计该校八年级男生引体向上的平均次数是5.8；从中位数来看，估计该校八年级至少有一半男生引体向上次数不少于6次；从众数来看，估计该校八年级男生引体向上次数5次的人数最多．
20. 解：(1) 因为一次函数y＝x＋1的图象过A (1，a)，B(b，－1)两点，
所以a＝1＋1＝2，……………………………………………………………………………2分
－1＝b＋1，解得b＝－2．…………………………………………………………………4分
因为反比例函数的图象过A，
所以k＝1×2＝2．……………………………………………………………………………6分
(2) m＜－2或0＜m＜1．…………………………………………………………………8分
21. (1) 证明：如图1，连接OC．
∵ OA＝OC，
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
D
C
D
C
C
A
B
B
∴∠OAC＝∠OCA．……………………………………1分
∵AC平分∠DAB，
∴∠OAC＝∠DAC．
∴∠OCA＝∠DAC．
∴AD∥OC．………………………………………………2分
∴∠ADC＋∠OCD＝180°．
∵CD⊥AD，
∴∠OCD＝∠ADC＝90°．
∴OC⊥CD．………………………………………………3分
∵OC是⊙O的半径，
∴CD是⊙O的切线．……………………………………4分
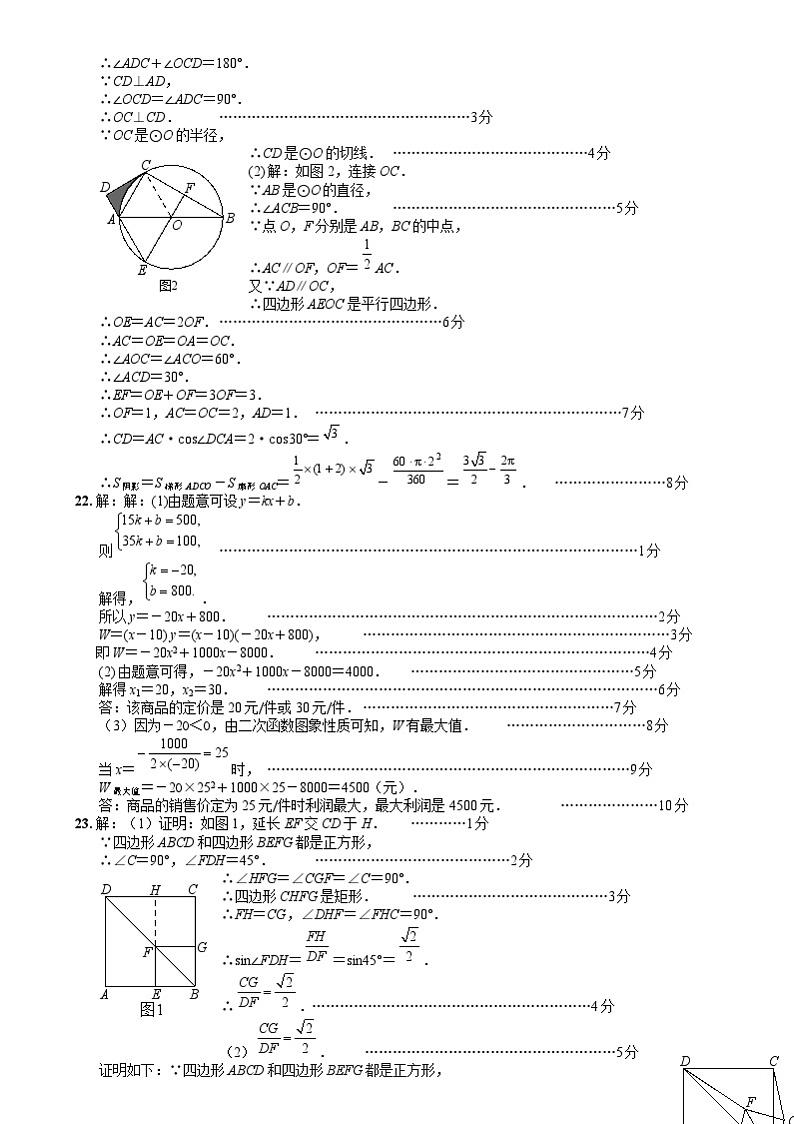
(2) 解：如图2，连接OC．
∵AB是⊙O的直径，
∴∠ACB＝90°．…………………………………………5分
∵点O，F分别是AB，BC的中点，
∴AC∥OF，OF＝AC．
又∵AD∥OC，
∴四边形AEOC是平行四边形．
∴OE＝AC＝2OF．…………………………………………6分
∴AC＝OE＝OA＝OC．
∴∠AOC＝∠ACO＝60°．
∴∠ACD＝30°．
∴EF＝OE＋OF＝3OF＝3．
∴OF＝1，AC＝OC＝2，AD＝1．…………………………………………………………7分
∴CD＝AC·cs∠DCA＝2·cs30°＝．
∴S阴影＝S梯形ADCO －S扇形OAC＝－＝．……………………8分
22. 解：解：(1)由题意可设y＝kx＋b．
则………………………………………………………………………………1分
解得，．
所以y＝－20x＋800．…………………………………………………………………………2分
W＝(x－10) y＝(x－10)(－20x＋800)，…………………………………………………………3分
即W＝－20x2＋1000x－8000．………………………………………………………………4分
(2) 由题意可得，－20x2＋1000x－8000＝4000．…………………………………………5分
解得x1＝20，x2＝30．…………………………………………………………………………6分
答：该商品的定价是20元/件或30元/件．………………………………………………7分
（3）因为－20＜0，由二次函数图象性质可知，W有最大值．…………………………8分
当x＝时，……………………………………………………………………9分
W最大值＝－20×252＋1000×25－8000＝4500（元）．
答：商品的销售价定为25元/件时利润最大，最大利润是4500元． …………………10分
23. 解：（1）证明：如图1，延长EF交CD于H．…………1分
∵四边形ABCD和四边形BEFG都是正方形，
∴∠C＝90°，∠FDH＝45°．……………………………………2分
∴∠HFG＝∠CGF＝∠C＝90°．
∴四边形CHFG是矩形．……………………………………3分
∴FH＝CG，∠DHF＝∠FHC＝90°．
∴sin∠FDH＝＝sin45°＝．
∴．……………………………………………………4分
（2）．………………………………………………5分
证明如下：∵四边形ABCD和四边形BEFG都是正方形，
∴∠DBC＝∠FBG＝45°，∠BCD＝∠BGF＝90°．
∴∠DBC－∠FBC＝∠FBG－∠FBC，即∠DBF＝∠CBG．
，．…………6分
∴．
∴△BDF∽△BCG．………………………………………………6分
∴．……………………………………………… 7分
（3）如图3，连接BD．
∵四边形BEFG是正方形，点F是CG的中点，
∴CF＝FG＝BG＝EF＝BE＝1，∠G＝90°，∠BFG＝∠BFE＝45°．
∴CD＝BC＝．……………………………… 8分
∵∠DBC＝∠FBG，
∴∠DBF＝∠CBG．
由（2）知，
∴△BDF∽△BCG．
∴∠BFD＝∠G＝90°．……………………………………………………………………………9分
∴∠DFC＝180°－∠BFD－∠BFG＝45°，
∠DFE＝∠BFD－∠BFE＝45°．
∴∠DFC＝∠DFE．……………………………………………………………………………10分
又∵EF＝CF，DF＝DF，
∴△DEF≌△DCF，
∴DE＝DC＝．………………………………………………………………………………11分
24．解：(1) b＝－1，c＝4． …………………………………………………………………3分
(2) 如图1，设直线l交x轴于点E，作PF⊥l于点F．
则∠PFD＝∠AED＝∠ADP＝90°．
所以∠DPF＋∠PDF＝∠ADE＋∠PDF＝90°．
所以∠DPF＝∠ADE．
又因为PD＝AD，
所以△ADE≌△DPF．
所以PF＝DE，DF＝AE．
所以EF＝PF＋AE． ………………………………4分
因为，
所以E(－1，0)，AE＝3，PF＝－1－m．
由题意知，P(m，m2－m＋4)，
所以EF＝m2－m＋4．
所以－1－m＋3＝m2－m＋4． ……………………………6分
解得m＝．
m＝2＞－1不合题意，舍去．
所以m＝－2． …………………………………………………7分
(3) ①如图2，过点P作PN∥y轴，交AC于点N．
则△PMN∽△OMC．
∴d＝＝．
当x＝0时，y＝x2－x＋4＝4，所以C(0，4)．
由A，C两点坐标可求得直线AC的解析式为y＝x＋4．
当－4＜m＜0时，PN＝(m2－m＋4)－(m＋4)＝m2－2m，
所以d＝＝m2m． …………………………………………………8分
当OP∥AC时，OP与AC无交点，此时m2－m＋4＝m，解得m＝（负值舍去）．
当0＜m＜2且m≠时，PN＝(m＋4)－(m2－m＋4)＝m2＋2m，
所以d＝＝m2＋m．……………………………………………………9分
②d与m的图象如图3所示，由图象可知0＜d＜．
当－4＜m＜0时，d＝m2m＝(m＋2)2＋．
所以当m＝－2时，d的最大值是． ………………………………………………………10分
由图象可知：
（ⅰ）当0＜d＜时，对d的每个取值，点P有3个；
（ⅱ）当d＝时，符合条件的点P有2个；
（ⅲ）当＜d＜且d≠1时，对d的每个取值，点P有1个． ………………………12分