四川省广安友谊中学2024-2025学年九年级上学期期中检测数学试题

这是一份四川省广安友谊中学2024-2025学年九年级上学期期中检测数学试题，文件包含四川省广安友谊中学2024-2025学年九年级上学期期中检测数学试题docx、初三数学答题卡pdf等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。

数 学
（考试时间：120分钟 满分：120分）
注意事项：
1.本试卷分试题卷（1~6页）和答题卡两部分。
2.试题卷第Ⅰ部分每小题选出答案后，请用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，请用橡皮擦干净后，再改涂其它答案标号。试题卷第Ⅱ部分答在答题卡上。答卷前，考生务必将自己的姓名、班级、准考证号、涂写在答题卡上。
3.考试结束后，只交答题卡。
一、选择题（本大题共10小题，每小题3分，共30分）
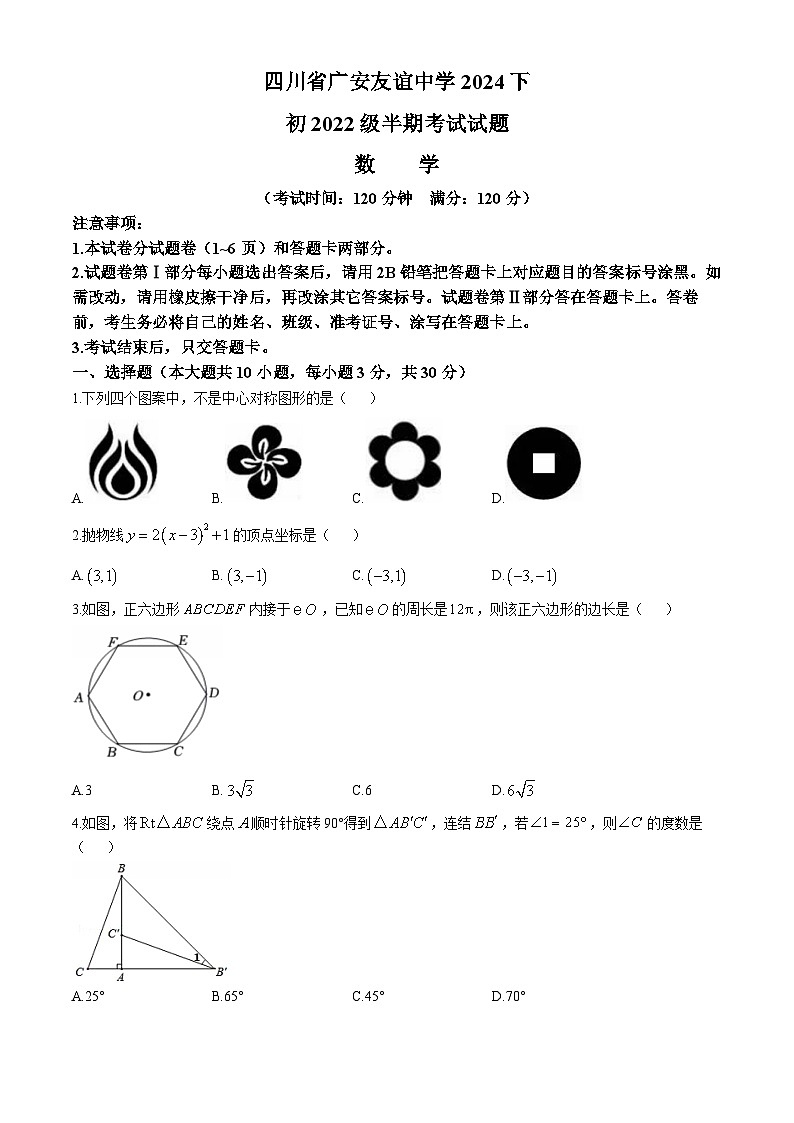
1.下列四个图案中，不是中心对称图形的是（ ）
A.B.C.D.
2.抛物线的顶点坐标是（ ）
A.B.C.D.
3.如图，正六边形内接于，已知的周长是，则该正六边形的边长是（ ）
A.3B.C.6D.
4.如图，将绕点顺时针旋转90°得到，连结，若，则的度数是（ ）
A.25°B.65°C.45°D.70°
5.如图，直线、切于、两点，在上，如果，则等于（ ）
A.40°B.50°C.65°D.130°
6.已知的半径为6，点到圆心的距离为4，则点在（ ）
A.内B.上C.外D.无法确定
7.已知二次函数的图像与轴的一个交点为，则关于的一元二次方程的两个实数根是（ ）
A.，B.，C.，D.，
8.下列说法中，正确的是（ ）
A.在同圆或等圆中，相等的弦所对的圆周角相等
B.平分弦的直径垂直于弦
C.三角形的外心是三条高的交点
D.三角形的内心到三边的距离相等
9.一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开扇形的圆心角是（ ）
A.90°B.120°C.150°D.180°
10.如图，抛物线与轴交于点和，与轴交于点.下列结论：①；②；③；④.其中正确的结论有（ ）个
A.1B.2C.3D.4
二、填空题（本大题共8小题，每小题3分，共24分）
11.某种水果的原价为15元/箱，经过连续两次涨价后售价为30元/箱.设平均每次增长的百分率为，根据题意，列方程为______________________.
12.将抛物线的图像向右平移3个单位长度，再向上平移4个单位长度，得到的抛物线解析式为______________________；若，，为平移后函数图像上的点，则，，的大小关系是______________________（用“<”连接）；
13.数学兴趣小组对如图所示的二维码开展数学实验，已知二维码区域的大正方形边长为2，通过计算机随机掷点的大量重复实验，发现掷点落在黑色区域的频率稳定在0.75左右，由此可以估计白色部分的面积约为______.
14.如图，半圆的直径，弦，，则图中阴影部分的面积为________.
15.一名男生在体育考试时投掷实心球，已知实心球行进高度与水平距离之间的函数关系式是如图，则这名男生掷出实心球的水平距离是________________m.
16.关于的一元二次方程有两个不相等的实数根，则的取值范围是________.
17.如图，已知点，的半径为1，，，点是上的动点，点是的中点，则的最小值是________.
18.如图所示的中，，，，点、在直线上，将绕着点顺时针旋转到位置①得到直线上的点，将位置①的三角形绕点顺时针旋转到位置②得到直线上的点，……按此规律旋转至点，则________________.
三、解答题（本大题共8小题，共66分，解答应写出文字说明，证明过程或演算步骤）
19.解下列方程（共6分）
（1）（2）
20.按要求解决实际问题（共6分）
（1）有一个横断面为抛物线形的拱桥，建立如图所示的平面直角坐标系，当水面宽时，拱桥顶距离水面2m，当水面下降1m时，水面宽度是多少米？
（2）如图是平放在地上的油漆桶横截面，已知油漆桶直径为26cm，油漆面宽度为24cm，求油漆的最大深度是多少？
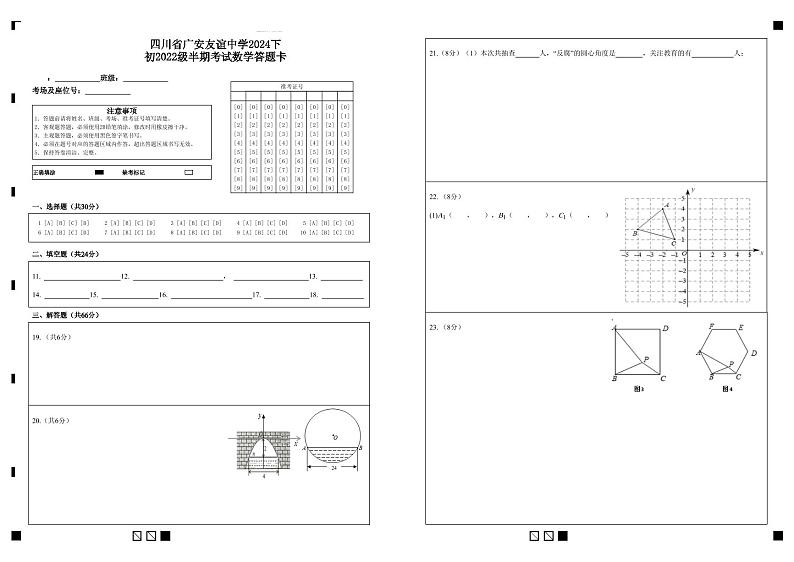
21.（8分）某网站调查；2024年网民们关注的热点话题为：消费、教育、环保、反腐及其它共五类.根据抽样调查的相关数据绘制统计图表如下，根据信息解答下列问题：
（1）本次共抽查______人，“反腐”的圆心角度______，关注教育的有______人；
（2）某市约有2800万人，由上述数据估计该市关注“消费”的人数是多少？
（3）某部门有甲、乙、丙、丁四人关注教育问题，现准备从这四人中随机抽取两人进行座谈，请用列表法或树状图法计算抽取的两人恰好是甲和乙的概率；
22.（8分）如图，已知顶点的坐标分别为，，，按要求完成下列问题（作图时必须标注出顶点字母）；
（1）画出绕点旋转180°的，写出顶点坐标（ ， ），（ ， ），（ ， ）；
（2）画出绕点顺时针旋转90°的；
（3）在（2）的旋转过程中，求点旋转到点经过的路径长（结果保留）；
23.（8分）阅读下列材料：
【提出问题】如图1，在等边三角形内有一点且，，.求的度数；
【解决问题】如图2，将..绕点逆时针旋转60°得到，连接，可得等边，则，且，又由可得且，所以；
【类比问题】（1）如图3，在正方形内有一点且，，.求的度数；
【探索问题】（2）如图4，在正六边形内有一点且，，，则______；
24.（10分）“好又来快餐店”试销一种成本5元的盒饭后发现：若售价不超过10元，每天可售这种盒饭400盒；若售价超过10元，则售价每提高1元，这种盒饭的销量会减少40盒；已知店里每天的固定支出为600元，设每盒盒饭的售价为元，每天的纯收入为元（每天纯收入=每天销售额-每天盒饭成本-每天固定支出）；
（1）试写出与的函数关系式；
（2）这种盒饭售价定为多少时每天纯收入最大？最大为多少？
25.（10分）如图，内接于，是直径，切线切于，交的延长线于点，交于点，交于点；
（1）写出与的关系：__________________；
（2）求证：是的切线；
（3）若，，求阴影部分的面积.
26.（10分）如图1，抛物线经过点、，，顶点为；
（1）求该抛物线的解析式及顶点的坐标；
（2）如图2，若点在抛物线上，点是直线上方抛物线上一动点，连接，，当的面积最大时，求点的坐标及面积的最大值；
（3）如图3，经过点、两点的直线与轴交于点，在抛物线上是否存在一点，使以、、、为顶点的四边形是平行四边形？若存在，请直接写出点的坐标；若不存在，请说明理由.
四川省广安友谊中学2024下
初2022级半期考试数学参考答案
选择题：1~10 AACDC ABDBC
填空题：11. 12. 13.1
14. 15.10 16.且 17.2 18.8097
解答题：19.（1）， （2）
20.（1） （2）8
21.（1）1400，72°，350（2）840万（3）（抽取甲和乙）
22.（1）（2）如图，，（3）
23.（1）135°（2）120°
24.（1）
（2）①时，②时，
则售价12.5元时每天收入最大为1650元.
25.（1）垂直平分（2）略（3）
26.（1），（2），（3）