高中数学沪教版（2020）必修第二册2余弦定理精品课件ppt

这是一份高中数学沪教版（2020）必修第二册2余弦定理精品课件ppt，共46页。PPT课件主要包含了学习目标，数学学科素养，千岛湖等内容，欢迎下载使用。

1．掌握余弦定理的表示形式及证明余弦定理的向量方法，并会运用余弦定理解决两类基本的解三角形问题；2．培养学生在方程思想指导下处理解三角形问题的运算能力；通过三角函数、余弦定理、向量的数量积等知识间的关系，来理解事物之间的普遍联系与辩证统一.
1.数学抽象：余弦定理及其推论；2.逻辑推理：余弦定理在边角互化中的应用；3.数学运算：解三角形；4.数学建模：通过将三角函数、余弦定理、向量的数量积等知识间联系起来，体现了知识之间的辩证统一.
1、正弦定理：2、正弦定理的变型：3、正弦定理的应用：（1）已知三角形两角和任意一边 （2）已知三角形两边和其中一边的对角（注意解得个数）
练习：在△ABC中，由下列条件判断三角形解的个数
(1) A＝30，a＝10，b＝20；(2) A＝30，a＝10，b＝8；(3) A＝30，a＝10，b＝15；(4) A＝120，a＝10，b＝5；(5) A＝120，a＝10，b＝15.
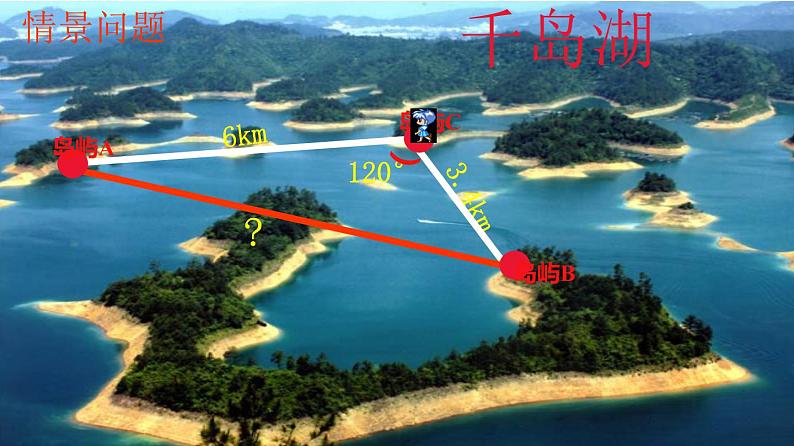
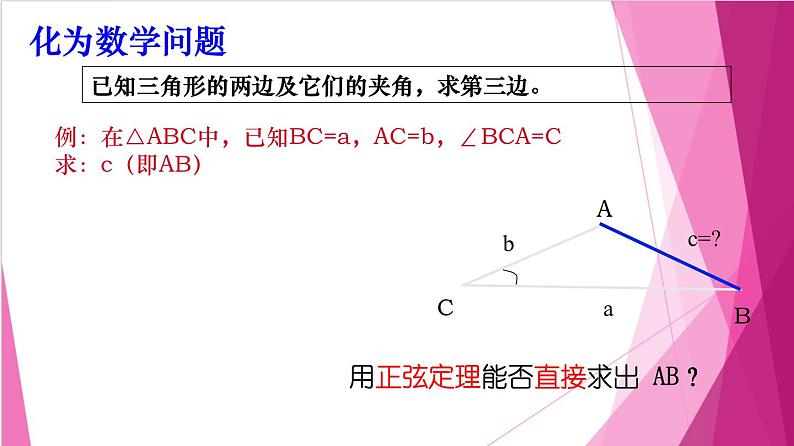
已知三角形的两边及它们的夹角，求第三边。
例：在△ABC中，已知BC=a，AC=b，∠BCA=C求：c（即AB）
用正弦定理能否直接求出 AB？
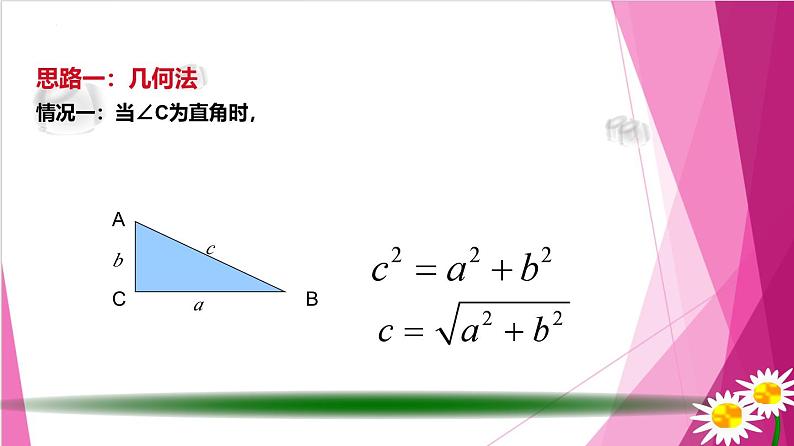
思路一：几何法情况一：当∠C为直角时，
情况二：当∠C为锐角时，
综上，我们得到：在△ABC中，已知a、b，和角C，则
(bcsC,bsinC)
解:以C为原点,BC为x轴建立直角坐标系
例1：在⊿ABC中，已知b=60cm,c=34cm,A=41°,解三角形（角度精确到1°，边长精确到1cm）.
解：根据余弦定理，a²=b²+c²－2bccsA=60²+34²－2×60×34× cs41°≈1676.82所以 a≈41(cm)
因为c不是三角形中最大的边，所以C是锐角，利用计算器得C≈33°
应用题型一、已知三角形的两边及夹角（或其中一边的对角）求解三角形
例2.在△ABC中，已知a= ,b=2 , c= , 解三角形(依次求解A、B、C).
题型二、已知三角形的三边解三角形
在解三角形的过程中，求某一个角有时既可以用余弦定理，也可以用正弦定理，两种方法有什么利弊呢？
　　　　　　在解三角形的过程中，求某一个角有时既可以用余弦定理，也可以用正弦定理，两种方法有什么利弊呢？
在已知三边和一个角的情况下：求另一个角
㈠用余弦定理推论，解唯一,可以免去判断舍取。
㈡用正弦定理，计算相对简单，但解不唯一，要进行判断舍取
例3、在△ABC中,若a=4、b=5、c=6（1)试判断角C是什么角？（2）判断△ABC的形状
题型三、判断三角形的形状
在△ABC中，若　　　　　　 ，则△ABC的形状 为（　）
Ａ、钝角三角形　　　　　　Ｂ、直角三角形Ｃ、锐角三角形　　　　　　Ｄ、不能确定
锐角三角形ABC中，三边长为1,2，x.求x范围
例4 在△ABC中，a，b，c分别是A，B，C的对边，且 2asinA＝(2b＋c)sinB＋(2c＋b)sinC.(1)求A的大小；(2)若sinB＋sinC＝1，试判断△ABC的形状．
题型分析 举一反三
解题技巧(已知三边解三角形的解题思路)
解题技巧(已知两边及一角解三角形的方法及注意事项)
解题技巧(余弦定理在边角转化中的作用)
余弦定理可以解决的有关三角形的问题：1、已知两边及其夹角，求第三边和其他两个角。2、已知三边求三个角；3、判断三角形的形状
数学思想：化归思想、数形结合的思想、 分类讨论的思想