高中7.1 正弦函数的图像与性质一等奖ppt课件

这是一份高中7.1 正弦函数的图像与性质一等奖ppt课件，共60页。PPT课件主要包含了正弦函数的图像探究，正弦函数，正弦函数的性质，题型示例，描点作图，2列表，解析列表等内容，欢迎下载使用。
结合单位圆利用描点法做y=sinx的图像
y=sinx x[0,2]
y=sinx xR
sin(x+2k)=sinx, kZ

连线：用光滑曲线 将这些点连结起来
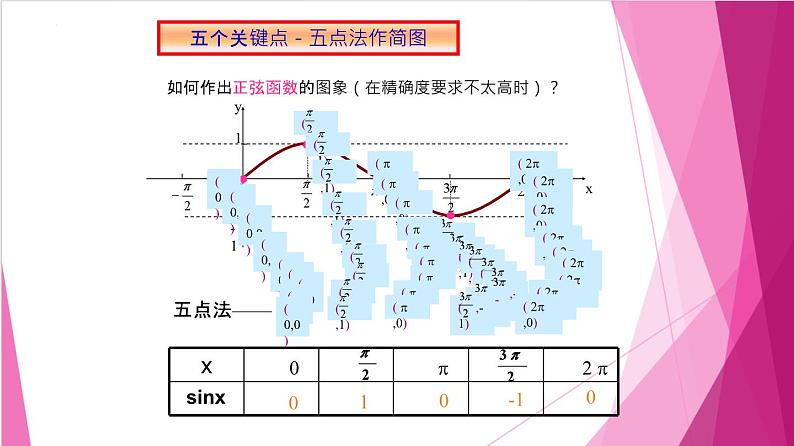
1.正弦函数的图像(1)“五点法”画图:在精确度要求不太高时,我们可以找出正弦曲线上的(0,0),________, _______,__________,(2π,0)五个关键点画出正弦函数在一个周期上的图像.
(2)正弦曲线:将函数y=sin x(x∈[0,2π])的图像向左、向右平行移动(每次平移____个单位长度),就可以得到正弦函数y=sin x(x∈R)的图像._________的图像叫作正弦曲线.
【思考】利用五点法作函数y=Asin x(A>0)的图像时,选取的五个关键点是什么?提示:依次是(0,0), ,(π,0), ,(2π,0).
如何作出正弦函数的图象（在精确度要求不太高时）？
五个关键点－五点法作简图
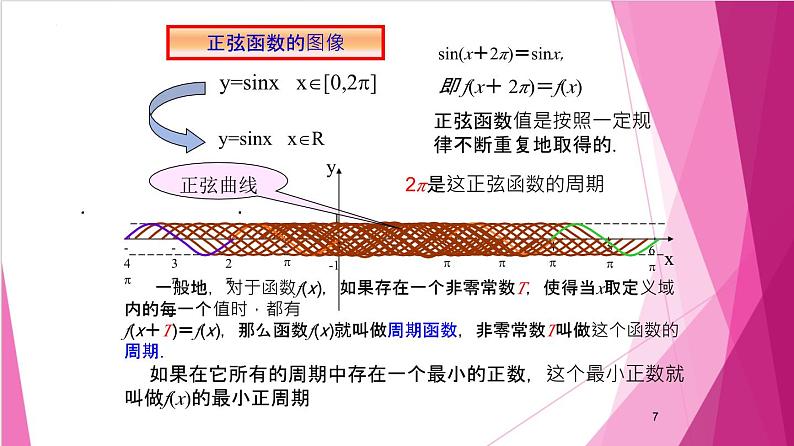
sin(x＋2π)＝sinx，
即 f(x＋ 2π)＝f(x)
正弦函数值是按照一定规律不断重复地取得的.
2π是这正弦函数的周期
一般地，对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.
如果在它所有的周期中存在一个最小的正数，这个最小正数就叫做f(x)的最小正周期
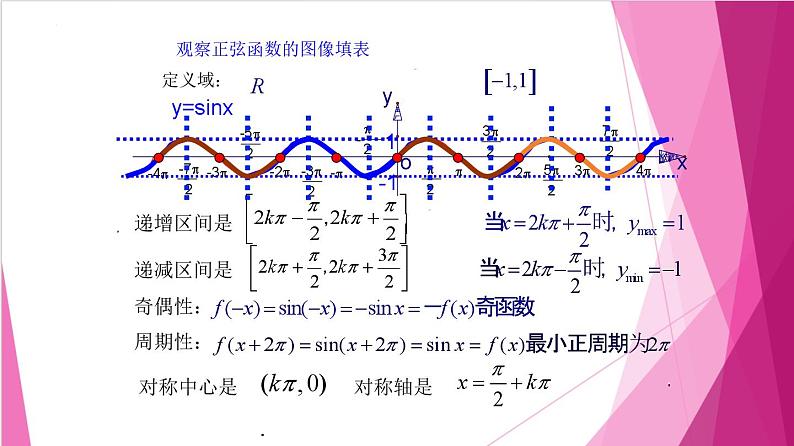
观察正弦函数的图像填表
【思考】如何求正弦函数的递增区间?提示:求一个完整的递增区间,例如, ,再在区间两个端点上加周期的整数倍,即 ,k∈Z.
【基础小测】1.辨析记忆(对的打“√”,错的打“×”)(1)用“五点法”画图时的“五点”是正弦函数图像的一个最高点,一个最低点,三个和x轴的交点.(　　)(2)函数y=sin x的图像关于原点对称.(　　)(3)正弦函数y=sin x是周期函数.(　　)(4)正弦函数y=sin x的最大值为1,最小值为-1.(　　)
提示:(1)√.由“五点法”作图的五点坐标可知(1)是正确的.(2)√.函数y=sin x为奇函数,其图像关于原点对称.(3)√.正弦函数y=sin x是周期为2π的周期函数.(4)√.根据正弦函数的性质可知.
2.点M 在函数y=sin x的图像上,则m的值为(　　)【解析】选B.将 代入y=sin x中,得m=
求下列三角函数的周期：
因为sin(2+z)=sinz
即 f (x+2)=f (x)
则3sin(z+2)=3sinz
即 f (x+4)=f (x)
∴周期T=4
(1)y＝sin2x（x∈R）的周期为2π/2=π;
的周期为2π/(1/2)=4π.
函数 在什么区间上是增函数?
∴ 函数 在区间
类型一　“五点法”作函数的图像(直观想象)【题组训练】 1.利用“五点法”作出y=-2+sin x(x∈[0,2π])的简图.2.作出函数y=-2sin x(0≤x≤2π)的简图.
　【解析】1.按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示)
2.按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示).
【解题策略】“五点法”作图中“五点”的含义
【拓展延伸】正弦曲线的简单变换(1)函数y=-sin x的图像与y=sin x的图像关于x轴对称.(2)函数y=sin x与y=sin x+k的图像间的关系.当k>0时,把y=sin x的图像向上平移k个单位得到函数y=sin x+k的图像;当k