九年级数学第三次月考卷（测试范围：人教版五四制九上~九下33.2）2024+2025学年初中上学期第三次月考

这是一份九年级数学第三次月考卷（测试范围：人教版五四制九上~九下33.2）2024+2025学年初中上学期第三次月考，文件包含九年级数学第三次月考卷全解全析人教版五四制docx、九年级数学第三次月考卷考试版A4测试范围人教版五四制九上九下332docx、九年级数学第三次月考卷参考答案人教版五四制docx、九年级数学第三次月考卷考试版A3测试范围人教版五四制九上九下332docx、九年级数学第三次月考卷答题卡人教版五四制docx、九年级数学第三次月考卷答题卡人教版五四制pdf等6份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
（满分120分，时间120分钟）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
4．测试范围：人教版五四制九年级第二十八章到第三十三章33.2，分布大概如下：第二十八章（19%）、第二十九章（15%）、第三十章（10%）、第三十一章（27%）、第三十二章（10%）、第三十三章（19%）。
5．难度系数：0.65。
第Ⅰ卷（选择题 共30分）
一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知点在反比例函数的图象上，则的值为（ ）
A．2B．C．D．
【答案】B
【解析】解：∵点在反比例函数的图象上，
∴，
故选：B．
2．在平面直角坐标系中，点关于原点对称的点的坐标为（ ）
A．B．C．D．
【答案】D
【解析】解：在平面直角坐标系中，点关于原点对称的点的坐标为．
故选：D．
3．把抛物线向下平移1个单位长度，再向左平移1个单位长度，得到的抛物线解析式为（ ）
A．B．
C．D．
【答案】B
【解析】解：把抛物线向下平移1个单位长度，再向左平移1个单位长度，得到的抛物线解析式为．
故选：B．
4．如图，圆锥的底面半径为，高为，则圆锥的侧面积为（ ）
A．B．C．D．
【答案】C
【解析】解：由勾股定理得，圆锥的母线长为，
∵圆锥的底面周长为，
∴圆锥的侧面展开扇形的弧长为，
∴圆锥的侧面积为：．
故选：C．
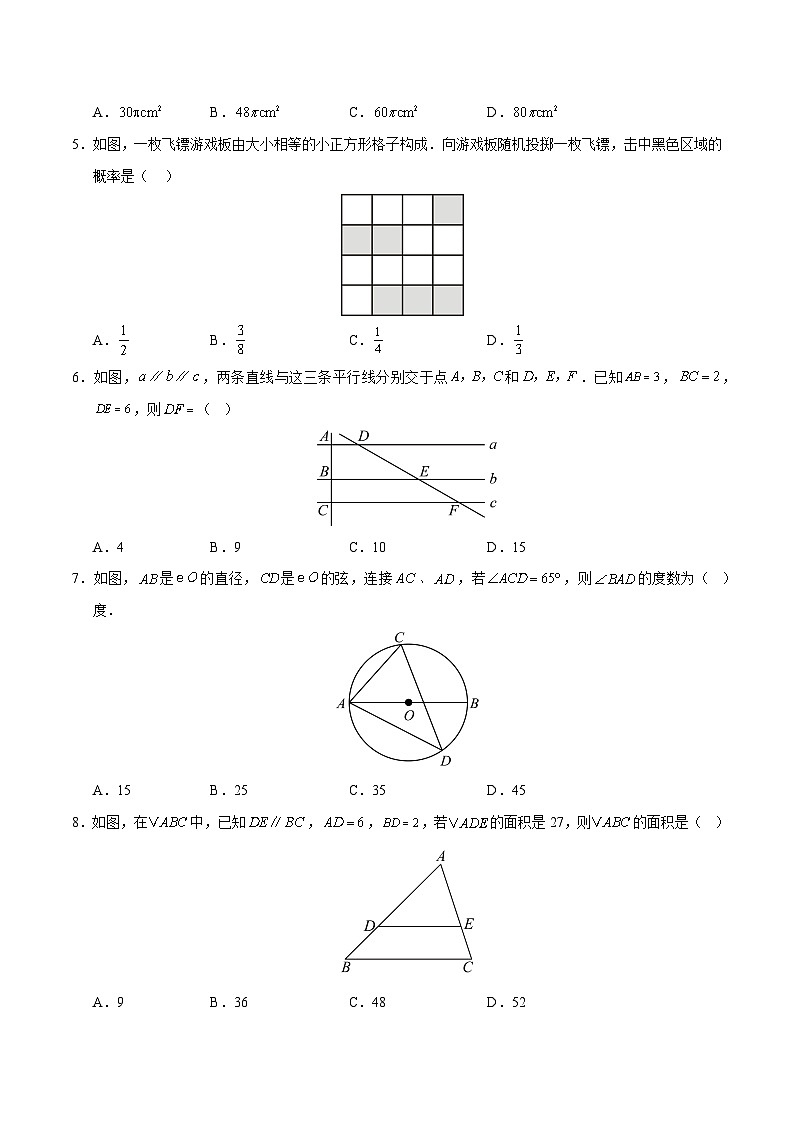
5．如图，一枚飞镖游戏板由大小相等的小正方形格子构成．向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（ ）

A．B．C．D．
【答案】B
【解析】解：随意投掷一个飞镖，击中黑色区域的概率是=，
故选B
6．如图，，两条直线与这三条平行线分别交于点和．已知，，，则（ ）
A．4B．9C．10D．15
【答案】C
【解析】解：已知，，
∴，
∵，
∴，即，
∴，
故选：C ．
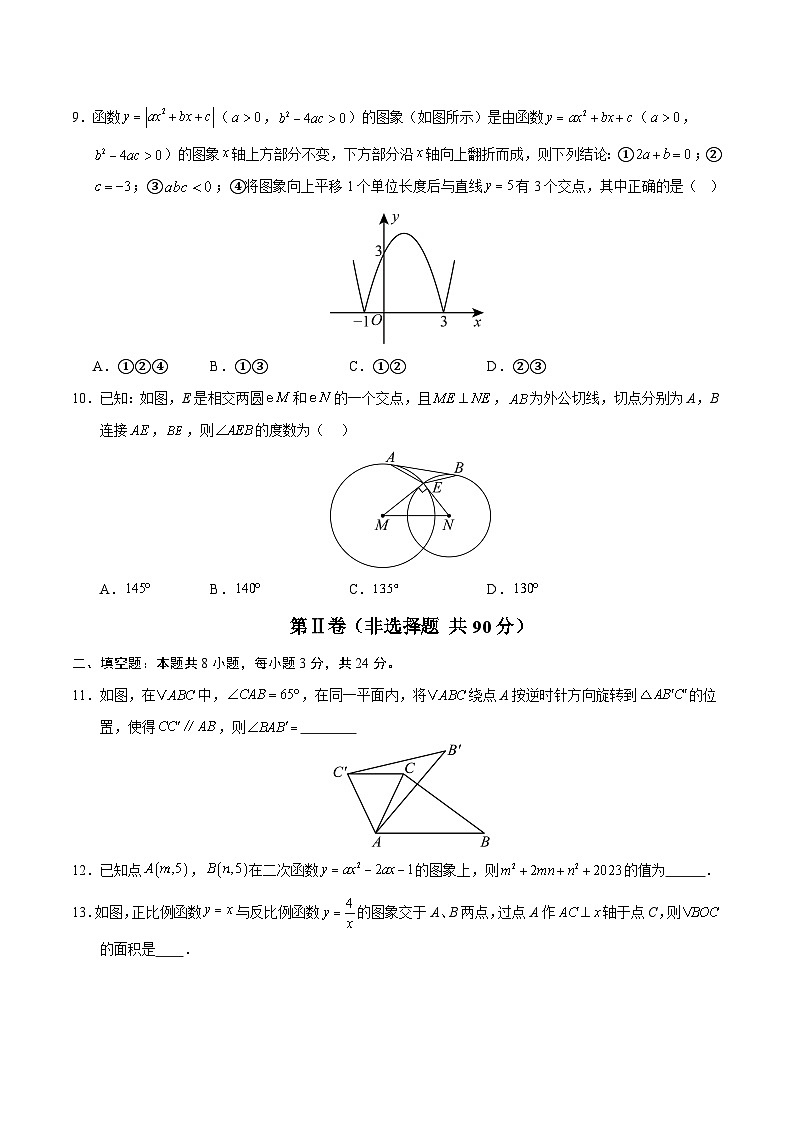
7．如图，是的直径，是的弦，连接、，若，则的度数为（ ）度．
A．15B．25C．35D．45
【答案】B
【解析】解：连接，
∵是直径，∴，
∴，
∵，∴，
∴，
故选：B．
8．如图，在中，已知，，，若的面积是27，则的面积是（ ）
A．9B．36C．48D．52
【答案】C
【解析】解：∵，∴，，
∴，∴，
，，
，
，
，
，
∴的面积是48，
故选：C．
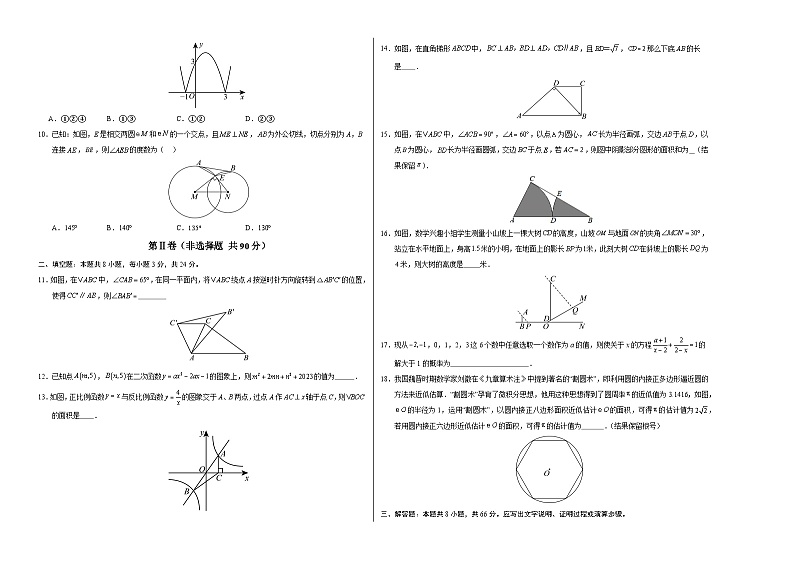
9．函数（，）的图象（如图所示）是由函数（，）的图象轴上方部分不变，下方部分沿轴向上翻折而成，则下列结论：①；②；③；④将图象向上平移1个单位长度后与直线有3个交点，其中正确的是（ ）
A．①②④B．①③C．①②D．②③
【答案】A
【解析】解：由图知，函数（，）的图象与轴交于，，
函数对称轴为直线，，则，，故①正确；
函数图象与轴交于（0,3），由翻折性质可知，，故②正确；
，对称轴为直线，，
，，故③错误；
由图知，，
函数图象与轴交于（0,3），
过点，即，解得，
函数为，
即，
当时，，
即的顶点坐标为（1,4），
将图象向上平移1个单位长度后的顶点坐标为，
将图象向上平移1个单位长度后与直线有3个交点，故④正确．
综上所述，正确的有①②④，
故选：A．
10．已知：如图，E是相交两圆和的一个交点，且，为外公切线，切点分别为A，B连接，，则的度数为（ ）
A．B．C．D．
【答案】C
【解析】解：连接，，延长与交于点H，连接，
∴，∴，
∵为外公切线，∴，，
∴，，∴，∴，
∵，∴，∴，
∴，同理可得：，
∴，
∵，∴．
∵，∴，
∴，
∴，
∴．故选：C．
第Ⅱ卷（非选择题 共90分）
二、填空题：本题共8小题，每小题3分，共24分。
11．如图，在中，，在同一平面内，将绕点A按逆时针方向旋转到的位置，使得，则
【答案】
【解析】解：∵，∴．
∵由旋转的性质可知：，
∴，，
∴，∴．故答案为：．
12．已知点，在二次函数的图象上，则的值为 ．
【答案】2027
【解析】解：二次函数的图象的对称轴是直线，
∵点A，B的纵坐标相等且都在二次函数的图象上，
∴点A，B关于二次函数图象的对称轴对称，
∴=1，∴，
∴．
故答案为：2027．
13．如图，正比例函数与反比例函数的图象交于A、B两点，过点A作轴于点C，则的面积是 ．
【答案】2
【解析】解：联立，解得或，
∴的坐标是，的坐标是，
过作轴于，则，
∵轴，
∴
则的面积是．
故答案为：2．
14．如图，在直角梯形中，，且，那么下底的长是 ．
【答案】
【解析】解：∵，
∴，，
∴，∴．
∵，
∴．
故答案为：．
15．如图，在中，，，以点为圆心，长为半径画弧，交边于点，以点为圆心，长为半径画圆弧，交边于点，若，则图中阴影部分图形的面积和为 （结果保留）．
【答案】
【解析】解：在，，，，
，，
阴影部分的面积，
故答案为：．
16．如图，数学兴趣小组学生测量小山坡上一棵大树的高度，山坡与地面的夹角，站立在水平地面上，身高米的小明，在地面上的影长为米，此刻大树在斜坡上的影长为米，则大树的高度是 米．
【答案】
【解析】解：过点作于点，如图，
，，
米，米，
米，
由题意得：米，米，，
，即，米，
米，大树的高度是米，
故答案为：．
17．现从，0，1，2，3这6个数中任意选取一个数作为a的值，则使关于x的方程的解大于1的概率为 ．
【答案】
【解析】解：解方程得：，
∵其解大于1，∴，，
∴a>0，且，
∴-2，，0，1，2，3这6个数中，符合条件的值为：2，3，
∴取到满足条件的值的概率为，故答案为．
18．我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率的近似值为3.1416，如图，的半径为1，运用“割圆术”，以圆内接正八边形面积近似估计的面积，可得的估计值为，若用圆内接正六边形近似估计的面积，可得的估计值为 ．（结果保留根号）

【答案】
【解析】解：连接、，作于， 如图,

∵六边形是正六边形，，
，，
，，
∴，
，，∴的估计值为
故答案为：．
三、解答题：本题共8小题，共66分。应写出文字说明、证明过程或演算步骤。
19．（6分）如图，方格纸中的每个小正方形的边长都为1，在建立平面直角坐标系后，的顶点均在格点上．
(1)以点A为旋转中心，将绕点A逆时针旋转90°得到，画出．
(2)画出关于原点O成中心对称的．
【解析】（1）解：如图，即为所求；3分
（2）解如图，即为所求．6分
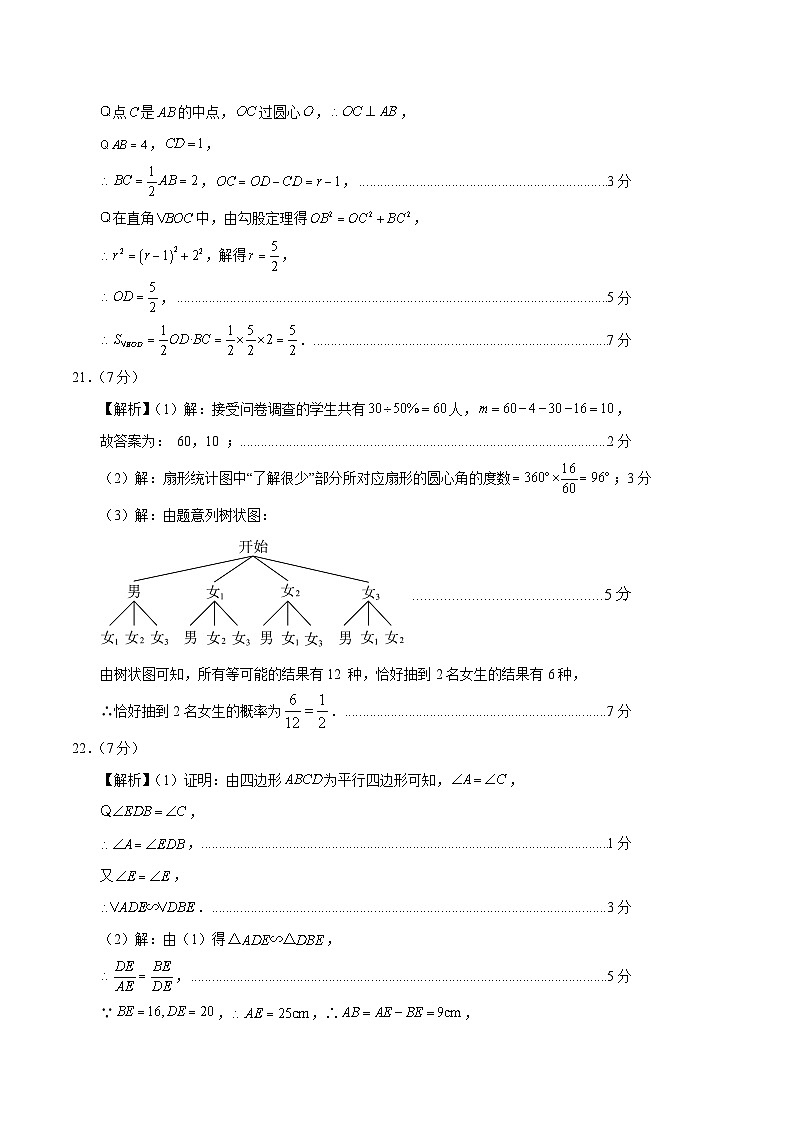
20．（7分）如图，是的一条弦，点是的中点，连接并延长交劣弧于点D，连接，．若，，求的面积．
【解析】解：设的半径是，1分
点是的中点，过圆心，，
，，
，，3分
在直角中，由勾股定理得，
，解得，
，5分
．7分
21．（7分）“校园安全”越来越受到人们的关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．根据图中信息回答下列问题：

(1)接受问卷调查的学生共有______________人，条形统计图中m的值为______________；
(2)求出扇形统计图中“了解很少”部分所对应扇形的圆心角的度数；
(3)若从对校园安全知识达到“非常了解”程度的1名男生和3名女生中随机抽取2人参加校园安全知识竟赛，请用列表或画树状图的方法，求恰好抽2名女生的概率．
【解析】（1）解：接受问卷调查的学生共有人，，
故答案为： 60，10 ；2分
（2）解：扇形统计图中“了解很少”部分所对应扇形的圆心角的度数；3分
（3）解：由题意列树状图：
5分
由树状图可知，所有等可能的结果有12 种，恰好抽到2名女生的结果有6种，
∴恰好抽到2名女生的概率为．7分
22．（7分）如图，平行四边形，交于F，交的延长线于E，且．
(1)求证：；
(2)若，，求的长．
【解析】（1）证明：由四边形为平行四边形可知，，
，
，1分
又，
．3分
（2）解：由（1）得，
，5分
∵，，∴，
在平行四边形中，．7分
23．（8分）如图，某城区公园有直径为的圆形水池，水池边安有排水槽，在正中心O处修喷水装置，喷出的水流呈抛物线状，当水管高度在处时，距离水平距离处喷出的水流达到最大高度为．
(1)求抛物线解析式，并求水流落地点B到点O的距离（即线段的长）；
(2)距离水平距离多远的E点处，放置高为的景观射灯使水流刚好到点F？
【解析】（1）解：根据题意可知，抛物线的顶点坐标为，
即设抛物线的解析式为：，1分
∵，∴，
将代入中，可得，
∴，
∴抛物线解析式为：，3分
令，可得，
∴解得（根据题意，负值舍去），
∴的坐标为，
∴，
即水流落地点B到点O的距离为；5分
（2）解：根据题意令，可得，6分
∴解得，（根据题意，负值舍去）
∴的坐标为，即，
∴点E应该与的距离为．8分
24．（9分）如图，在平面直角坐标系中，一次函数的图象与轴、轴分别交于点，与反比例函数的图象交于点．已知点坐标为，点坐标为．
(1)求，，的值；
(2)点在线段上，过点且平行于轴的直线交于点，交反比例函数图象于点．当时，求点的坐标．
【解析】（1）解：把点代入得，，
解得，
反比例函数的表达式为，2分
把点，点代入得，
解得；4分
（2）解：由（1）得反比例函数的表达式为，一次函数的表达式为；
设，
平行于轴，，
，5分
，，解得，
，7分
点的纵坐标为，
把代入得，
解得，
点的坐标为．9分
25．（10分）等腰中，，为边上一点，以为圆心的圆与相切于点，交边于，为的直径，于．
(1)如图1，求证：；
(2)如图2，延长交于，连接、，求证：．
【解析】（1）证明：如图1，连接，1分
∵切于点，∴，
∴∴，
又∵，∴，
∴，3分
∵于点，∴
∴，
∴，
∴；5分
（2）如图2，连接，6分
由（1）知，
∵，∴，∴，
∴，
∴，8分
∵，∴
又，
∴，
∵，
∴．10分
26．（12分）如图，在平面直角坐标系中，直线与抛物线的图象相交于A、B两点，点在抛物线上．
(1)求抛物线的解析式；
(2)若直线的解析式为，且的面积为35，求k的值；
(3)若，则直线必经过一个定点C，求点C的坐标．
【解析】（1）解：点在抛物线上，，解得，
抛物线的解析式为；2分
（2）解：如图所示：
由，直线过定点，
连结，
，，
轴，，4分
，
，
由，，
整理得，
由根与系数的关系得，，，6分
，
，
解得；8分
（3）解：如图所示：
设，，直线的解析式为，
，
，
由根与系数的关系得，，，9分
过点P作直线轴，分别过A、B两点作的垂线，垂足为E、F．
，，
，，
，，
，
，10分
，，
，
，
又，，
，
直线的解析式：，
直线经过定点．12分