九年级数学第三次月考卷（湖北省卷专用，人教版九上全部）2024+2025学年初中上学期第三次月考

这是一份九年级数学第三次月考卷（湖北省卷专用，人教版九上全部）2024+2025学年初中上学期第三次月考，文件包含九年级数学第三次月考卷全解全析docx、九年级数学第三次月考卷参考答案docx、九年级数学第三次月考卷考试版A4docx、九年级数学第三次月考卷考试版A3docx、九年级数学第三次月考卷答题卡A3docx、九年级数学第三次月考卷答题卡A3PDF版pdf等6份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写
在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
4．测试范围：人教版第21章一元二次方程19%+第22章二次函数28%+第23章旋转21%+第24章圆22%+第25章概率初步10%。
5．难度系数：0.68。
第一部分（选择题 共30分）
一、选择题（本大题共10小题，每小题3分，满分30分．在每个小题给出的四个选项中，只有一项符合题目要求的）
1．数学是一门美丽的学科，在平面直角坐标系内可以利用函数画出许多漂亮的曲线，下列曲线中，既是中心对称图形，也是轴对称图形的是（ ）
A．三叶玫瑰线B．四叶玫瑰线
C．心形线D．笛卡尔叶形线
【解答】解：A、是轴对称图形，但不是中心对称图形，故不符合题意；
B、既是轴对称图形，也是中心对称图形，故符合题意；
C、是轴对称图形，但不是中心对称图形，故不符合题意；
D、是轴对称图形，但不是中心对称图形，故不符合题意；
故选：B．
2．如图，AB，CD是⊙O的直径，AE=BD，若∠AOE＝32°，则∠COE的度数是（ ）
A．32°B．60°C．68°D．64°
【解答】解：∵AE=BD，
∴∠BOD＝∠AOE＝32°，
∵∠BOD＝∠AOC，
∴∠AOC＝32°
∴∠COE＝32°+32°＝64°．
故选：D．
3．下列说法正确的是（ ）
A．“明天会下雨”是必然事件
B．“概率为0.0001的事件”是不可能事件
C．测试自行车的质量应采取全面普查
D．任意掷一枚质地均匀的硬币20次，正面向上的次数不一定是10次
【解答】解：A．“明天会下雨”是随机事件，不符合题意；
B．“概率为0.0001的事件”是随机事件，不符合题意；
C．测试自行车的质量应采取抽样调查，不符合题意；
D．任意掷一枚质地均匀的硬币20次，正面向上的次数不一定是10次，正确，符合题意；
故选：D．
4．如图，在△ABC中，AB≠AC，∠BAC＝120°，将△ABC绕点C逆时针旋转，点A、B分别落在点D、E处，如果点A、D、E在同一直线上，那么下列结论错误的是（ ）
A．∠ADC＝60°B．∠ACD＝60°C．∠BCD＝∠ECDD．∠BAD＝∠BCE
【解答】解：∵将△ABC绕点C逆时针旋转，点A、B分别落在点D、E处，
∴△ABC≌△DEC，
∴CD＝CA，∠BAC＝∠EDC＝120°，得
∴∠ADC＝60°，故A正确；
∴△ADC是等边三角形，
∴∠ACD＝60°，故B正确，
∴∠DAC＝60°，∠BAE＝60°，
∵∠BCE＝∠ACD＝60°，
∴∠BAD＝∠BCE，故D正确；
∵∠ECD＝∠BCA，BC不一定平分∠ACD，
∴∠BCD不一定等于∠ECD，
故选：C．
5．若二次函数y＝﹣2x2+8x+c的图象经过A(1，y1)，B(-1，y2)，C(2+2，y3)三点，则y1、y2、y3的大小关系是（ ）
A．y2＜y3＜y1B．y1＜y3＜y2C．y1＜y2＜y3D．y2＜y1＜y3
【解答】解：将解析式转化为顶点式y＝﹣2（x﹣2）2+c+8，且﹣2＜0，
∴二次函数图象开口向下，对称轴为直线x＝2，
∴当x＜2时，y随x的增大而增大，
∵C(2+2，y3)关于对称轴的对称点为C'(2-2，y3)，
∴-1＜2-2＜1，
∴y2＜y3＜y1．
故选：A．
6．唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船的轮子被水面截得的弦AB长8m，轮子的吃水深度CD为2m，则该桨轮船的轮子半径为（ ）
A．2mB．3mC．4mD．5m
【解答】解：由题意得：AB＝8m，OC⊥AB，
∴AD＝BD=12AB＝4m，
设该桨轮船的轮子半径为r m，则OD＝（r﹣2）m，
在Rt△AOD中，由勾股定理得：42+（r﹣2）2＝r2，
解得：r＝5，
即该桨轮船的轮子半径为5m，
故选：D．
7．关于x的一元二次方程ax2+3x﹣2＝0有两个不相等的实数根，则a的值可以是（ ）
A．0B．﹣1C．﹣2D．﹣3
【解答】解：
∵关于x的一元二次方程ax2+3x﹣2＝0有两个不相等的实数根，
∴Δ＞0且a≠0，即32﹣4a×（﹣2）＞0且a≠0，
解得a＞﹣118且a≠0，
故选：B．
8．在平面直角坐标系中，二次函数y＝2x2﹣2mx+m2﹣2m（m为常数）的图象经过点（0，8），其对称轴在y轴右侧，则该二次函数有（ ）
A．最大值0B．最小值0C．最大值6D．最小值6
【解答】解：由y＝2x2﹣2mx+m2﹣2m（m为常数）的图象经过点（0，8），其对称轴在y轴右侧，
得m2﹣2m＝8，
得m＝4或﹣2（舍），
故二次函数为y＝2x2﹣8x+8＝2（x﹣2）2，
故二次函数有最小值0．
故选：B．
9．如图，在△ABC中，AB＝AC，以AC为直径的⊙O与AB，BC分别交于点D，E，连接AE，DE，若∠BED＝45°，AB＝2，则阴影部分的面积为（ ）
A．π4B．π3C．2π3D．π
【解答】解：连接OE，OD，
∵AC为⊙O的直径，
∴∠AEC＝90°，
∵AB＝AC，
∴BE＝CE，
即点E是BC的中点，
∵点O是AC的中点，
∴OE是△ABC的中位线，
∴OE∥AB，
∴S△AOD＝S△AED，
∴S阴影＝S扇形OAD，
∵∠AEC＝90°，
∴∠AEB＝90°，
∵∠BED＝45°，
∴∠AED＝45°，
∴∠AOD＝90°，
∴S扇形OAD=90π×12360=π4，
∴S阴影=π4，
故选：A．
10．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：
①abc＞0；
②3a+c＞0；
③（a+c）2﹣b2＜0；
④a+b≤m（am+b）（m为实数）．
其中结论正确的为（ ）
A．①④B．②③④C．①②④D．①②③④
【解答】解：∵抛物线开口向上，
∴a＞0，
∵抛物线对称轴为直线x=-b2a=1＞0
∴b＝﹣2a＜0，
∵抛物线与y轴交点在x轴下方，
∴c＜0
∴abc＞0，故①正确．
∵x＝﹣1时，y＝a﹣b+c＝3a+c＝0，故②不正确．
∵（a+c）2﹣b2＝（a+b+c）（a﹣b+c），
且a+b+c＜0，a﹣b+c＝0，
∴（a+c）2﹣b2＝0，故③不正确．
∵x＝1时，y＝a+b+c为最小值，
∴a+b≤m（am+b），故④正确．
故选：A．
第二部分（非选择题 共55分）
二、填空题（本大题共5小题，每小题3分，满分15分）
11．在平面直角坐标系中，若抛物线y＝x2﹣6x+c的顶点在x轴，则c的值为 ．
【解答】解：∵y＝x2﹣6x+c，
∴y＝（x﹣3）2+c﹣9，
∵抛物线y＝x2﹣6x+c的顶点在x轴，
∴c﹣9＝0，
∴c＝9．
故答案为：9．
12．如图，在⊙O中，弦BC＝2，点A是圆上一点，且∠BAC＝30°，则⊙O的半径是 ．
【解答】解：连接OB、OC，如图，
∵∠BOC＝2∠BAC＝2×30°＝60°，
而OB＝OC，
∴△OBC为等边三角形，
∴OB＝BC＝2，
即⊙O的半径为2．
故答案为：2．
13．如图，AD是正五边形ABCDE的一条对角线，以C为圆心，CB为半径画弧交AD于点F，连接CF，则∠CFD＝ °．
【解答】解：∵五边形ABCDE是正五边形，
∴∠CDE＝∠E=(5-2)×180°5=108°，AE＝DE，
∴∠EDA＝∠EAD=12（180°﹣∠E）＝36°，
∴∠CDF＝∠CDE﹣∠EDA＝108°﹣36°＝72°，
∵CF＝CD，
∴∠CFD＝∠CDF＝72°，
故答案为：72．
14．如图，一块飞镖游戏板由四个全等的直角三角形和一个正方形构成，若a＝1，b＝2．游戏板随机投掷一枚飞镖（飞镖每次都落在游戏板上），击中阴影部分的概率 ．
【解答】解：∵正方形面积为（2+1）2＝9，其中阴影部分面积为22+12＝5，
∴击中阴影部分的概率是59．
故答案为：59．
15．如图，在矩形ABCD中，AB＝4，AD＝8，Q是矩形ABCD左侧一点，连接AQ、BQ，且∠AQB＝90°，连接DQ，E为DQ的中点，连接CE，则CE的最大值为 ．
【解答】解：延长DC到点F，使CF＝DC，取AB中点O，连接FO并延长交⊙O于点Q，取CD中点G，连接OG，则OG⊥CD，
∵点E为DQ中点，点C为DF中点，
∴EC为△DQF中位线，
∵OG＝AD＝8，GF＝CG+CF＝2+4＝6，
∴OF=OG2+GF2=82+62=10，
∴QF＝QO+OF＝2+10＝12，
∵Q为圆上一动点，
∴此时FQ＝12为最大值，
∴CE的最大值为12FQ=6．
故答案为：6．
三、解答题（本大题共9小题，满分75分．解答应写出文字说明，证明过程或演算步骤）
16．（每小题3分，共6分）用适当的方法解下列一元二次方程：
（1）x（4x﹣1）＝9﹣x； （2）x2﹣6x﹣16＝0．
【解答】解：（1）x（4x﹣1）＝9﹣x，
去括号，得4x2﹣x＝9﹣x．
移项，得4x2﹣x+x＝9，
合并同类项，得4x2＝9，
开方，得2x＝±3，
解得：x1=-32，x2=32； …………………………（3分）
（2）x2﹣6x﹣16＝0，
（x﹣8）（x+2）＝0，
x﹣8＝0或x+2＝0，
解得：x1＝8，x2＝﹣2． …………………………（6分）
17．（6分）已知关于x的一元二次方程x2﹣（m﹣3）x﹣m＝0．
（1）求证：方程有两个不相等的实数根；
（2）如果方程的两实根为x1，x2，且x12+x22-x1x2=7，求m的值．
【解答】解：（1）∵方程x2﹣（m﹣3）x﹣m＝0，
a＝1，b＝﹣（m﹣3），c＝﹣m，
∴Δ＝[﹣（m﹣3）]2﹣4×1×（﹣m）
＝m2﹣6m+9+4m
＝m2﹣2m+9
＝（m﹣1）2+8＞0，
∴方程有两个不相等的实数根； …………………………（3分）
（2）由两根关系得x1+x2＝m﹣3，x1x2＝﹣m，
∵x12+x22-x1x2=7，
∴(x1+x2)2-3x1⋅x2=7，
即（m﹣3）2﹣3（﹣m）＝7，
即m2﹣3m+2＝0，
解得：m1＝2，m2＝1． …………………………（6分）
18．（6分）2024年巴黎奥运会新增了四个项目：霹雳舞，滑板，冲浪，运动攀岩，依次记为A，B，C，D，浔阳体育队的小明同学把这四个项目写在了背面完全相同的卡片上．将这四张卡片背面朝上，洗匀放好．
（1）小明想从中随机抽取一张，去了解该项目在奥运会中的得分标准，恰好抽到是B（滑板）的概率是 ．
（2）体育老师想从中选出来两个项目，让小明做成手抄报给大家普及一下，他先从中随机抽取一张不放回，再从中随机抽取一张，请用列表法或画树状图法表示出所有可能的结果，并求体育老师抽到的两张卡片恰好是B（滑板）和D（运动攀岩）的概率．
【解答】解：（1）∵一共有四张卡片，且每张卡片被抽到的概率相同，
∴小明从中随机抽取一张，恰好抽到是B（滑板）的概率是14，
故答案为：14； …………………………（2分）
（2）列表如下： （也可画树状图） …………………………（5分）
由表格可知，一共有12种等可能性的结果数，其中符合条件的结果数有2种，
∴体育老师抽到的两张卡片恰好是B（滑板）和D（运动攀岩）的概率为212=16． ………………（6分）
19．（8分）某扶贫单位为了提高贫困户的经济收入，购买了33m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m）围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．
（1）若要建的矩形养鸡场面积为90m2，求鸡场的长（AB）和宽（BC）；
（2）该扶贫单位想要建一个100m2的矩形养鸡场，这一想法能实现吗？请说明理由．
【解答】解：（1）设BC＝x m，则AB＝（33﹣3x）m，
依题意，得：x（33﹣3x）＝90，
解得：x1＝6，x2＝5．
当x＝6时，33﹣3x＝15，符合题意，
当x＝5时，33﹣3x＝18，18＞15，不合题意，舍去．
答：鸡场的长（AB）为15m，宽（BC）为6m． …………………………（4分）
（2）不能，理由如下：
设BC＝y m，则AB＝（33﹣3y）m，
依题意，得：y（33﹣3y）＝100，
整理，得：3y2﹣33y+100＝0．
∵△＝（﹣33）2﹣4×3×100＝﹣111＜0，
∴该方程无实数根，即该扶贫单位不能建成一个100m2的矩形养鸡场．…………………………（8分）
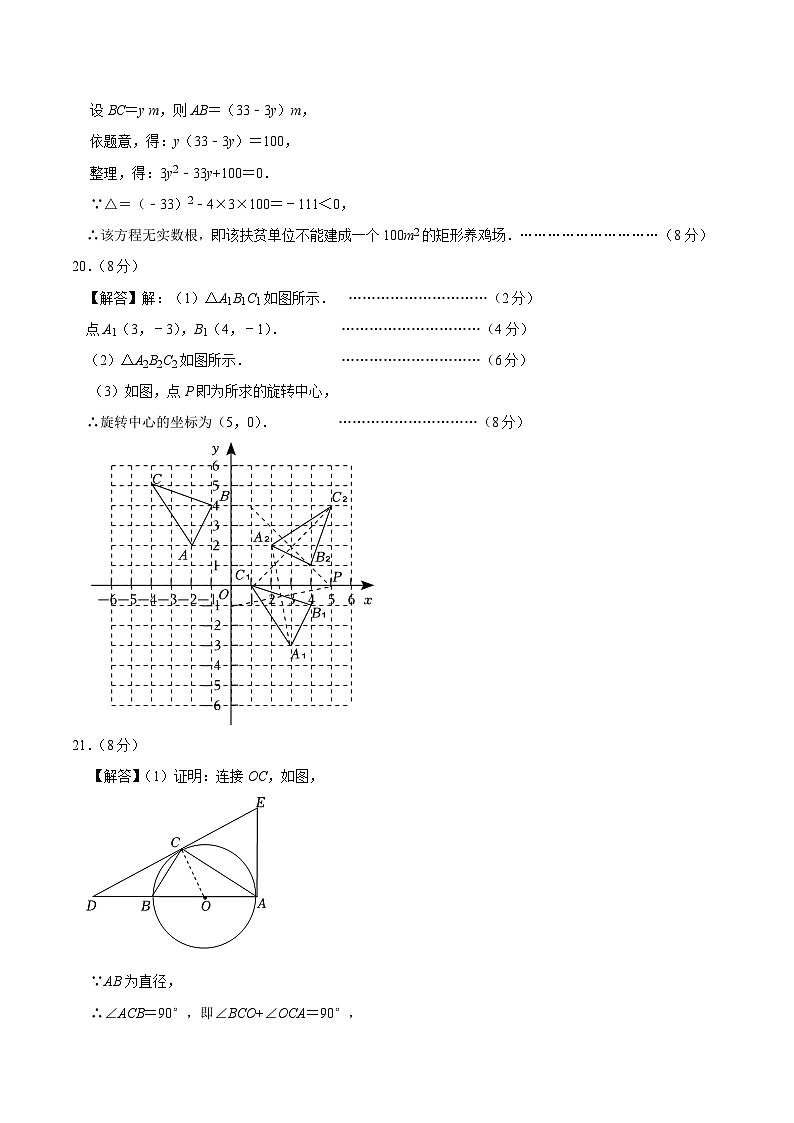
20．（8分）如图，在平面直角坐标系中，已知点A（﹣2，2），B（﹣1，4），C（﹣4，5），请解答下列问题：
（1）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（1，0）作出△A1B1C1并写出其余两个顶点的坐标；
（2）将△ABC绕点O按顺时针方向旋转90°得到△A2B2C2，作出△A2B2C2；
（3）若将△A1B1C1绕某一点旋转可得到△A2B2C2，直接写出旋转中心的坐标．
【解答】解：（1）△A1B1C1如图所示． …………………………（2分）
点A1（3，﹣3），B1（4，﹣1）． …………………………（4分）
（2）△A2B2C2如图所示． …………………………（6分）
（3）如图，点P即为所求的旋转中心，
∴旋转中心的坐标为（5，0）． …………………………（8分）
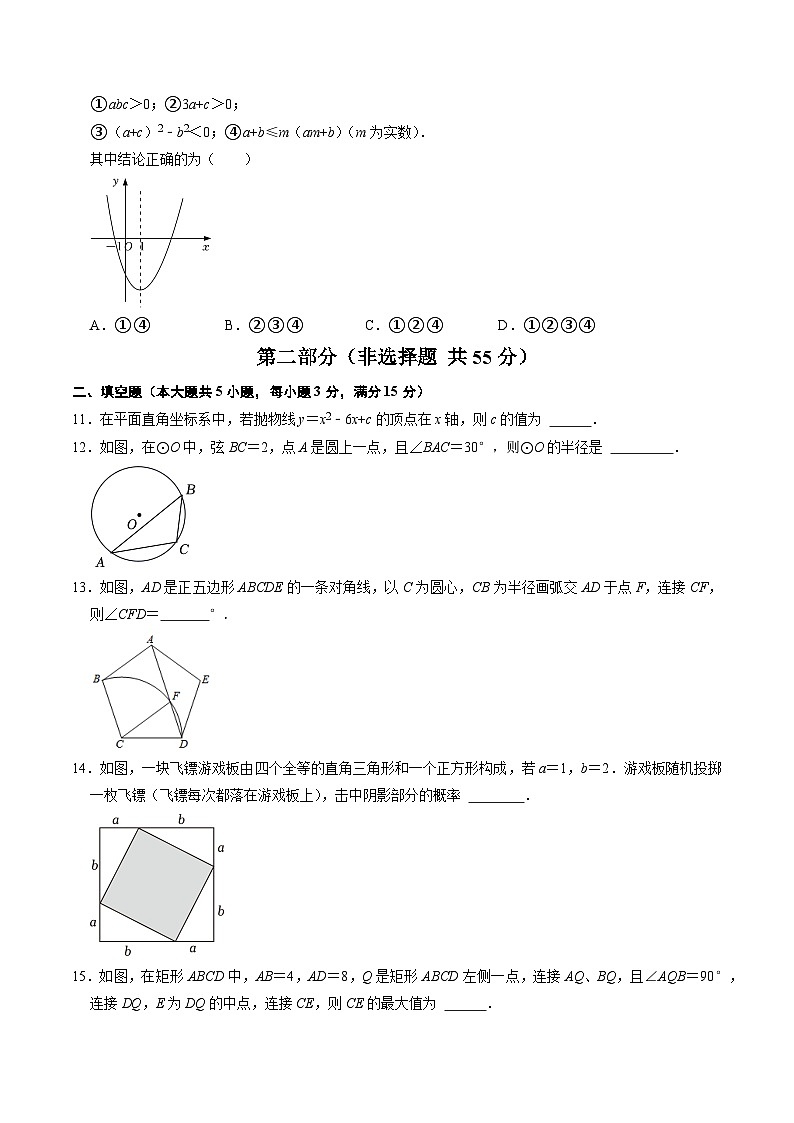
21．（8分）如图，以点O为圆心，AB长为直径作圆，在⊙O上取一点C，延长AB至点D，连接DC，
∠DCB＝∠DAC，过点A作AE⊥AD交DC的延长线于点E．
（1）求证：CD是⊙O的切线；
（2）若CD＝4，DB＝2，求AE的长．
【解答】（1）证明：连接OC，如图，

∵AB为直径，
∴∠ACB＝90°，即∠BCO+∠OCA＝90°，
又∵∠DCB＝∠CAD，∠CAD＝∠OCA，
∴∠OCA＝∠DCB，
∴∠DCB+∠BCO＝90°，
即∠DCO＝90°，
∵OC是⊙O的半径，
∴CD是⊙O的切线； …………………………（4分）
（2）解：∵∠DCO＝90°，OC＝OB，
∴OC2+CD2＝OD2，
∴OB2+42＝（OB+2）2，
∴OB＝3，
∴AB＝6，
∵AE⊥AD，AB是⊙O的直径，
∴AE是⊙O的切线，
∵CD是⊙O的切线；
∴AE＝CE，
∵AD2+AE2＝DE2，
∴（6+2）2+AE2＝（4+AE）2，
解得AE＝6． …………………………（8分）
22．（10分）网络直播销售已经成为一种热门的销售方式，某生产商在一销售平台上进行直播销售板栗．已知板栗的成本价为6元/kg，每日销售量y（kg）与销售单价x（元/kg）满足一次函数关系，下表记录的是有关数据，经销售发现，销售单价不低于成本价且不高于30元/kg．设公司销售板栗的日获利为w（元）．
（1）请求出日销售量y与销售单价x之间的函数关系式；（不用写自变量的取值范围）
（2）当销售单价定为多少时，销售这种板栗日获利w最大？最大利润为多少元？
（3）当销售单价在什么范围内时，日获利w不低于42000元？
【解答】解：（1）设y与x之间的函数关系式为y＝kx+b（k≠0），
把x＝7，y＝4300和x＝8，y＝4200代入得：
7k+b=43008k+b=4200，
解得：k=-100b=5000，
∴日销售量y与销售单价x之间的函数关系式为y＝﹣100x+5000； …………………………（3分）
（2）由题意得：
w＝（x﹣6）（﹣100x+5000）
＝﹣100x2+5600x﹣30000
＝﹣100（x﹣28）2+48400，
∵a＝﹣100＜0，对称轴为直线x＝28．
∴当x＝28时，w有最大值为48400元．
∴当销售单价定为28元时，销售这种板栗日获利w最大，最大利润为48400元；
…………………………（6分）
（3）当w＝42000元时，有：42000＝﹣100（x﹣28）2+48400，
∴x1＝20，x2＝36，
∵a＝﹣100＜0，
∴当20≤x≤36时，w≥42000，
又∵6≤x≤30，
∴当20≤x≤30时，日获利w不低于42000元． …………………………（10分）
23．（11分）已知∠AOB＝∠COD＝90°，OA＝OB＝10，OC＝OD＝8．
（1）如图1，连接AC、BD，问AC与BD相等吗？并说明理由．
（2）若将△COD绕点O逆时针旋转，如图2，当点C恰好在AB边上时，请写出AC、BC、OC之间关系，并说明理由．
（3）若△COD绕点O旋转，当∠AOC＝15°时，直线CD与直线AO交于点F，请直接写出AF的长．
【分析】（1）由“SAS”可证△AOC≌△BOD，可得AC＝BD，∠CAO＝∠DBO；
（2）连接BD，由“SAS”可证△AOC≌△BOD，可得AC＝BD，∠CAO＝∠DBO＝45°，由勾股定理可得结论；
（3）分两种情况讨论，由等腰直角三角形的性质和解直角三角形求OF的长，即可求解．
【解答】解：（1）结论：AC＝BD．
理由：∵∠AOB＝∠COD＝90°．
∴∠AOC＝∠BOD．
在△AOC和△BOD中．
OA=OB∠AOC=∠BODOC=OD，
∴△AOC≌△BOD（SAS），
∴AC＝BD； …………………………3（分）
（2）结论：BC2+AC2＝2OC2． …………………………4（分）
理由：连接BD．
∵∠AOB＝∠COD＝90°，
∴∠AOC＝∠BOD，
在△AOC和△BOD中，
OA=OB∠AOC=∠BODOC=OD，
∴△AOC≌△BOD（SAS），
∴AC＝BD∠CAO＝DBO＝45°，
∴∠CBD＝90°，
∴BC2+BD2＝CD2，
∴BC2+AC2＝2OC2； …………………………（7分）
（3）AF的长为82-10或10-863． …………………………（11分）（答对一个得2分）
（详细解答过程如下）如图3﹣1中，当点C在AO的上方时，过点O作OH⊥CD于H．
∵OC＝OD＝8，∠COD＝90°，
∴CD=2OC＝82，
∵OH⊥CD，
∴CH＝HD，
∴OH=12CD＝42，
∵∠DCO＝∠CFO+∠AOC＝45°，∠AOC＝15°，
∴∠CFO＝30°，
∴OF＝2OH＝82，
∵OA＝10，
∴AF＝OF﹣OA＝82-10．
如图3﹣2中，当点C在OA的下方时，∠OFH＝∠C+∠AOC＝60°，
∴∠FOH＝30°，
∴FH＝2OF，
∵OF2＝FH2+OH2，
∴4FH2＝FH2+（42）2，
∴FH=463，
∴OF=863，
∴AF＝AO﹣OF＝10-863，
综上所述，满足条件的AF的长为82-10或10-863．
24．（12分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，作直线BC，点P是抛物线上一个动点（点P不与点B，C重合），连接PB，PC，以PB，PC为边作平行四边形CPBD，设平行四边形CPBD的面积为S，点P的横坐标为m．
（1）求抛物线函数解析式；
（2）当点P在第四象限，且S＝6时，求点P坐标．
（3）①求S与m之间的函数关系式．
②根据S的不同取值，试探索点P的个数情况．
【解答】解：（1）抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），B（3，0），
∴抛物线的解析式为y＝（x+1）（x﹣3）＝x2﹣2x﹣3，
∴抛物线函数解析式为y＝x2﹣2x﹣3； …………………………（3分）
（2）作PQ∥y轴交直线BC于Q，如图1，
设直线BC的解析式为y＝kx+a，把C（0，﹣3），B（3，0）代入得：
b=-33k+b=0，
解得k=1b=-3，
∴直线BC的解析式为 y＝x﹣3，
设P（m，m2﹣2m﹣3），则Q（m，m﹣3），
当0＜m＜3时，如图1，PQ＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3，
S=2S△PBC=2(S△PQC+S△PQB)=212⋅3⋅(-m2+3m)=-3m2+9m，
∵S＝6，
∴﹣3m2+9m＝6，
解得：m1＝1，m2＝2，
∴点P的坐标为（1，﹣4）或（2，﹣3）； …………………………（7分）
（3）①由（2）得当0＜m＜3时，S＝﹣3m2+9m；
当 m＜0或m＞3时，如图2，
PQ＝m2﹣2m﹣3﹣（m﹣3）＝m2﹣3m，
∴S=2S△PBC=2(S△PBQ-S△PQC)=2×12⋅3⋅(m2-3m)=3m2-9m，
综上所述：S=-3m2+9m(0＜m＜3)3m2-9m(m〈0或m〉3)； …………………………9（分）
②当0＜m＜3时，S=-3m2+9m=-3(x-32)2+274，
S关于x的函数图象如图3所示，
∴当S＞274时，点P的个数有两个； …………………………（10分）
当S=274时，点P的个数有三个 ； …………………………（11分）
当0＜S＜274时，点P的个数有四个． …………………………（12分）A
B
C
D
A
（B，A）
（C，A）
（D，A）
B
（A，B）
（C，B）
（D，B）
C
（A，C）
（B，C）
（D，C）
D
（A，D）
（B，D）
（C，D）
x（元/kg）
7
8
9
y（kg）
4300
4200
4100