广东省深圳市福田区联考2024-2025学年九年级上学期期中考试数学试卷-A4

这是一份广东省深圳市福田区联考2024-2025学年九年级上学期期中考试数学试卷-A4，共7页。试卷主要包含了选择题等内容，欢迎下载使用。
1．下列图形中，不是相似图形的一组是
A．B．
C．D．
2．若正方形的边长为1，则该正方形的对角线长为
A．1B．C．2D．4
3．方程的解是
A．，B．，C．，D．，
4．若，，，是成比例线段，其中，，，则线段的长为
A．2B．3C．4D．6
5．下列说法正确的是
A．菱形的对角线相等B．四个内角都相等的四边形是矩形
C．有一组邻边相等的菱形是正方形D．两条对角线垂直且平分的四边形是正方形
6．如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图，在点处放一水平的平面镜，光线从点出发经平面镜反射后刚好射到古城墙的顶端处，已知，，且测得，，，那么该古城墙的高度是
A．B．C．D．
7．《代数学》中记载，形如的方程，求正数解的几何方法是：“如图1，先构造一个面积为的正方形，再以正方形的边长为一边向外构造四个面积为的矩形，则阴影部分的面积为．因为大正方形的面积为，结合图1，则该方程的正数解为．”小皓按此法解关于的方程时，构造出如图2所示的图形，已知阴影部分的面积为64，则该方程的正数解＝
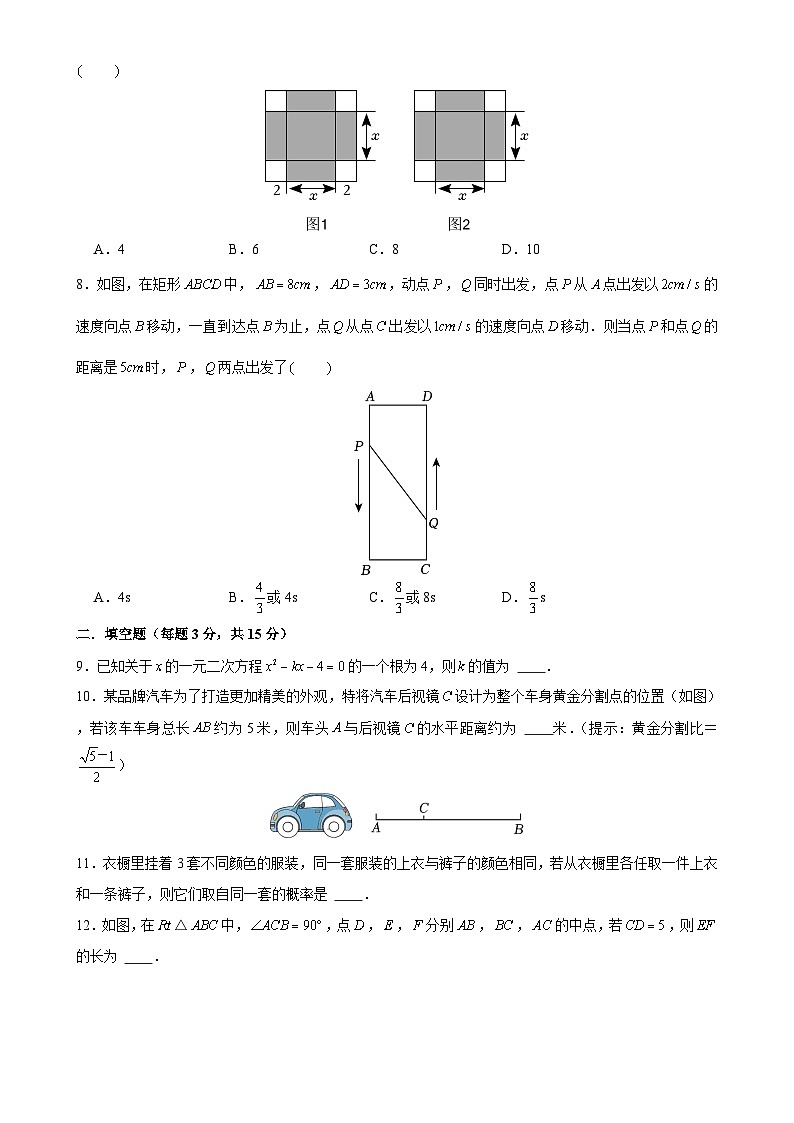
A．4B．6C．8D．10
8．如图，在矩形中，，，动点，同时出发，点从点出发以的速度向点移动，一直到达点为止，点从点出发以的速度向点移动．则当点和点的距离是时，，两点出发了
A．4sB．或4sC．或8sD．s
二．填空题（每题3分，共15分）
9．已知关于的一元二次方程的一个根为4，则的值为 ．
10．某品牌汽车为了打造更加精美的外观，特将汽车后视镜设计为整个车身黄金分割点的位置（如图），若该车车身总长约为5米，则车头与后视镜的水平距离约为 米．（提示：黄金分割比＝）
11．衣橱里挂着3套不同颜色的服装，同一套服装的上衣与裤子的颜色相同，若从衣橱里各任取一件上衣和一条裤子，则它们取自同一套的概率是 ．
12．如图，在△中，，点，，分别，，的中点，若，则的长为 ．
13．如图，在中，，，点，分别在，上，，，交于点，则的面积的最大值是 ．
三．解答题（共61分）
14．（6分）解方程：
（1）；（2）．
15．（7分）某校为了解九年级学生对深圳哪类研学内容最感兴趣（每人仅能选一类）．源远流长的饮食文化；．享誉世界的改革开放文化；．可歌可泣的抗战文化；．感天动地的移民文化．从九年级学生中随机抽取若干名学生进行调查，绘制了如图所示的统计表和扇形统计图（均不完整）．
抽取的学生最感兴趣研学内容统计表
请根据以上信息，解答下列问题：
（1）填空： ， ， （请填小数）；
（2）若该校九年级共有540名学生，估计选择“．可歌可泣的抗战文化”的有多少人？
（3）小聪和小睿参加了本次调查，请你用列表或画树状图的方法求他们选择同一类内容的概率．
16．（7分）如图，在平面直角坐标系中，△的顶点坐标分别为，，．
（1）画出将△向左平移2个单位长度，再向上平移1个单位长度后得到的△；
（2）以原点为位似中心，在轴的右侧画出△的一个位似△，使它与△的相似比为；
（3）判断△和△_____位似图形（填“是”或不是），若是，请在图中标出位似中心点，并写出点的坐标．
17．（8分）如图，在中，分别是，的中点，，延长到点，使得，连．
（1）求证：四边形是菱形；
（2）若，，求菱形的面积．
18．（9分）根据以下素材，探索完成任务．
19．（9分）【项目学习】配方法是数学中一种常见的解题方法，利用配方法可求一元二次方程的根，所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，其实这种方法还经常被用到代数式的变形中并结合非负数的意义解决某些问题．
例1：把代数式进行配方．
解：原式．
例2：求代数式的最大值．
解：原式．
∵，∴．∴．
∴代数式的最大值为．
【问题解决】
（1）若m，k，h满足，求的值．
（2）若△ABC的三边长a，b，c均为整数，c＝3，a，b满足，求△ABC的周长．
【迁移应用】
（3）如图，有一块锐角三角形余料，它的边厘米，高厘米．现要用它裁出一个矩形工件，使矩形的一边在上，其余的两个顶点分别在、上．
①设，试用含的代数式表示矩形工件的面积；
②运用“配方法”求的最大值．
20．（12分）综合与实践
【问题解决】活动课上，同学们以正方形为背景，探究图形运动中的数学结论，各小组精心设计一些题目，选取以下3个图形进行研究，已知正方形中，，点是射线上的一个动点，连接，以为边作正方形（点在边所在直线的上方），连接．
【探索发现】
（1）如图1，“会学习”小组画出了点与点重合时的图形，此时点到边所在直线的距离＝ ．
（2）如图2，“勤探究”小组画出点恰好是线段中点时的图形，请解答如下问题：
①判断线段与的数量关系，并说明理由；
②写出此时点到边所在直线的距离，并说明理由．
【拓展延伸】如图3，“能合作”小组画出了点在线段延长线上时的图形，与交于点P．若点P是线段AE的三等分点，请直接写出此时DE的长．

研学内容
人数
频率
24
0.4
9
素材1
某校统一安装了日光灯，日光灯中最易损坏的是灯管和镇流器．
素材2
该校后勤部准备补进灯管和镇流器共400件．批发市场灯管的单价为30元，镇流器的单价为80元．商家为了促销且保证有一定的利润，当镇流器购买数量超过80件时，每多购买1件，单价下降1元，但单价不低于50元．
问题解决
任务1
若镇流器补进90件，则学校补进镇流器和灯管共多少元？
任务2
设镇流器补进件，若，刚补进镇流器的单价为 元，补进灯管的总价为 （用含的代数式表示，结果要求最简）；
任务3
若学校后勤部补进镇流器和灯管共花15000元，求补进镇流器多少件？