广东省部分学校2024-2025学年高三上学期11月联考数学试题 -

这是一份广东省部分学校2024-2025学年高三上学期11月联考数学试题 -，文件包含2025届广东省高三联考数学1128-2024docx、数学答案docx、1128广东联考数学答案pdf、2025届广东省高三联考数学1128pdf等4份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

2. B 由 x+3>0 ,得 x>−3 ,则 A=−3,+∞ ,由 x2+2x−3≥0 ,得 x≤−3 或 x≥1,B= −∞,−3]∪[1,+∞,A∩B=[1,+∞) .
3. D 由 y=x2−2ex ,得 y′=x2+2x−2ex . 当 x=0 时, y=−2,y′=−2 ,故曲线 y=x2 −2)ex 在 x=0 处的切线方程为 2x+y+2=0 .
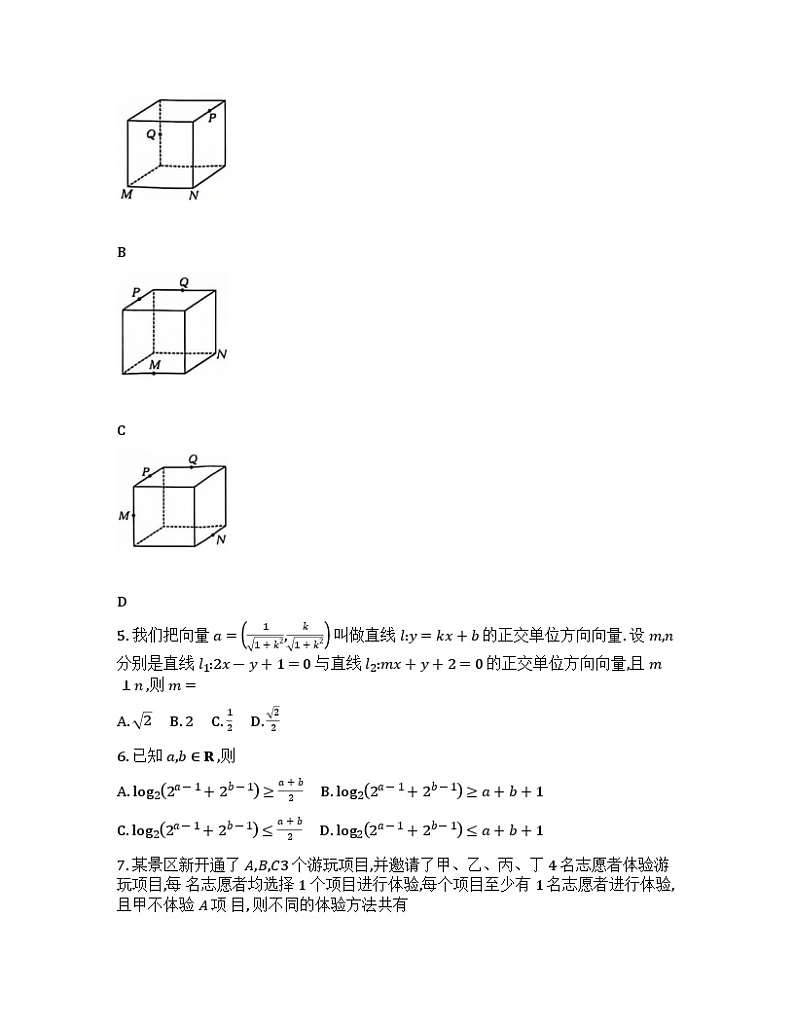
4. D 由 D 选项的图可知, M,N,P,Q 四点共面,由 A,B,C 选项的图可知, M,N,P,Q 四点均不共面.
5. C 由题意可知 m=15,25,n=11+m2,−m1+m2 ,因为 m⊥n ,所以 15×11+m2+25 ×−m1+m2=0 ,解得 m=12 .
6. A 因为 2a−1+2b−1≥22a−1⋅2b−1=2a+b2 ,当且仅当 a=b 时,等号成立,所以 lg22a−1+2b−1≥lg22a+b2=a+b2.
7. C 若乙、丙、丁 3 人体验的项目各不相同,则有 C21 A33=12 种体验方法,若乙、丙、丁 3 人有 2 人体验的项目相同,则有 C21C32 A22=12 种体验方法,故不同的体验方法共有 24 种.
8. B 由题可得 gx=sin2ωx−ωπ6+π3 ,因为 ω>0 ,所以当 0π3 ,所以 −ωπ6+π3≥−π2,ωπ2+π3≤π2, 解得 0<ω≤13 .
9. ABD 因为 X∼N0,1 ,所以 φ0=PX≥0=12, A 正确. 显然 φx 是减函数, B 正确. 因为 φ−x+φx=PX≥−x+PX≥x=1 ,且 φ−x≠φx ,所以 φx 不是偶函数, φx 的图象关于点 0,12 对称, C 不正确, D 正确.
10. AD 若 fx 为偶函数,则由 f−1=f1 ,得 1m×−3n=3m×−1n ,则 3m=3n ,从而 m=n , A 正确. 若 m+n=3 ,由 m,n∈N* ,得 m=1,n=2 或 m=2,n=1. 当 m=1,n=2 时, fx=(x+ 2)x−22,f′x=3x2−4x−4=3x+2x−2 . 由 f′x=0 ,得 x=−23 或 x=2 ,则
fx 有 2 个极值点, B 不正确. 若 m=n+2 ,不妨取 m=3,n=1, 此时 fx=x+23x−2 ,则 f−3=−13×−5=5>0,C 不正确. 当 x>2,m≥2 时, fxx−2n=x+2m=xm+ Cm1xm−1×21+Cm2xm−2×22+⋯+Cmm×2m . 因为 x>2 ,所以 Cm2xm−2×22+⋯+Cmm×2m>0 , 则 fxx−2n=x+2m>xm+Cm1xm−1×21=xm+2mxm−1=xm1+2mx,D 正确.
11. ACD 因为 an 是正项数列,所以 a2025=a2024a2024−1>0,a2024>0, 则 a2024>1, A 正确. 若 an=2 ,满足 an+1=anan−1, B 不正确. Tn+2Tn=an+1⋅an+2=an+12an+1−1=an+1+an+1an+1−1=an+1+an+2=Sn+2 −Sn,C 正确.
因为 an+an+1=an+anan−1=an−1+1an−1+2≥2an−1⋅1an−1+2=4 ,
当且仅当 an−1=1an−1 ,即 an=2 时,等号成立,所以 S2n=i=1na2i−1+a2i≥i=1n4=4n ,当且仅当 a1=a2=⋯=a2n−1=a2n=2 时,等号成立. 同理可得 T2n≥4n ,当且仅当 a1=a2=⋯= a2n−1=a2n=2 时,等号成立,故 S2n+T2n≥4n+4n,D 正确.
12. 2+i 由 z=1+2ii=2−i ,得 z=2+i .
13. 2−3 由 cs2α=4sinα+π4 ,得 csα+sinαcsα−sinα=22csα+sinα . 因为 csα−sinα≤2 ,所以 csα+sinα=0 ,即 tanα=−1 ,则 tanα+π3=tanα+tanπ31−tanα⋅tanπ3=2−3.
14. 22−2 由题可知 l1 过定点 A0,1,l2 过定点 B0,5 ,且 l1⊥l2 ,故点 P 的轨迹是以 M0,3 为圆心,2 为半径的圆 (点 N0,1 除外). 设 Q2t,t2,PQ≥QM−2=2t2+t2−32−2=t2−12+8−2≥22−2.
15. 解:(1)由表格数据可知 30 名女员工中, BMI 值处于肥胖等级的有 6 人,则估计该单位女员工的 BMI 值处于肥胖等级的概率 P=630=15 . 2 分
在该单位任选 3 名女员工,则这 3 人中至少有 1 人的 BMI 值处于肥胖等级的概率 P1= 1−1−P3=1−453=61125. 6 分
(2) 2×2 列联表如下:
7 分
零假设为 H0 : 该单位员工的性别与肥胖之间无关联. 8 分
χ2=nad−bc2a+bc+da+cb+d=80×24×14−6×36220×60×30×50=0.64<6.635=x0.01, 11 分
根据小概率值 α=0.01 的独立性检验,没有充分证据推断 H0 不成立,因此可以认为 H0 成立,即认为该单位员工的性别与肥胖之间无关联. 13 分
16. 解:(1) 由 bcsC+acsB−c=0 ,得 sinBcsC+sinAcsB−sinC=0 . 1 分
因为 sinC=sinA+B=sinAcsB+csAsinB , 3 分
所以 sinBcsC−sinBcsA=sinBcsC−csA=0 . 4 分
又 sinB≠0 ,所以 csC−csA=0 , 5 分
则 A=C ,从而 △ABC 是等腰三角形. 6 分
(2)因为 A=C ,所以 a=c . 7 分
由余弦定理知 b2=a2+c2−2accsB , 8 分
因为 b=4 ,所以 16=2a2−2a2csB ,得 a2=81−csB . 9 分
△ABC 的面积 S=12acsinB=12a2sinB=4sinB1−csB=8sinB2csB22sin2B2=4tanB2 . 11 分
因为 △ABC 为锐角三角形,所以 0则 04 , 14 分
故 △ABC 面积的取值范围为 4,+∞ . 15 分
17. (1) 证明:取 BC 的中点 M ,连接 AM,DM .
因为 AB=AC,BD=CD ,所以 AM⊥BC,DM⊥BC , 1 分
从而 BC⊥ 平面 ADM . 2 分
又 AD⊂ 平面 ADM ,所以 AD⊥BC . 3 分
因为 AD⊥BD,BC∩BD=B ,所以 AD⊥ 平面 BCD . 4 分
又 CD⊂ 平面 BCD ,所以 CD⊥AD . 5 分
因为 CD⊥BD,BD∩AD=D ,所以 CD⊥ 平面 ABD . 6 分
又 AB⊂ 平面 ABD ,所以 AB⊥CD . 7 分
(2)解:由(1)可知, DA,DB,DC 两两垂直,设 AD=a,BD=b ,由 BE=EF=FC ,得 d1=d3=b3,AM=AD2+DM2=a2+b22=4a2+2b22,S△ABC=12AM⋅BC= b2a2+b22,VA−BCD=13S△BCD⋅AD=13×12b2a=ab26,VD−ABC=13S△ABC⋅d2=b2a2+b26d2=ab26 ,则 d2=ab2a2+b2 . 10 分
由 1d12+6d22=3d32 ,得 18b2=62a2+b2a2b2 ,则 a=b . 以 D 为坐标原点, DB,DC,DA 所在直线分别为 x 轴, y 轴, z 轴,建立如图所示的空间直角坐标系,则 E2b3,b3 , 0),A0,0,b,D0,0,0,C0,b,0,AE=2b3,b3,−b,CD=(0 , −b,0) . 12 分

cs⟨AE,CD⟩=AE⋅CDAECD=−b2314b23=−1414, 14 分
故直线 AE 与 CD 所成角的余弦值为 1414 . 15 分
18. (1) 解:由题可知, M0,a,N0,−a ,设 Px0,y0,x0≠0 , 1 分
则 kPM⋅kPN=y0−ax0⋅y0+ax0=y02−a2x02=−43 , 2 分
整理得 y02a2+4x023a2=1 . 3 分
因为点 P 在 C 上,所以 3a24=3 ,解得 a2=4 ,故 C 的方程为 y24+x23=1 . 4 分
(2)①证明:由(1)可知 F0,1 ,则 l:y=kx+1 ,设 Ax1,y1,Bx2,y2 .
联立方程组 y24+x23=1,y=kx+1, 整理得 3k2+4x2+6kx−9=0 , 5 分
则 x1+x2=−6k3k2+4,x1x2=−93k2+4 . 6 分
因为点 A 关于 x 轴对称的点为 D ,所以 OD2=OA2=x12+y12=x12+kx1+12=(1+ k2⋅x12+2kx1+1, 7 分
同理可得 OB2=1+k2x22+2kx2+1 ,则 OD2−OB2=x1−x21+k2x1+x2+
2k]=2kx1−x23k2+4. 8 分
因为点 A 在第一象限内, k>0 ,所以 x1−x2>0 ,则 2kx1−x23k2+4>0 ,从而 OD2−OB2>0 ,
即 OD>OB . 10 分
②解:因为 k=1 ,所以 x1+x2=−67 ,则线段 AB 的中点为 G−37,47 , 11 分
线段 AB 的垂直平分线的方程为 y=−x+17 . 12 分
由 A,D 两点关于 x 轴对称,可得过 A,B,D 三点的圆的圆心在 x 轴上,令 y=0 ,得 x=17 ,即
过 A,B,D 三点的圆的圆心为 Q17,0 . 13 分
AB=1+k2x1+x22−4x1x2=247,GQ=17+372+472=427, 15 分
设过 A,B,D 三点的圆的半径为 r ,则 r2=AB22+GQ2=17649 , 16 分
则过 A,B,D 三点的圆的方程为 x−172+y2=17649 . 17 分
19. (1) 证明:假设 fx=sinx 是类周期函数,且 TT>0 为 fx 的一个类周期,
则由 fx+T=T⋅fx ,得 sinx+T=Tsinx . 1 分
令 x=0 ,得 sinT=0 ,从而 T=kπ,k∈N* . 2 分
若 k 为奇数,则由 sinx+T=Tsinx ,得 −sinx=kπsinx ,即 kπ+1sinx=0 ① 3 分
若 k 为偶数,则由 sinx+T=Tsinx ,得 sinx=kπsinx ,即 kπ−1sinx=0 ②. 4 分
①,②式不可能恒成立,故假设不成立,从而 fx=sinx 不是类周期函数. 5 分
(2)解:因为 2 是函数 fx 的一个类周期,所以 fx+2=2fx . 6 分
令 x=0 ,则 f2=2f0=2 . 7 分
令 x=2n ,则 f2n+2=2f2n ,即 an+1=2an . 8 分
因为 a1=f2=2 ,所以 an 是首项为 2 ,公比为 2 的等比数列, 9 分
则 Sn=21−2n1−2=−2+21−2n=2+22n−1 . 10 分
(3) 解:设 fx=ax 的类周期为 T ,则由 fx+T=T⋅fx ,得 ax+T=T⋅ax ,则 aT− T=0 .
(方法一) 由 aT−T=0,a≠1 ,得 Tlna=lnT ,即 lna=lnTT . 11 分
令 gx=lnxx,x>0 ,则 g′x=1−lnxx2 . 12 分
当 x∈0,e 时, g′x>0,gx 单调递增; 当 x∈e,+∞ 时, g′x<0,gx 单调递减. 13 分
若 gxmax=ge=1e , 14 分
从而 lna≤1e ,解得 0即 a 的取值范围为 0,1∪1,e1e . 17 分
(方法二) 令 gx=ax−x ,由题意可知 gx 在 0,+∞ 上存在零点, g′x=axlna−1 . 11 分
若 00,g1=a−1<0 ,所以 gx 在(0,1)上存在零点,符合题意. 12 分
若 a>1 ,则 lna>0 ,由 g′x=0 ,得 x=−lgalna . 13 分
若 a≥e ,则 −lgalna<0 ,当 x∈−∞,−lgalna 时, g′x<0,gx 单调递减,当
x∈−lgalna,+∞ 时, g′x>0,gx 单调递增,从而当 x∈0,+∞ 时, gx>g0= 1,故 gx 在 0,+∞ 上不存在零点,不符合题意. 14 分
若 10 ,当 x∈−∞,−lgalna 时, g′x<0,gx 单调递减,当
x∈−lgalna,+∞ 时, g′x>0,gx 单调递增,从而当 x∈0,+∞ 时, gx≥ g−lgalna=1lna+lgalna. 15 分
由 gx 在(0,1)上存在零点,得 1lna+lgalna≤0 ,则 lna≤a−lgae=1e ,则 a≤e1e ,从而 1综上, a 的取值范围为 0,1∪1,e1e . 17 分肥胖
不肥胖
总计
女员工
6
24
30
男员工
14
36
50
总计
20
60
80