贵州省仁怀市第四中学2024-2025学年高一上学期期中检测数学试题

这是一份贵州省仁怀市第四中学2024-2025学年高一上学期期中检测数学试题，共6页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的．
1．命题“”的否定是（ ）
A．B．
C．D．
2．若全集，设集合．则（ ）
A．B．C．D．
3．设，则“”是“”的（ ）
A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件
4．下列图象中，表示定义域、值域均为的函数是（ ）
A．B．C．D．
5．不等式的解集为（ ）
A．B．C．D．
6．已知函数，则下列结论中正确的是（ ）
A．B．在上单调递减
C．是偶函数D．若，则为
7．已知函数在闭区间上有最大值3，最小值2，则的取值范围是（ ）
A．B．C．D．
8．若函数为奇函数，则（ ）
A．B．C．D．1
二、多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求．
9．下列函数中，既是偶函数，又在上单调递减的是（ ）
A．B．C．D．
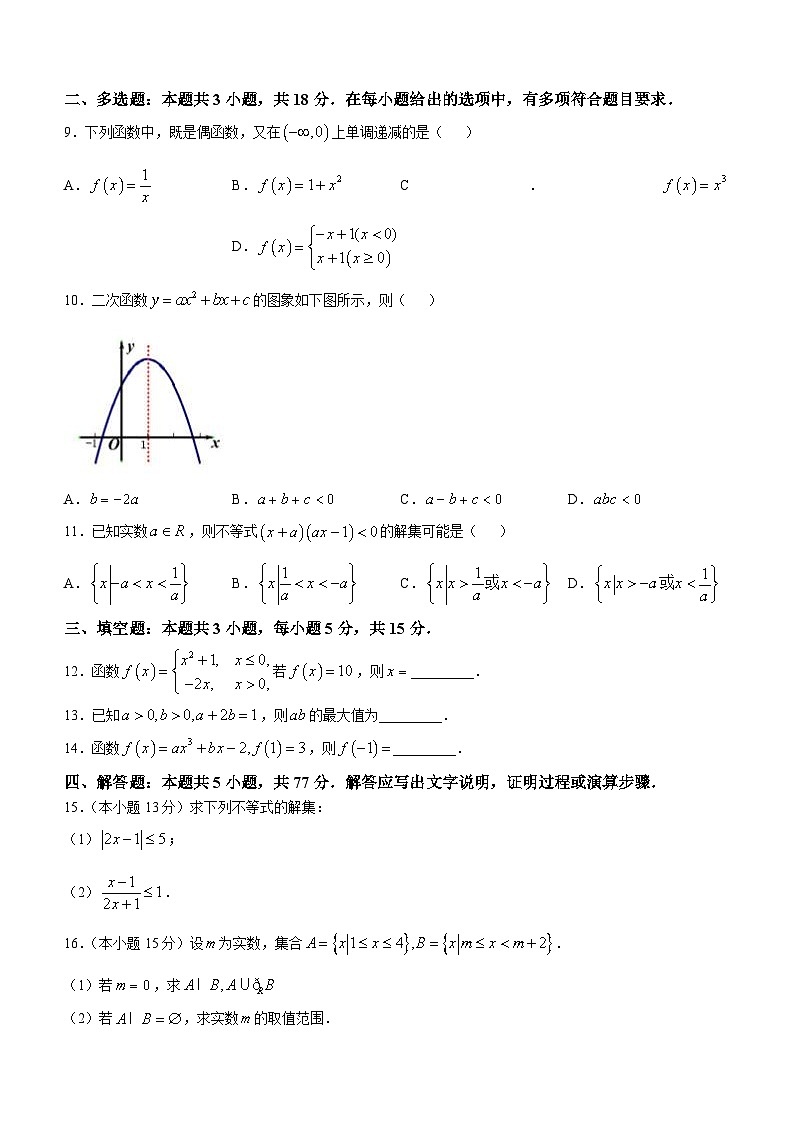
10．二次函数的图象如下图所示，则（ ）
A．B．C．D．
11．已知实数，则不等式的解集可能是（ ）
A．B．C．D．
三、填空题：本题共3小题，每小题5分，共15分．
12．函数若，则_________．
13．已知，则的最大值为_________．
14．函数，则_________．
四、解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．
15．（本小题13分）求下列不等式的解集：
（1）；
（2）．
16．（本小题15分）设为实数，集合．
（1）若，求
（2）若，求实数的取值范围．
17．（本小题15分）已知函数
（1）判断并证明函数的奇偶性；
（2）判断并证明函数在上的单调性．
18．（本小题17分）设二次函数．
（1）若函数的零点为，求函数；
（2）若，求的最小值．
19．（本小题17分）函数在区间上的最小值记为．
（1）求的函数解析式；
（2）求的最大值．
仁怀四中2024—2025年度第一学期半期考试
高一数学答案
一、单选题（40分）
二、多选题（18分）
三、填空题（15分）
12． 13． 14．
三、解答题（77分）
15．解：（1）由可得，，解得，
所以不等式的解集为．
（2）由可得，
化简得：，即，解得或，
所以不等式的解集为．
16．解：（1）当时，集合，
，
．
（2）集合，
或，解得或，
实数的取值范围是．
17．解：（1）函数的定义域为，
，
为奇函数；
（2）在区间上为增函数；
证明：任取，且，
则，
因为，所以，
所以，即在区间上为增函数．
18．解：（1）根据题意，二次函数，
若函数的零点为和2，
则方程的两根为和2，
则有，解可得，
则，
（2）若，则，
则
，
当且仅当时等号成立，
则的最小值为9．
19．解：（1）①当时，函数图象的对称轴为，则；
②当时，函数图象的对称轴为，则；
③当时，函数图象的对称轴为，则．
综上所述，
（2）①当时，由（1）知；
②当时，由（1）知；
③当时，由（1）知．
综合①②③可得．题号
1
2
3
4
5
6
7
8
答案
A
A
B
C
D
B
D
A
题号
9
10
11
答案
BD
ACD
AD