福建省平和广兆中学2023-2024学年高二上学期10月月考数学试卷

这是一份福建省平和广兆中学2023-2024学年高二上学期10月月考数学试卷，共9页。试卷主要包含了请将答案正确填写在答题卡上，已知数列的通项公式为，则，已知等差数列，若，则公差为，等差数列中，，求，已知数列对任意满足，则，下列数列是等比数列的是，数列的前n项和为，已知，则等内容，欢迎下载使用。
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
一、单选题：本大题共8个小题，每个小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的．
1．数列的一个通项公式可以是（ ）
A． B． C． D．
2．在递减等比数列中，，则（ ）
A．16 B． C．4 D．
3．已知数列的通项公式为，则（ ）
A．12 B．14 C．16 D．18
4．已知等差数列，若，则公差为（ ）
A． B．4 C．1 D．2
5．等差数列中，，求（ ）
A．36 B．15 C．18 D．30
6．已知是等差数列的前n项和，若，则（ ）
A．15 B．20 C．25 D．
7．已知等比数列的前n项和为，且，则（ ）
A．4 B．3 C．2 D．1
8．已知数列对任意满足，则（ ）
A．4040 B．4043 C．4046 D．4049
二、多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
9．下列数列是等比数列的是（ ）．
A．1，1，1，1，1 B．0，0，0，0，…… C． D．，1，，…
10．数列的前n项和为，已知，则（ ）
A．是递减数列 B．
C．当时， D．当时，取得最大值
11．在7和21之间插入个数，使这个数成等差数列，则该等差数列的公差可以是（ ）
A． B．7 C．5 D．3
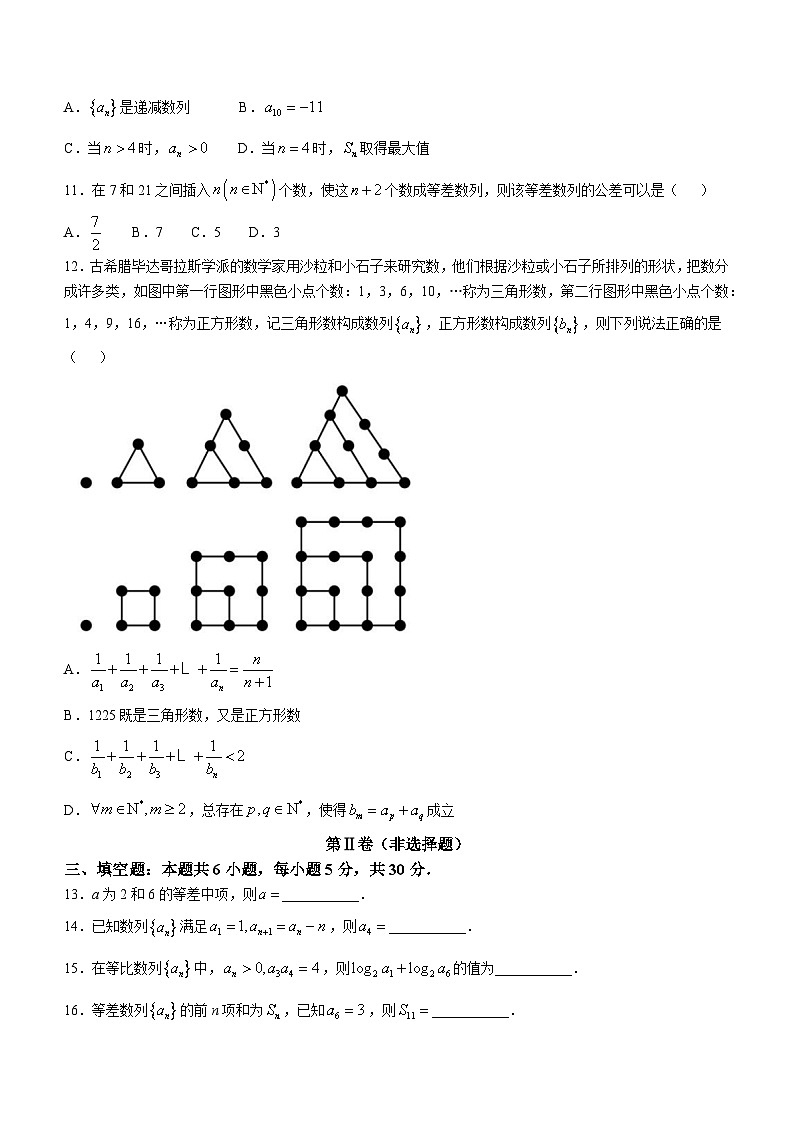
12．古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图中第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列，正方形数构成数列，则下列说法正确的是（ ）
A．
B．1225既是三角形数，又是正方形数
C．
D．，总存在，使得成立
第Ⅱ卷（非选择题）
三、填空题：本题共6小题，每小题5分，共30分．
13．a为2和6的等差中项，则___________．
14．已知数列满足，则___________．
15．在等比数列中，，则的值为___________．
16．等差数列的前n项和为，已知，则___________．
17．若数列满足则数列的通项公式___________．
18．设为数列的前n项和，，且．记为数列的前n项和，若，则m的最小值为___________．
四、解答题：本小题共5小题，共60分．解答应写出文字说明、证明过程或演算步骤．
19．（10分）设是等比数列，
（1）求的通项公式；
（2）求
20．（12分）记为等差数列的前n项和，已知．
（1）求公差d及的通项公式；
（2）若，并求n的值．
21．（12分）已知数列的前n项和，且；
（1）求它的通项
（2）若，求数的前n项和．
22．（12分）已知数列满足．
（1）求的通项公式；
（2）若，求数列的前n项和．
23．（14分）若数列的前n项和满足：，记．
（1）求数列的通项公式；
（2）若，求证：；
（3），求的值．（注：表示不超过x的最大整数，例：）
202310广兆中学高二（上）数学月考参考答案：
1．D 2．C 3．D 4．D 5．A 6．B 7．C 8．B 9．AC 10．ABD． 11．AB 12．BCD
13．4 14． 15．2 16．33． 17． 18．
19．（共10分）
【详解】（1）设等比数列的公比为q，所以， 2分
因为，所以； 5分
（2）由（1）得
所以 10分
20．（共12分）
【详解】（1）设的公差为d，由题意得．
由得 2分
所以的通项公式为 6分
（2）由（1）得， 10分
所以 12分
21．（共12分）
【详解】（1），∴当时，， 1分
当时，，经验证，满足， 5分
； 6分
（2），
∴数列是以首项为1，2为公比的等比数列， 7分
8分
12分
22．（共12分）
【详解】（1）由，
得当时，即， 1分
当时，， 2分
则，即， 4分
当时，也满足上式，
综上所述，； 6分
（2）由（1）得，
则， 8分
所以 10分
12分
23．（共10分）
【分析】（1）由先求出，从而可求出；
（2）由累加法及错位相减法求出数列的通项公式，即可证明不等式成立；
（3）由，进行放缩可得，从而得到，可求得．
【详解】解：（1）当时，，解得， 1分
当时，，即．
所以数列是以为首项，公比为2的等比数列．
， 3分
从而； 4分
（2）由（1）知，
即， 5分
当时，记，
则，
两式相减得
7分
所以，
即，当时，也符合上式，
所以； 9分
（3）由（1）知，
由，
得，
即， 12分
所以，
所以 14分
【小题部分解析】
7．C 【详解】当时，，
当时，，
故当时，，
因为数列为等比数列，易知该数列的公比为2，则，即，
解得．
8．B 【详解】由可得；
两式相减可得；
即相邻的奇数项或者偶数项成等差数列，且公差为4，
所以可得，即；
当时，，因此．
11．AB 【分析】根据给定条件，用n表示出等差数列的公差，再分析判断作答．
【详解】依题意，这个等差数列的公差，
当时，，B符合；当时，，A符合；
显然不存在正整数n，使得d取5和取3，CD不符合．
故选：AB
12．BCD 【分析】根据给定信息，求出数列的通项，再逐一分析各个选项即可判断作答．
【详解】依题意，数列中，，
于是得满足上式，
数列中，，
于是得满足上式，
因此，
对于A，，则，A不正确；
对于B，因为，则，又，则，B正确；
对于C，，
则，C正确；
对于D，，取，则
，
所以，总存在，使得成立，D正确．
故选：BCD
17．【详解】解：
18． 【分析】先对条件变形，构造等比数列，求出，再分组求和得到，求出，利用等比数列求和公式求解出，求出m的最小值
【详解】等式两边同除以得：，
由得：，
因为，所以，解得：，
∴数列是以为首项，以为公比的等比数列，
则，
，
．
，
的最小值为．