








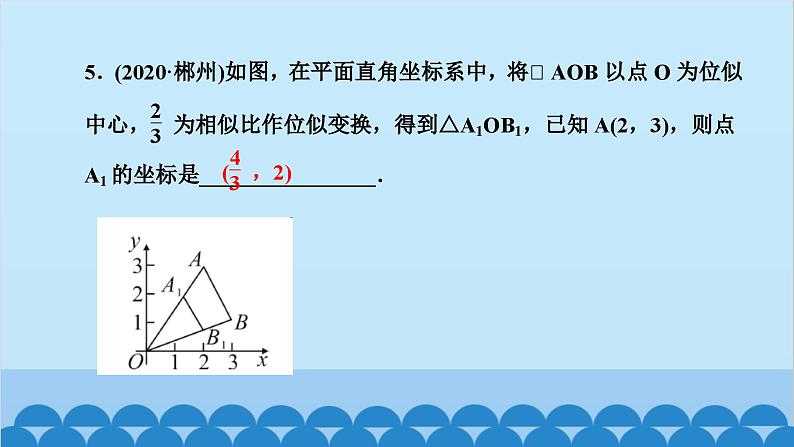








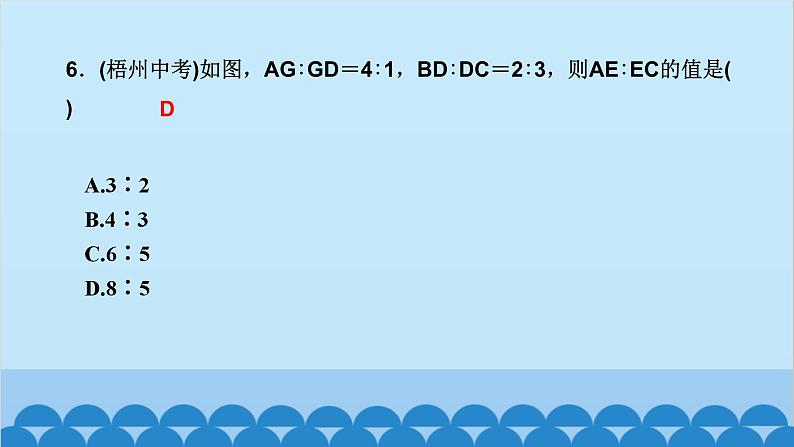


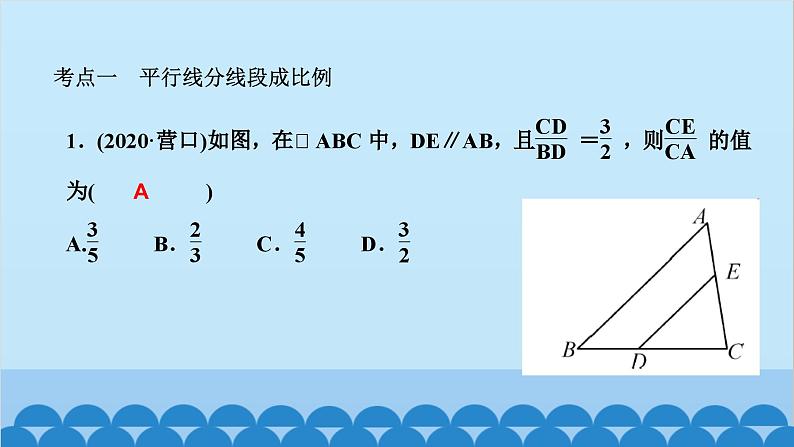
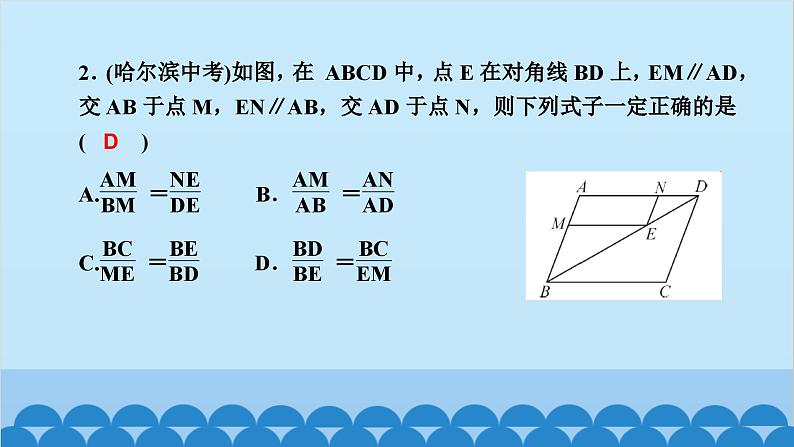
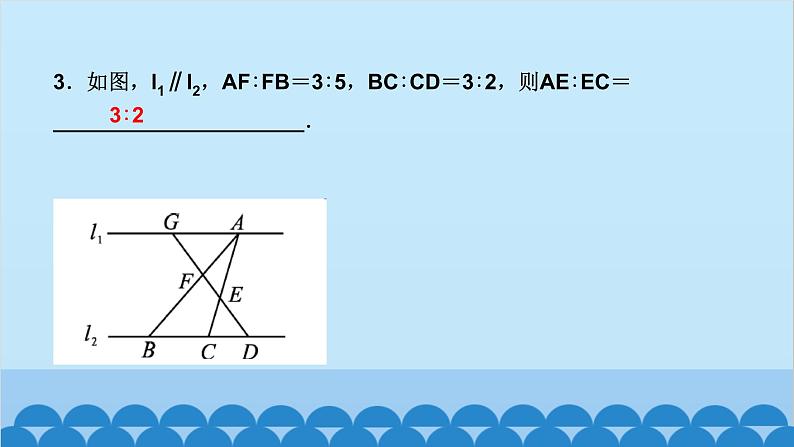
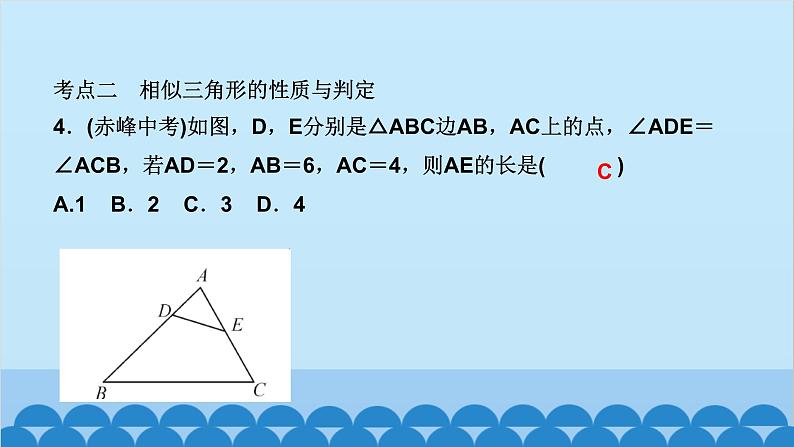
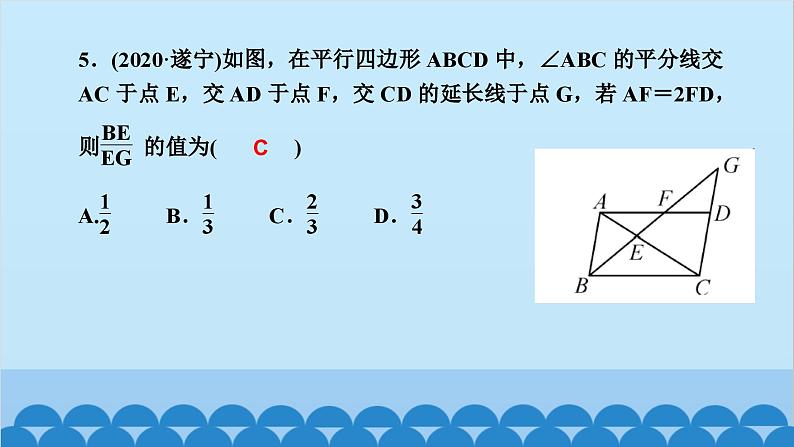
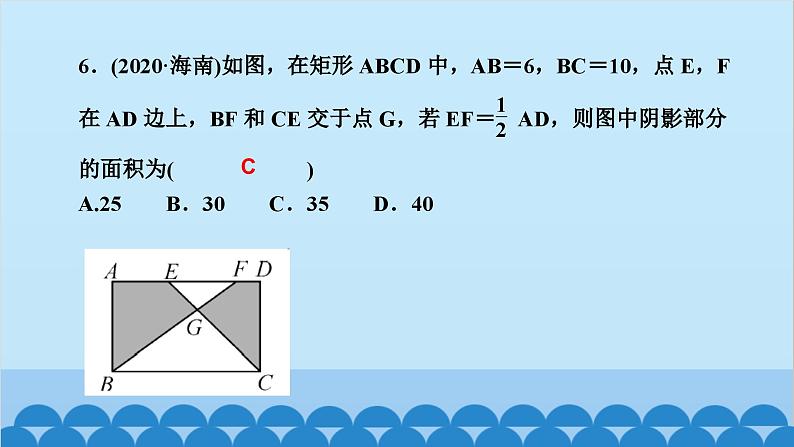
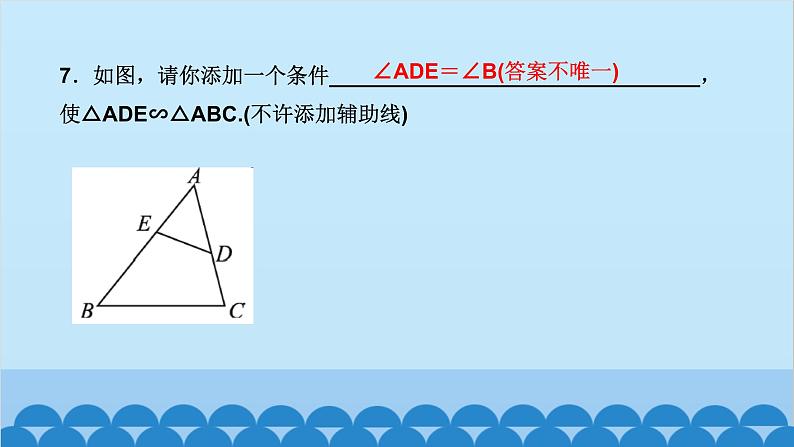
















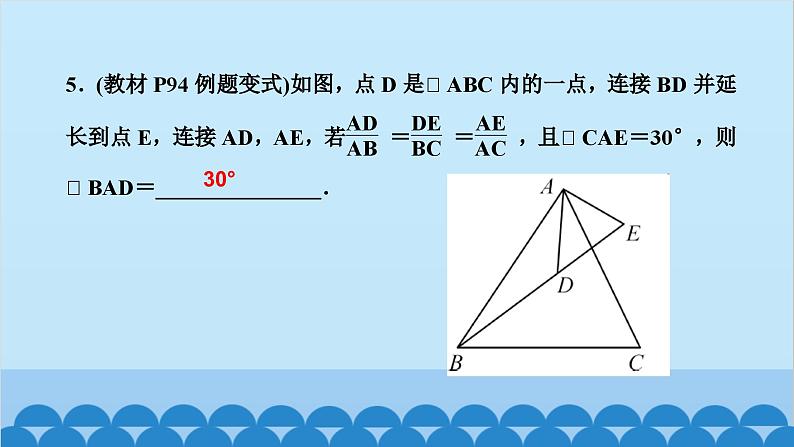


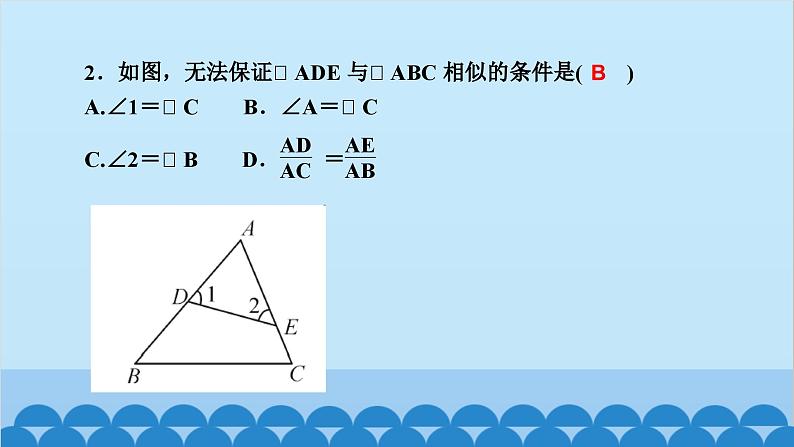
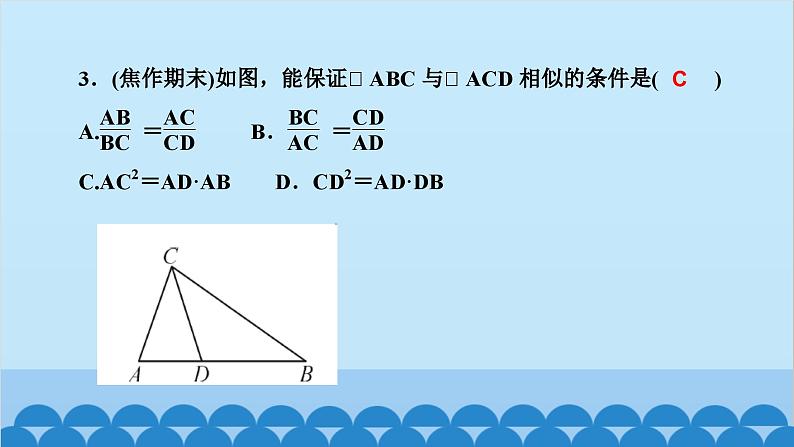

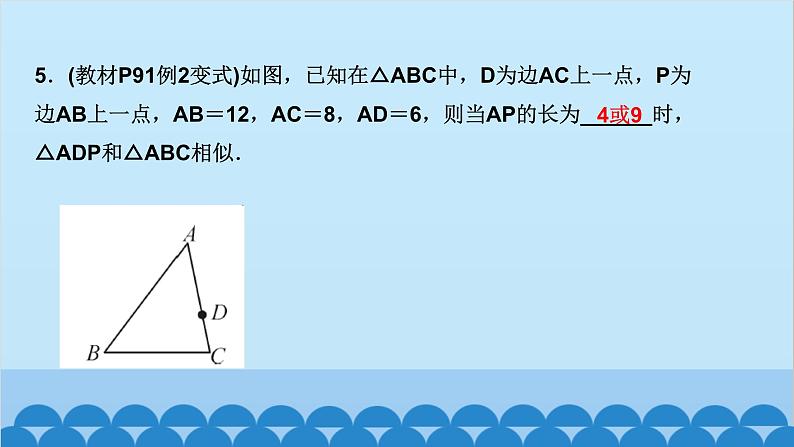
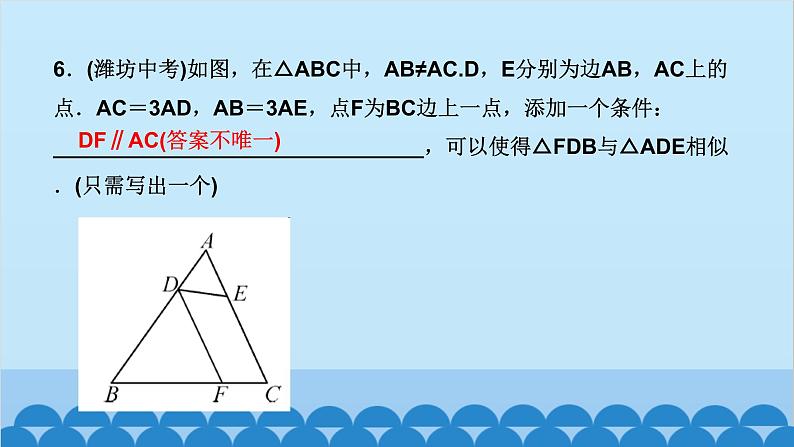

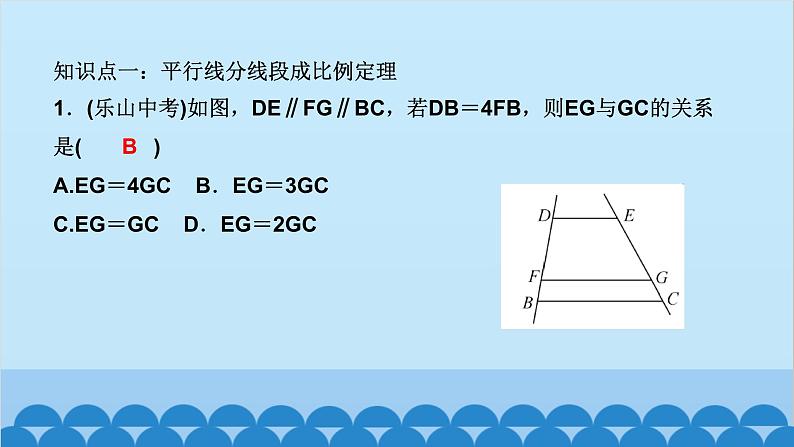
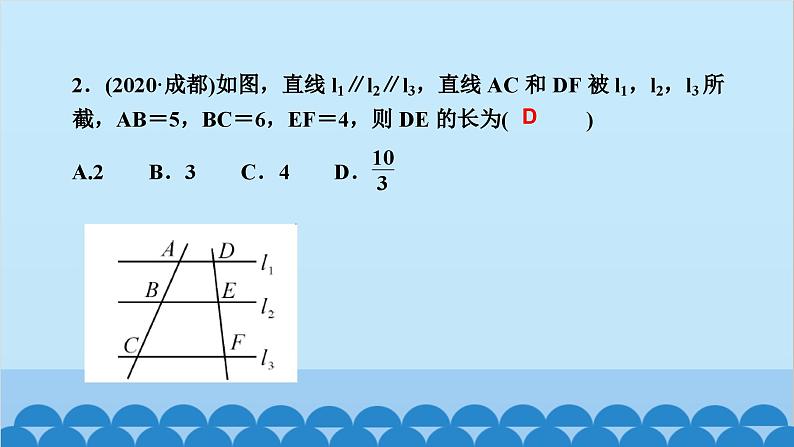
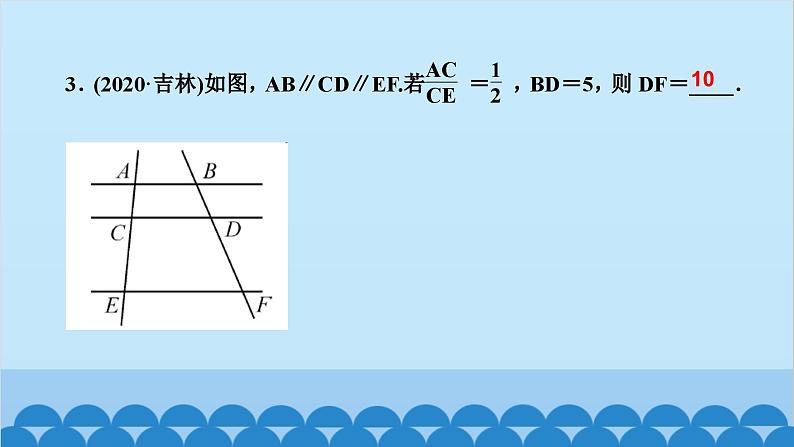
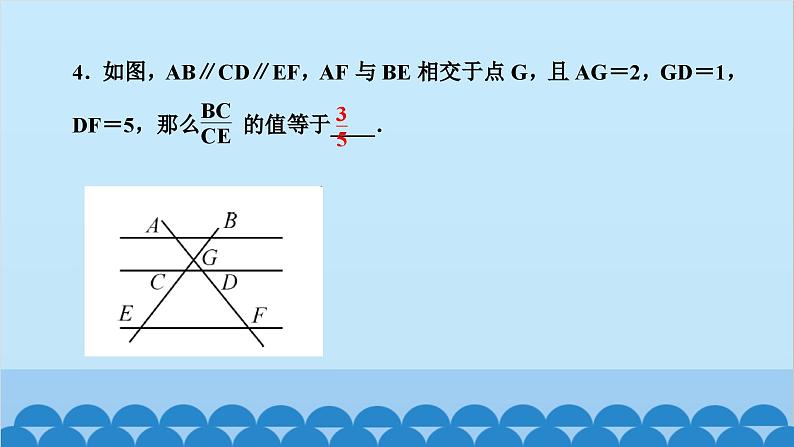
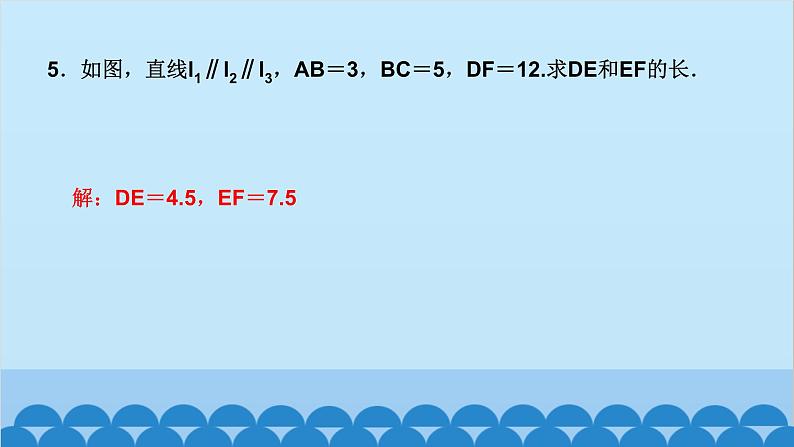
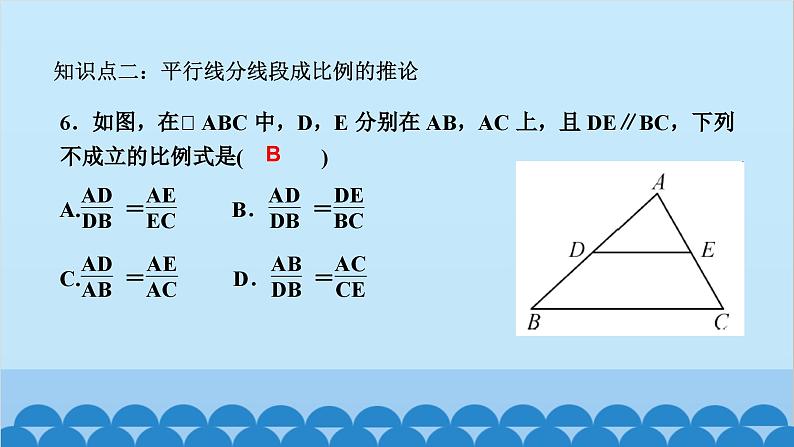
























所属成套资源:北师大版数学九年级上册习题课件
北师大版数学九年级上册 第四章 图形的相似习题课件
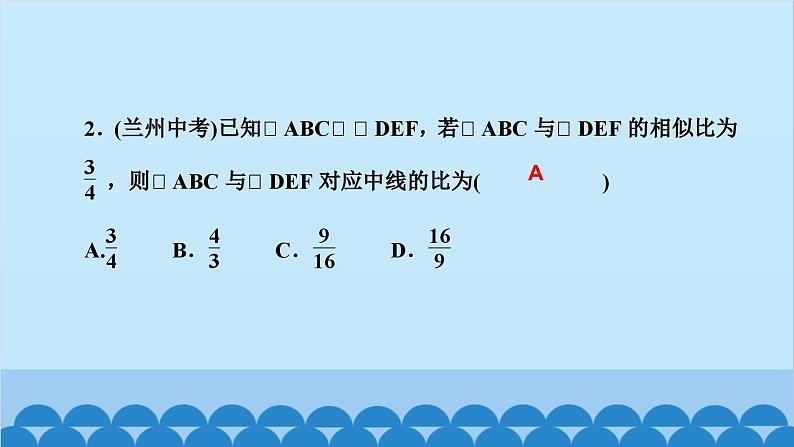
展开
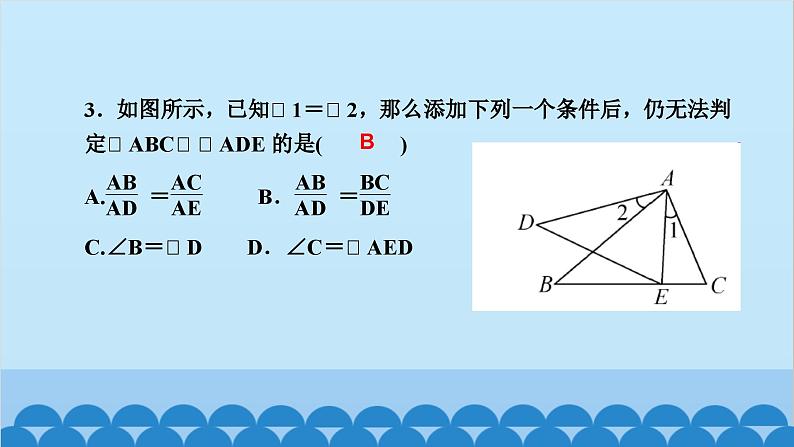
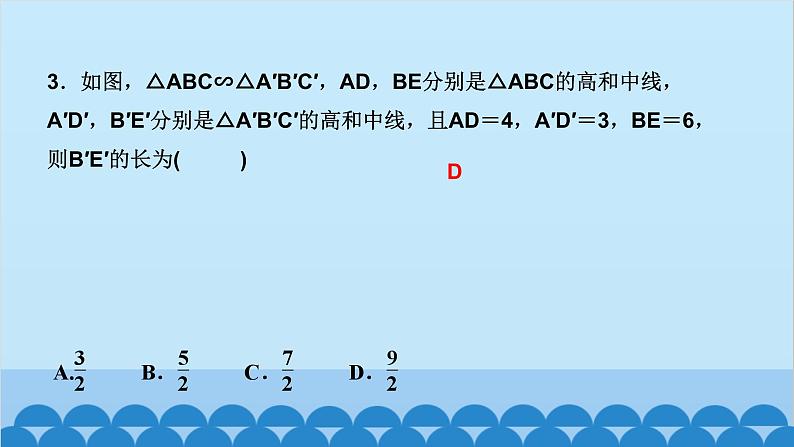
这是一份北师大版数学九年级上册 第四章 图形的相似习题课件,文件包含43相似多边形ppt、阶段自测二ppt、阶段自测三ppt、48第2课时平面直角坐标系中的位似变换ppt、单元复习四图形的相似ppt、48第1课时位似图形及其性质ppt、47第2课时相似三角形的周长与面积的ppt、44第1课时两角分别相等的两个三角形ppt、44第3课时三边成比例的两个三角形相似ppt、专题课堂七相似三角形的基本模型ppt、47第1课时相似三角形中特殊线段的性质ppt、46利用相似三角形测高ppt、44第2课时两边成比例且夹角相等的两ppt、42平行线分线段成比例ppt、45相似三角形判定定理的证明ppt、44第4课时黄金分割ppt、专题课堂八几何类比拓展探究ppt、易错课堂四图形的相似ppt、41第1课时线段的比和比例的基本性质ppt、41第2课时等比的性质ppt等20份课件配套教学资源,其中PPT共263页, 欢迎下载使用。
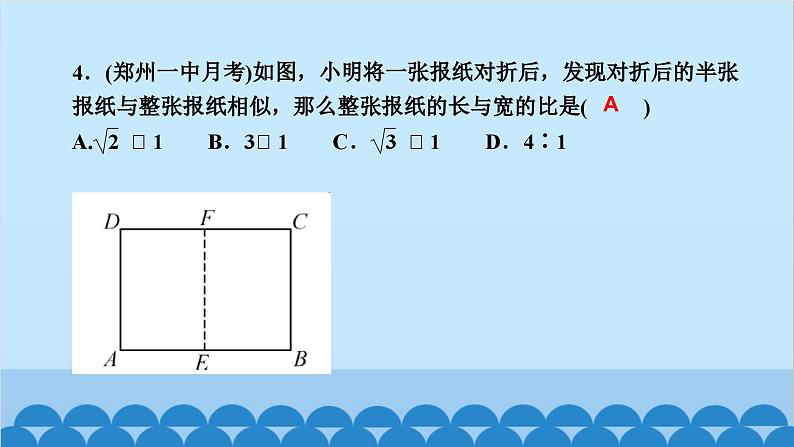
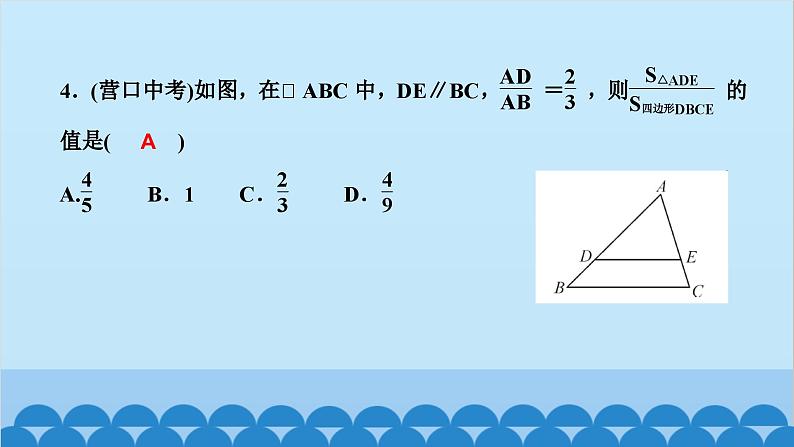
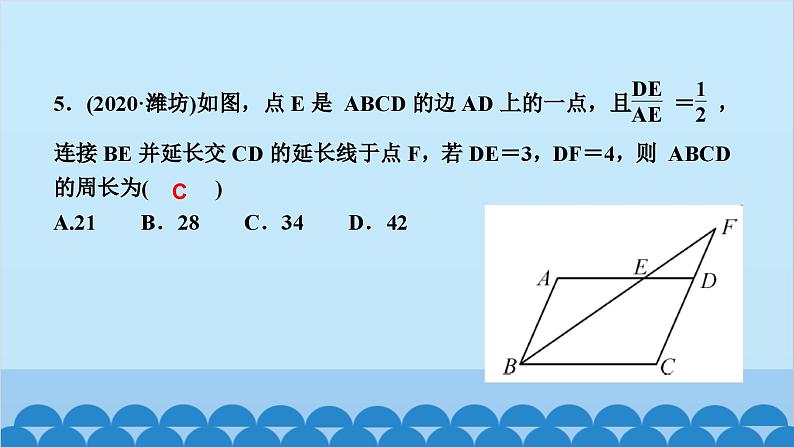
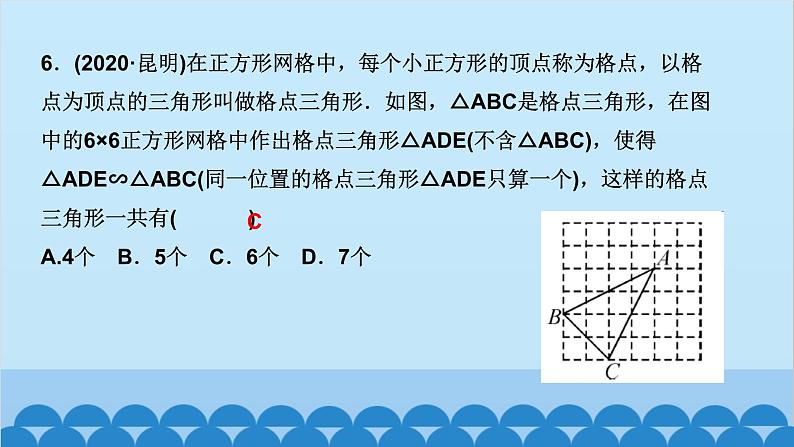
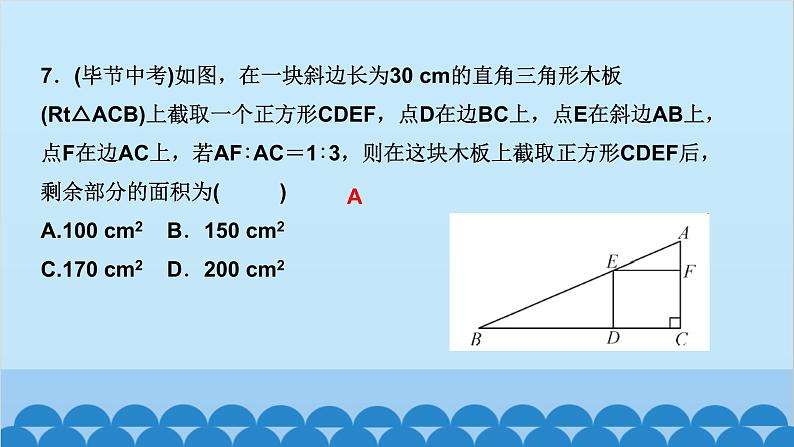
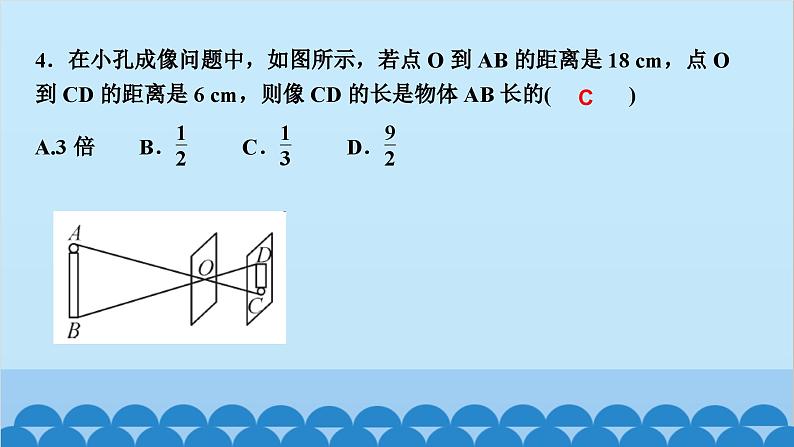
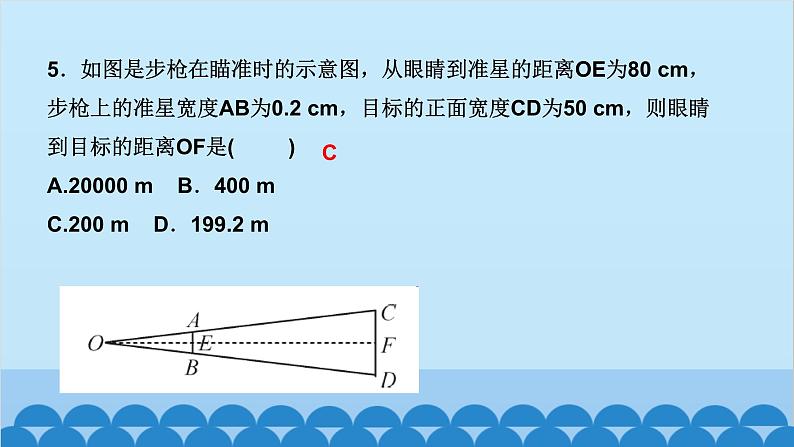
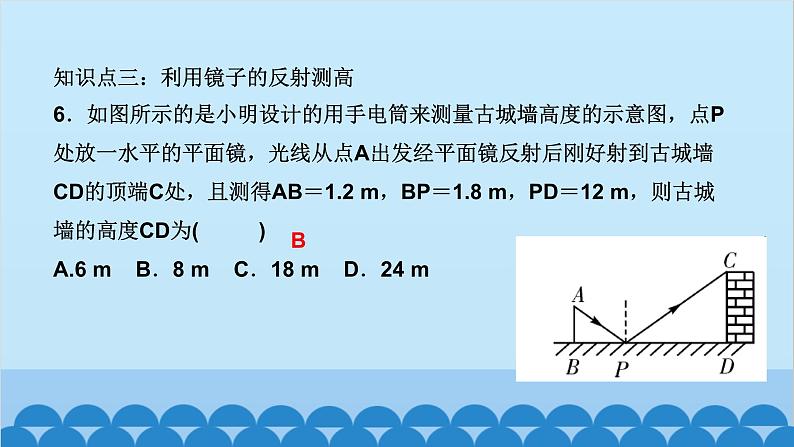
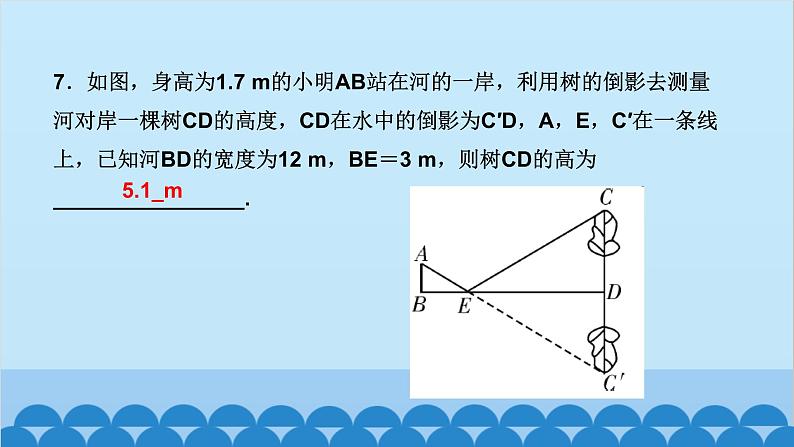
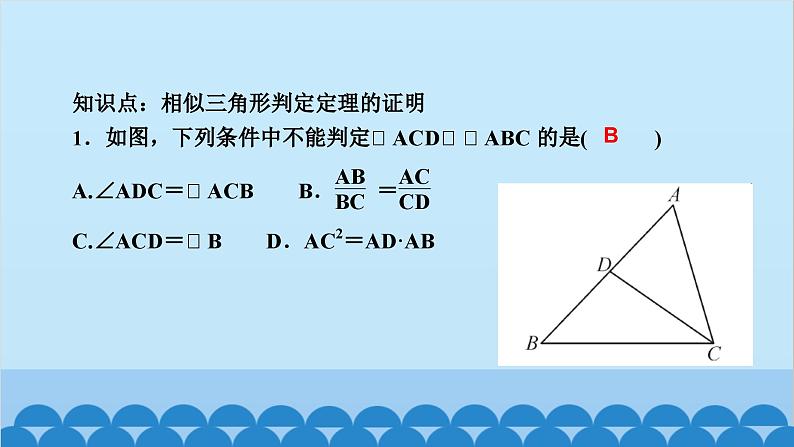
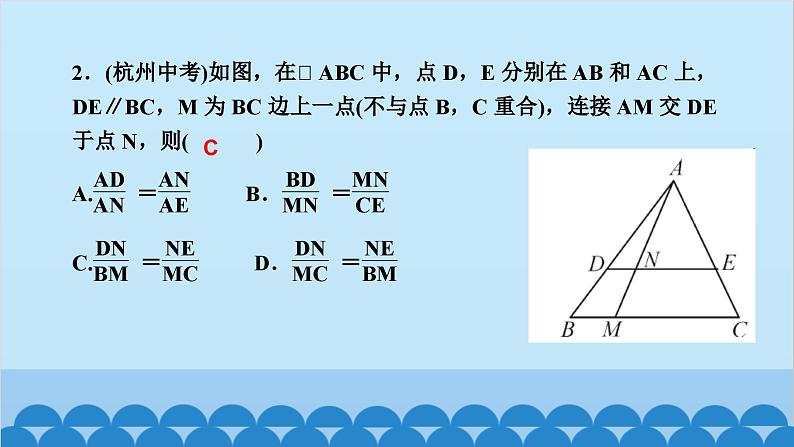
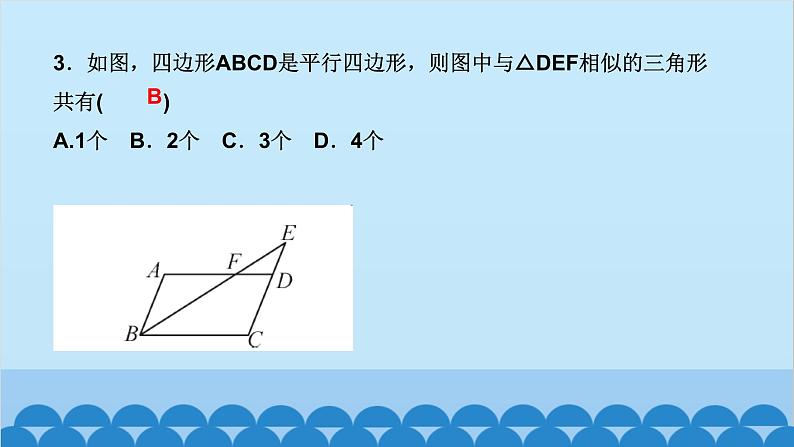
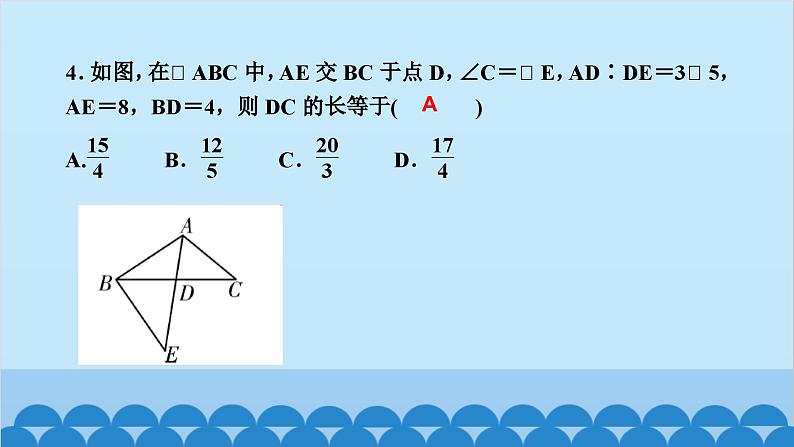
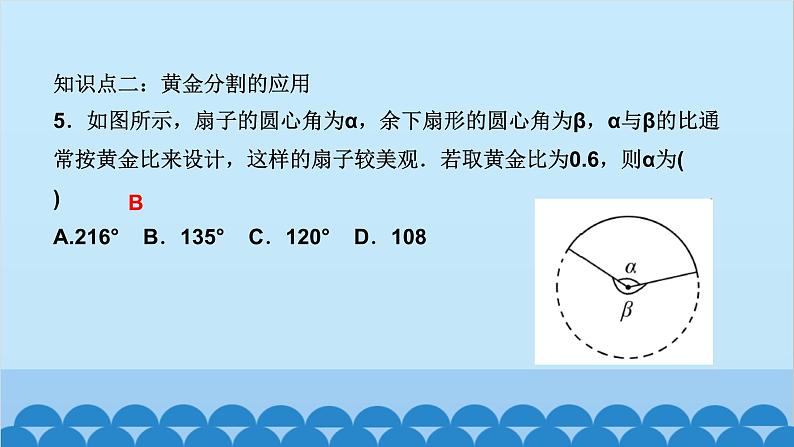
北师版4.6 利用相似三角形测高第四章 图形的相似知识点一:利用阳光下的影子测量高度1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )A.仰角 B.树的影长C.标杆的影长 D.都不需要2.小玲和爸爸正在散步,爸爸身高1.8 m,他在地面上的影长为2.1 m,若小玲比爸爸矮0.3 m,则她的影长为( )A.1.3 m B.1.65 m C.1.75 m D.1.8 mBC3.(驻马店一模)如图,身高为1.8 m的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2 m,BC=18 m,则旗杆CD的高度是____________.18m知识点二:利用标杆测量高度4.(2020·天水)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高是( )A.17.5 m B.17 m C.16.5 m D.18 mA5.(陕西中考)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河的宽AB.知识点三:利用镜子的反射测高6.如图所示的是小明设计的用手电筒来测量古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,且测得AB=1.2 m,BP=1.8 m,PD=12 m,则古城墙的高度CD为( )A.6 m B.8 m C.18 m D.24 mB7.如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条线上,已知河BD的宽度为12 m,BE=3 m,则树CD的高为________________.5.1_m8.如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A,B,C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,求凉亭的高度AB.9.(2020·上海)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为____米.710.(教材P105习题4.10T4变式)阳光通过窗口照射到室内,在地面上留下2.7 m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7 m,窗口高AB=1.8 m,则窗口底边离地面的高BC=____m.411.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2 m,它的影子BC=1.6 m,木杆PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木杆PQ的长度为__________m.2.312.如图,为了测量山的高度,小明在山前的平地上先竖一根已知长度的木棒O′B′,比较木棒的影长A′B′与山的影长AB,即可近似求出山的高度OB.如果O′B′=1 m,A′B′=2 m,AB=270 m,求山的高度.13.(荆门中考)如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2 m,BD=2.1 m,如果小明眼睛距地面髙度BF,DG为1.6 m,试确定楼的高度OE.14.如图,小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB.





