山东省滨州市阳信县2024-2025学年高一上学期期中考试数学试卷(含答案)

这是一份山东省滨州市阳信县2024-2025学年高一上学期期中考试数学试卷(含答案)，共12页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．设集合,,若,则( )
A.2B.1C.D.
2．设a,,则“且”是“”的( )
A.必要不充分条件B.充分不必要条件
C.充分必要条件D.既不充分也不必要条件
3．函数的最小值是( )
A.4B.6C.8D.12
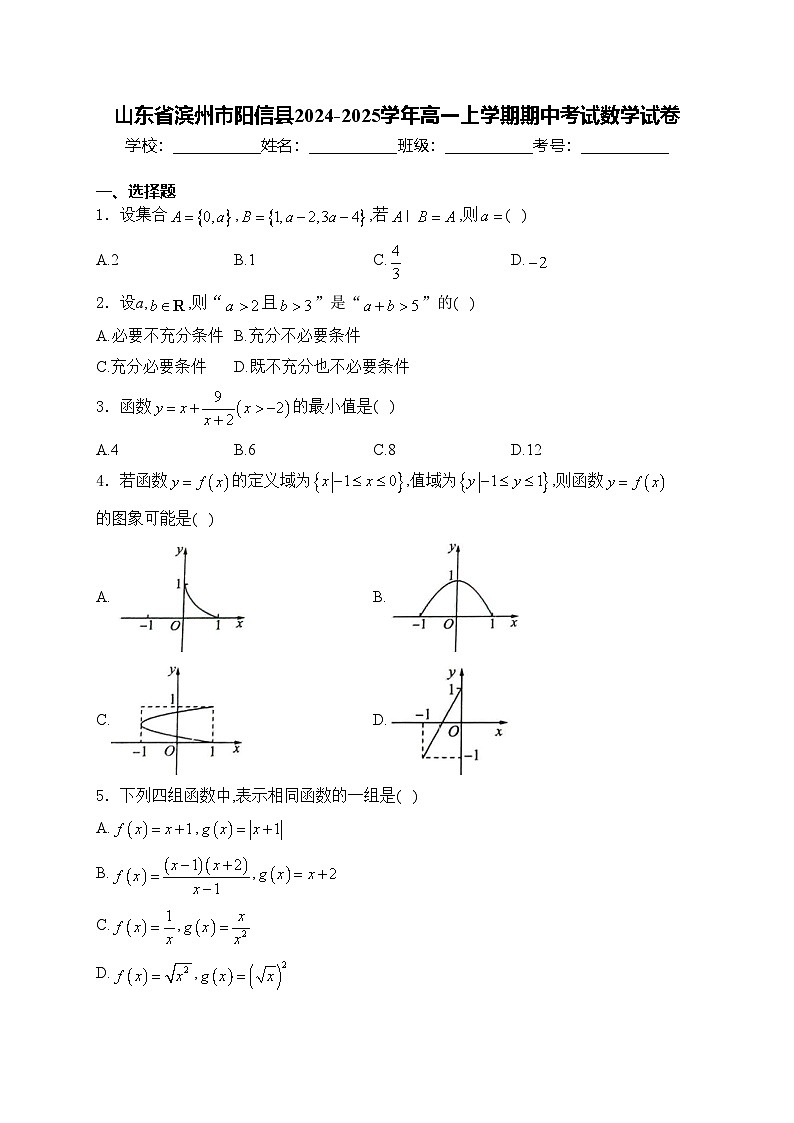
4．若函数的定义域为,值域为,则函数的图象可能是( )
A.B.
C.D.
5．下列四组函数中,表示相同函数的一组是( )
A.,
B.,
C.,
D.,
6．函数的图象经过点,则不等式的解集为( )
A.B.
C.D.
7．下列函数中,既是偶函数,又在区间上单调递减的是( )
A.B.
C.D.
8．下列比较大小中正确的是( )
A.B.
C.D.
二、多项选择题
9．下列说法中错误的有( )
A.命题:,,则命题p的否定是,
B.“”是“”的必要不充分条件
C.命题“,”是真命题
D.“”是“关于x的方程有一正一负根”的充要条件
10．下列命题是假命题的为( )
A.若,则
B.若,则
C.若且,则
D.若且,则
11．已知函数若,则a的值可能为( )
A.B.C.D.
三、填空题
12．设集合,,已知且,则a的取值集合为_________.
13．已知正数x,y满足,则的最小值为_________.
14．如图,某小区要建一座八边形的休闲场所,它的主体造型平面图是由两个周长均为24m的相同的矩形和构成的十字形地域.计划在正方形上建一座花坛,造价为2000元/;在四个相同的矩形（图中阴影部分）内铺上塑胶,造价为100元/;在四个空角（图中四个三角形）内铺上草坪,造价为400元/.若要使总造价不高于24000元,则正方形周长的最小值为_________m.
四、解答题
15．已知集合,.
（1）求,;
（2）若集合,且“,”为假命题,求实数m的取值范围.
16．已知a,b,,关于x的一元二次不等式的解集为.
（1）求b,c的值;
（2）解关于x的不等式.
17．已知函数为上的奇函数,当时,,且.
（1）求函数的解析式;
（2）若实数t满足不等式,求t的取值范围.
18．某物流基地今年初用49万元购进一台大型运输车用于运输.若该基地预计从第1年到第n年花在该台运输车上的维护费用总计为万元,该车每年运输收入为23万元.
（1）该车运输几年开始盈利?（即总收入减去成本及维护费用的差为正值）
（2）若该车运输若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以17万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.
哪一种方案较为合算?请说明理由.
19．已知函数.
（1）当时,求的值域;
（2）若的最小值为,求k的值;
（3）在（2）的条件下,若不等式实数解,求实数a的取值范围.
参考答案
1．答案：A
解析：因为,所以,所以有:若,解得,此时,,符合题意;若,解得,此时,,不符合题意.综上所述,.故选A.
2．答案：B
解析：因为且能推出;不能推出且（如,）,所以“且”是“”的充分不必要条件.故选B.
3．答案：A
解析：因为,所以,所以,当且仅当,即时取等号,所以函数的最小值为4.故选A.
4．答案：D
解析：对A,该函数的定义域为,故A错误;
对B,该函数的定义域为,故B错误;
对C,该图象不为函数图象,故C错误;
对D,该函数的定义域为,值域为,故D正确.故选D.
5．答案：C
解析：对于A,两函数对应关系不同,所以不是相同的函数;
对于B,的定义域为,的定义域为R,定义域不同,所以不是相同的函数;
对于C,的定义域为,的定义域为,定义域相同,对应关系也相同,所以是相同的函数;
对于D,的定义域为R,的定义域为,定义域不同,所以不是相同的函数.故选C.
6．答案：B
解析：由函数的图象经过点,得,则函数在上单调递减,在上单调递减,则在R上单调递减.又,即函数是奇函数,所以不等式,则,即,解得,所以原不等式的解集为.故选B.
7．答案：C
解析：对于A,因为的定义域为,所以函数是非奇非偶函数,故A错误;对于B,根据幂函数的性质可知,在上单调递增,且,设,则,所以是奇函数,故B错误;
对于C,设,则,且,所以是偶函数,且在上单调递减,故C正确;
对于D,显然是偶函数且在上单调递增,故D错误.故选C.
8．答案：C
解析：对于A选项,因为在上单调递增,且,所以,故A错误;
对于B选项,因为在上单调递减,且,所以,故B错误;
对于C选项,为奇函数,且在上单调递增,所以在上单调递增,
因为,且,可得,所以,故C正确;
对于D选项,为偶函数,且在上单调递增,所以,且,所以,故D错误.故选C.
9．答案：ABC
解析：由存在量词命题的否定是全称量词命题,可知命题p的否定是,,故A错误;
由“”不能推出“”,例如,但;由“”也不能推出“”,例如,而,所以“”是“”的既不充分也不必要条件,故B错误;
当时,,故C错误;
关于x的方程有一正一负根,所以“”是“关于x的方程有一正一负根”的充要条件,故D正确.故选ABC.
10．答案：AC
解析：对于A选项,取,,,,则,,所以,故A选项错误;
对于B选项,若,有,则,故B选项正确;
对于C选项,若,则,则,又因为,由不等式的性质可得,故C选项错误;
对于D选项,若且,则,且,所以,D选项正确.故选AC.
11．答案：BD
解析：令,则.当时,由,解得（舍去）或;当时,由,解得,即或5.①当时,若,则,解得（舍去）;若,则,无解;②当时,若,则,解得;若,则,解得（舍去）或.综上,或.故选BD.
12．答案：
解析：因为,即,所以或.若,则或;若,即,则或.由与互异,得,故或.又,即,所以且,解得且.综上所述,a的取值集合为.故答案为.
13．答案：
解析：由得,所以,则,当且仅当,即时,等号成立,所以.又,所以的最小值为.
14．答案：4
解析：设正方形的边长为xm,则正方形的面积为,
四个相同的矩形（即阴影部分）的面积为,
四个空角的面积为.
设总造价为W元,
则.
,即,即,解得,
故正方形周长的最小值为4m.故答案为4.
15．答案：（1）见解析
（2）或
解析：（1）或;
,.
（2）“,”为假命题,
“,”为真命题,即.
又,,
当时,,即,;
当时,由可得,
或
解得.
综上,实数m的取值范围为或.
16．答案：（1）
（2）见解析
解析：（1）因为关于x的一元二次不等式的解集为,
所以关于的一元二次方程的两解为和,
所以解得
（2）由（1）得关于x的不等式,即,
因式分解得.
①当时,原不等式为,解得,即不等式的解集为;
②当时,原不等式为,解得或,所以不等式的解集为;
③当时,原不等式为,解得,即不等式的解集为;
④当时,原不等式为,解得,即不等式的解集为;
⑤当时,原不等式为,解得,即不等式的解集为.
综上可得:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
17．答案：（1）
（2）
解析：（1）因为函数为上的奇函数,且当时,,
所以.
又因为,所以,解得,
所以当时,.
设,则,
所以,
所以.
所以
（2）由（1）知
可得在上是减函数.
又,
所以
解得,
所以t的取值范围是.
18．答案：（1）该车运输3年开始盈利
（2）方案①较为合算
解析：（1）由题意可得,即,
解得,,,
该车运输3年开始盈利.
（2）该车运输若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以17万元的价格卖出,
,
当且仅当时,取等号,
方案①最后的利润为:（万元）;
②当盈利总额达到最大值时,以8万元的价格卖出,盈利总额,
当时,盈利总额达到最大值,
方案②最后的利润为（万元）.
两种方案的利润都是59万元,按照时间成本来看,方案①用时更短,
方案①较为合算.
19．答案：（1）
（2）
（3）
解析：（1）当时,,令,,
则可变换为,.
由二次函数的性质可知,函数在上单调递增,
,
故所求值域为.
（2）函数的最小值为,,
若,则在R上单调递增,没有最小值,不符合题意;
若,可知当时,取得最小值,
即,解得或（舍去）.
综上,.
（3）由题意,有实数解,
即有实数解,可得,
要使此不等式有解,只需即可.
（当且仅当时取等号）,
,
,解得,
即实数a的取值范围为.