安徽省宣城市2024-2025学年九年级上学期11月月考数学试题

这是一份安徽省宣城市2024-2025学年九年级上学期11月月考数学试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
温馨提示：亲爱的同学，你拿到的试卷共七大题，满分150分，时间120分，希望你仔细审题，认真作答，遇到困难时请不要轻易放弃，相信你一定会取得好成绩．
一、选择题（40分）
1．下列函数中属于二次函数的是（ ）
A．B．C．D．
2．下列四组线段中，是成比例线段的是（ ）
A．4cm，3cm，4cm，5cmB．10cm，16cm，5cm，8cm
C．2cm，4cm，6cm，8cmD．9cm，8cm，15cm，10cm
3．如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB＝4，则AD的长为（ ）
第3题图
A．B．C．D．
4．已知抛物线的对称轴在y轴左侧，现将该抛物线先向右平移2个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（ ）
A．－5或1B．5或－1C．1D．5
5．如图是根据某拱桥形状建立的直角坐标系，从中得到函数，在正常水位时水面宽AB＝30m，当水位上升5m时，水面宽CD＝（ ）
第5题图
A．8mB．10mC．15mD．20m
6．在平行四边形ABCD中，则为（ ）
第6题图
A．1:3B．1:4C．1:5D．2:5
7．如图，D，E分别是△ABC的边AC，AB上的点，AE＝1.5，AC＝2，BC＝4，且，则DE的长（ ）
第7题图
A．4B．3C．2D．1
8．矩形OABC中，OA＝1，OC＝2，以O为原点，分别以OA，OC所在直线为x轴和y轴，建立如图所示的直角坐标系，双曲线的图象分别交AB，CB于点E，F，连接OE，OF，EF，，则k＝（ ）
第8题图
A．B．1C．D．
9．一种玻璃水杯的截面如图1所示，其左右轮廓线AC，BD为某一抛物线的一部分，杯口AB＝8cm，杯底CD＝4cm，且AB∥CD，杯深12cm，如图2若盛有部分水的水杯倾斜45°（即∠ABP＝45°），水面正好经过点B，则此时点P到杯口AB的距离为（ ）
第9题图
A．5cmB．6cmC．cmD．7cm
10．在平面直角坐标系中，随着m取值的变化，一次函数y＝2x＋m与函数的图像公共点的个数分别为（ ）
A．0，1，2B．0，1，2，3C．0，1，2，3，4D．1，2，3
二、填空题（20分）
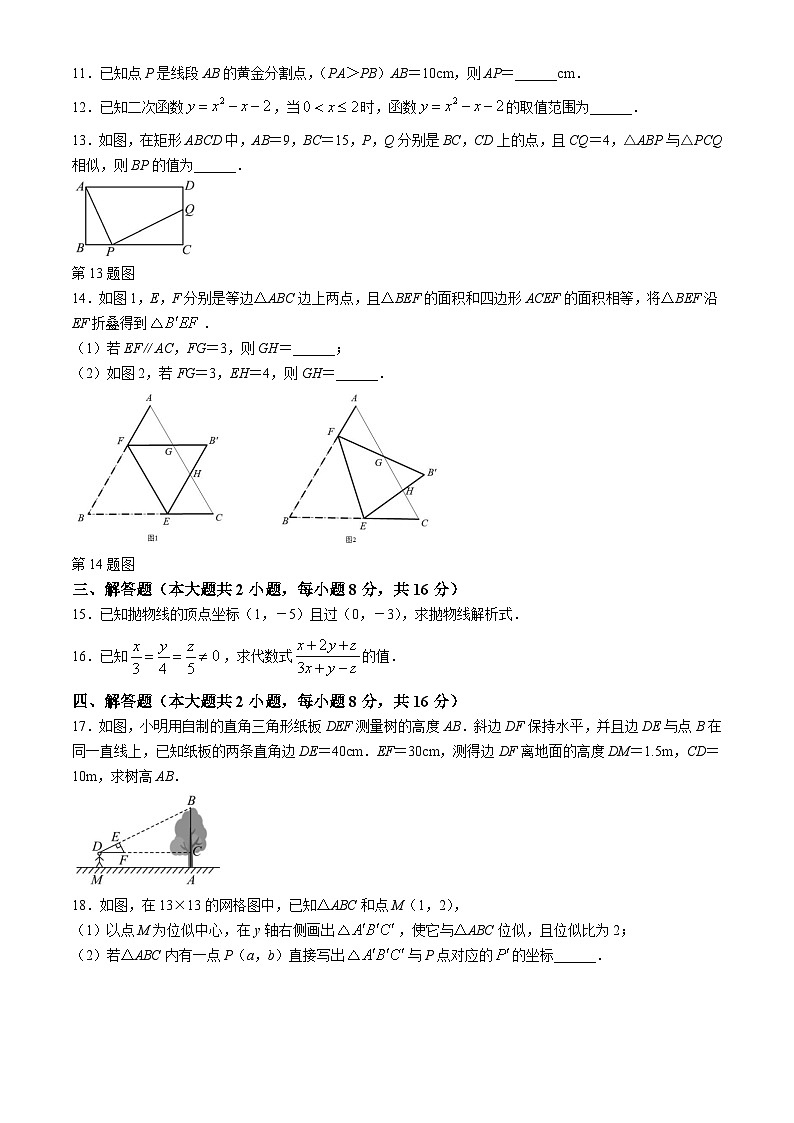
11．已知点P是线段AB的黄金分割点，（PA＞PB）AB＝10cm，则AP＝______cm．
12．已知二次函数，当时，函数的取值范围为______．
13．如图，在矩形ABCD中，AB＝9，BC＝15，P，Q分别是BC，CD上的点，且CQ＝4，△ABP与△PCQ相似，则BP的值为______．
第13题图
14．如图1，E，F分别是等边△ABC边上两点，且△BEF的面积和四边形ACEF的面积相等，将△BEF沿EF折叠得到．
（1）若EF∥AC，FG＝3，则GH＝______；
（2）如图2，若FG＝3，EH＝4，则GH＝______．
第14题图
三、解答题（本大题共2小题，每小题8分，共16分）
15．已知抛物线的顶点坐标（1，－5）且过（0，－3），求抛物线解析式．
16．已知，求代数式的值．
四、解答题（本大题共2小题，每小题8分，共16分）
17．如图，小明用自制的直角三角形纸板DEF测量树的高度AB．斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE＝40cm．EF＝30cm，测得边DF离地面的高度DM＝1.5m，CD＝10m，求树高AB．
18．如图，在13×13的网格图中，已知△ABC和点M（1，2），
（1）以点M为位似中心，在y轴右侧画出，使它与△ABC位似，且位似比为2；
（2）若△ABC内有一点P（a，b）直接写出与P点对应的的坐标______．
五、解答题（本大题共2小题，每小题10分，共20分）
19．某花店在一段时间内推销一种新型花卉，经过统计发现：销售量y（株）与销售时间第x（x为整数）天的变化情况，获得部分数据如表：
（1）请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数关系式；
（2）花店第几天获得的销售量最大？最多销售多少株？
20．如图，AD是直角三角形ABC斜边上的中线，AE⊥AD，AE交CB的延长线于点E．
（1）证明△AEB∽△CEA
（2）若BE＝2，AE＝4，求AB
六、解答题（本大题共2小题，每小题12分，共24分）
21．图1，在Rt△ABC中，∠B＝90°，BC＝4cm．点P以1cm/s的速度从点A出发沿AB匀速运动到B；同时，点Q以vcm/s（v＞1）的速度从点B出发沿BC匀速运动到C．两点同时开始运动，到达各自终点后停止，设运动时间为t（s），△PBQ的面积为S（）．当点Q在BC上运动时，S与t的函数图象如图2所示．
（1）AB＝______cm，v＝______cm/s，补全函数图象；
（2）求出当时间t在什么范围内变化时，△PBQ的面积为S（）的值不小于．
22．设二次函数（b，c是常数）的图像与x轴交于A，B两点．
（1）若A，B两点的坐标分别为（1，0），（2，0），求函数的表达式及其图像的对称轴．
（2）若函数的表达式可以写成（h是常数）的形式，求b＋c的最大值．
（3）设一次函数（m是常数），若函数的表达式还可以写成的形式，当函数的图像经过点时，求的值．
七、解答题（本大题1题，共14分）
23．（1）在△ABC和△DEC中，AB＝AC，DE＝DC，∠BAC＝∠EDC＝90°．
①如图1，当CE与AC重合时，______；
②如图2，△DEC绕点C逆时针旋转一定角度，连接AD，BE，的值是否改变？请说明理由；
（2）如图3，正方形ABCD的边长为2，E为边AB上一动点，以CE为斜边在正方形ABCD内部作等腰直角△CFE，∠CFE＝90°，连接AF，BF，当∠AFE＝∠ABF时，求BE的长．
皖东南四校联考数学试题参考答案
一、选择题（40分）
1．A 2．B 3．A 4．C 5．D 6．B 7．B 8．A 9．D 10．A
二、填空题（20分）
11．cm 12． 13．3或12或
14．（1）（2分） （2）5（3分）
三、解答题
15．设，把（0，－3）代入解析式（2分）
得，解得a＝2（6分）
∴（8分）
16．解：设，（2分）
∴x＝3k，y＝4k，z＝5k，（4分）
∴．（8分）
17．解：依题意，∵∠DMA＝∠MAC＝∠DCA＝90°，∴四边形DMAC是矩形，（2分）
∴AC＝DM＝1.5m
∵∠DEF＝∠BCD＝90°，∠D＝∠D，∴△DEF∽△DCB，（4分）
∴，
∵DE＝40cm＝0.4m，EF＝30cm＝0.3m，CD＝10m，∴，
∴BC＝7.5m，（6分）
∵AC＝DM＝1.5m，
∴AB＝AC＋BC＝1.5＋7.5＝9（m）
∴树高为9m．（8分）
18．（1）解：如图，为所作；
（4分）
（2）（2a－1，2b－2）（8分）
19．（1）解：观察表中数据知，y与x之间的函数关系是二次函数关系，
设，
把（0，0），（1，31），（2，56），代入，得解得，
∴；（4分）
（2）由（1）知，，
∵，∴当时，y取得最大值，
∴在附近取整数，（6分）
当x＝5时，y＝95；当x＝6时，y＝96，
∴花店第6天获得的销售量最大，最多销售96株；（10分）
20．解：（1）∵AD是Rt△BAC斜边中线，∴AD＝CD ∴∠DAC＝∠C
又∵DA⊥AE ∴∠DAE＝∠BAC＝90°
∴∠EAB＝∠DAC＝∠C 又∵∠AEB＝∠CEA
∴△AEB∽△CEA（5分）
（2）∵△AEB∽△CEA ∴ ∵BE＝2AE＝4 ∴
∴EC＝8 BC＝6（8分）
设AB＝a 则AC＝2a 由勾股定理 ∴（10分）
21．（1）解：∵图2是点Q在BC上运动时，S与t的函数图象，
∴当t＝2s时，Q从B点正好运动到C点，
∵BC＝4cm，
∴点Q运动的速度（cm/s），
∵当t＝2s时，，即，
∴（cm），
∵AP＝1×2＝2（cm），∴AB＝AP＋PB＝2＋1＝3（cm）；
当t＞2时，，
当t＝3时，P从A运动到B点，停止，
∴S＝6－2t（2＜t≤3），补全图象如图所示：
故答案为：3；2；补全图象见解析．（6分）
（2）∵当时，AP＝t，BQ＝2t，
∴
，即，
整理得令，解得 由图像可知
解得：，
∵，∴；（9分）
当时，S＝6－2t，
，即，解得：，∴；
综上分析可知，当时，△PBQ的面积为S（）的值不小于．（12分）
22．解：（1）∵二次函数的图象与x轴的交点A、B的坐标分别为（1，0），（2，0），
∴抛物线解析式为，即，
所以抛物线的对称轴为直线；（3分）
（2）∵，
∴，，∴，
∴当h＝1时，b＋c有最大值－1；（8分）
（3）∵ ∴，，
∴，
∴当y＝0时，x－m＝0或x－m－1＝0，
∵函数的图象经过点，
∴时，y＝0，即或，
∴或．
23．解：（1）①∵在△ABC和△DEC中，AB＝AC，DE＝DC，∠BAC＝∠EDC＝90°．
∴在△ABC和△DEC均为等腰直角三角形，，
则△ABC∽△DEC，∴，
故答案为：；（4分）
②不发生变化，理由如下：
∵△ABC和△DEC均为等腰直角三角形，
∴∠ACB＝∠DCE＝45°，，
∵△DEC绕点C逆时针旋转一定角度，如图所示：
∴∠ACB－∠DCB＝∠DCE－∠DCB，∴∠ACD＝∠BCE，
∵，，
∴，∴△ADC∽△BEC，
∴；（9分）
（2）
解法一：连接AC，连接DF 设AE＝x
∵△ADC和△EFC都是等腰直角，
∴△ADC∽△EFC ∠EAC＝∠FDC＝45° ∴
过点F作FG⊥AD交于点G
∵四边形ABCD是正方形，∴∠ADC＝90° 又∵∠FDC＝45°
∴∠FDG＝45°
在Rt△AFG中 即（11分）
又∵∠AFE＝∠ABF ∠BAF＝∠EAF ∴△AFE∽△BAF ∴
解得：或（舍去），BE＝AB－AE＝2－x
∴．（14分）其他解法合理即可．
解法二（2）
连接AC，过F作FP⊥AC垂足为P，设BE＝x，AE＝2－x，
∵四边形ABCD是正方形，∴∠ABC＝90°，AB＝BC＝2，，
∵△CFE是等腰直角三角形，∴，
则，
∵∠AFE＝∠ABF，∠EAF＝∠FAB，∴△EAF∽△FAB，
∴，即，∴，∴，
∵△ABC、△CEF是等腰直角三角形，∴∠ACB＝∠ECF＝45°，
∴∠ACB－∠ACE＝∠ECF－∠ACE，∴∠BCE＝∠PCF，
∵∠EBC＝∠FPC＝90°，∴△EBC∽△FPC，∴，
∵△CEF是等腰直角三角形，∴，
∴，∴，
在Rt△ABC中，AB＝BC＝2，，
∴P是AC的中点，∵FP⊥AC，∴FP垂直平分AC，
∴AF＝CF，∴，解得：或（舍去），
∴．
x
0
1
2
3
4
5
…
y
0
31
56
75
88
95
…