贵州省贵阳市花溪区燕楼中学2024-2025学年九年级上学期11月期中考试数学试题

这是一份贵州省贵阳市花溪区燕楼中学2024-2025学年九年级上学期11月期中考试数学试题，文件包含贵州省贵阳市花溪区燕楼中学2024-2025学年度九年级上学期期中质量监测数学试卷docx、答案pdf等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。

一、选择题(每小题3分，共36分．每小题均有A、B、C、D四个选项，其中只有一个选项正确)
1．下列事件是必然事件的是( )
A．三角形的内角和是180°
B．端午节赛龙舟，红队获得冠军
C．掷一枚质地均匀的骰子，点数是4的一面朝上
D．打开电视，正在播放《新闻联播》
2．下列一元二次方程无实数根的是( )
A．x2＋x－2＝0 B．x2－2x＝0
C．x2＋x＋5＝0 D．x2－2x＋1＝0
3．点P1(－4，y1)，P2(－3，y2)，P3(1，y3)均在二次函数y＝x2＋4x－m的图象上，则y1，y2，y3的大小关系是( )
A．y3>y2>y1 B．y2>y1>y3 C．y1>y2>y3 D．y3>y1>y2
4．同时抛掷两枚质地均匀的正方体骰子1次，下列事件是不可能事件的是( )
A．朝上的点数之和为13 B．朝上的点数之和为12
C．朝上的点数之和为5 D．朝上的点数之和小于5
5．如图可以看成是由一个等腰直角三角形旋转若干次形成的，则每次旋转的度数是( )
A．72° B．60° C．45° D．30°
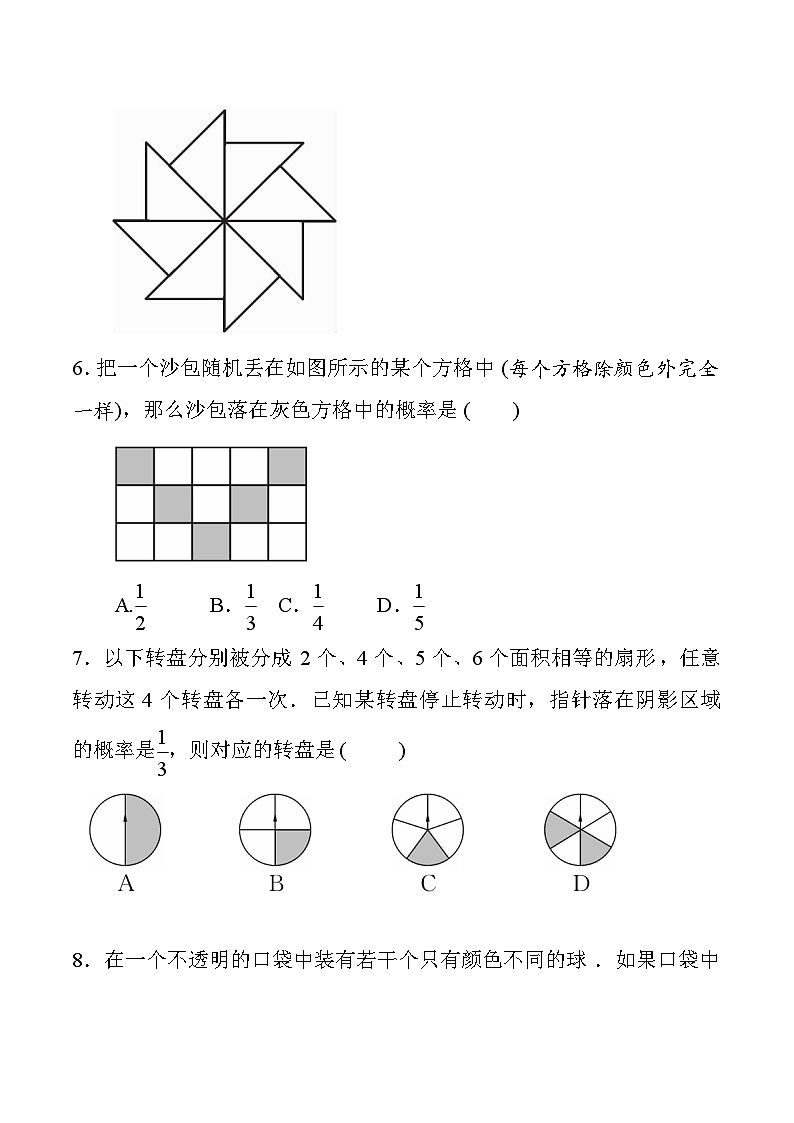
6．把一个沙包随机丢在如图所示的某个方格中(每个方格除颜色外完全一样)，那么沙包落在灰色方格中的概率是( )
A. eq \f(1,2) B． eq \f(1,3) C． eq \f(1,4) D． eq \f(1,5)
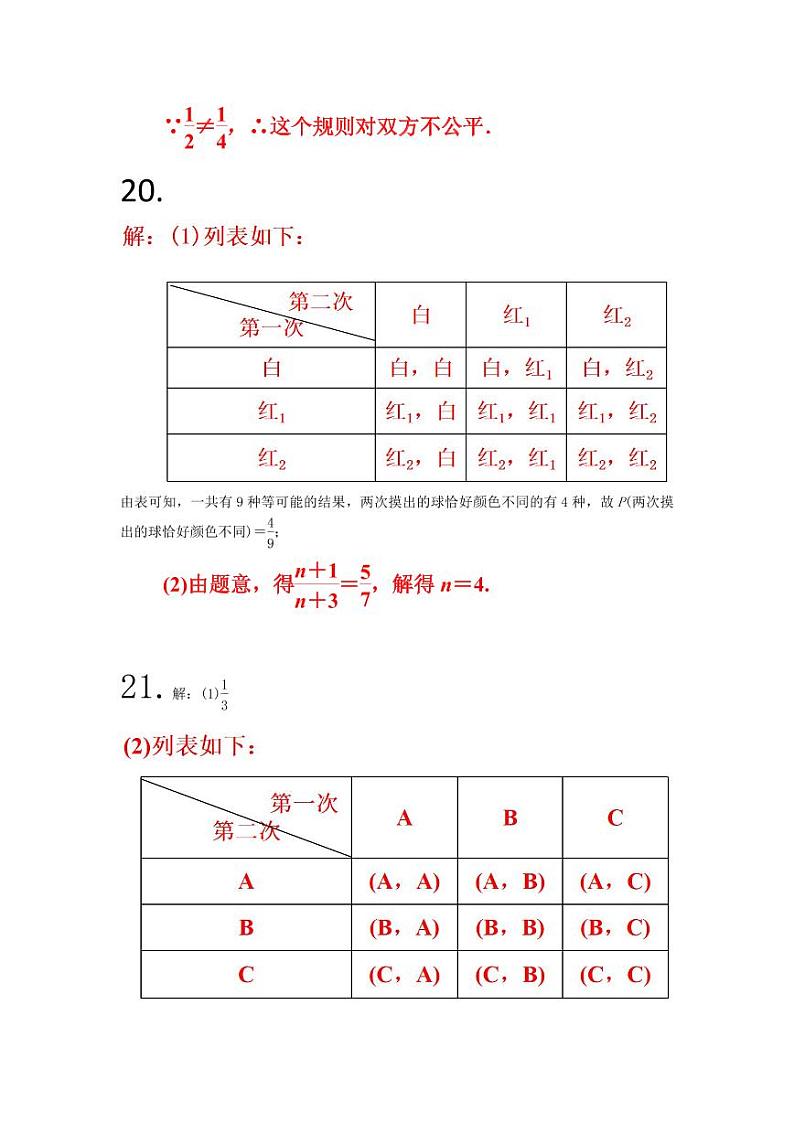
7．以下转盘分别被分成2个、4个、5个、6个面积相等的扇形，任意转动这4个转盘各一次．已知某转盘停止转动时，指针落在阴影区域的概率是 eq \f(1,3)，则对应的转盘是( )
8．在一个不透明的口袋中装有若干个只有颜色不同的球．如果口袋中只装有2个黄球且摸出黄球的概率为 eq \f(1,2)，那么袋中其他颜色的球共有( )
A．1个 B．2个 C．3个 D．4个
9．有六张背面相同的扑克牌，正面上的数字分别是4，5，6，7，8，9.若将这六张牌背面向上洗匀后，从中任意抽取一张，则这张牌正面上的数字是3的倍数的概率为( )
A． eq \f(1,3) B． eq \f(1,2) C． eq \f(1,4) D． eq \f(1,5)
10．某学习小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能的是
A．袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球
B．掷一枚质地均匀的正六面体骰子，向上一面的点数是偶数
C．先后两次掷一枚质地均匀的硬币，两次都出现反面
D．先后两次掷一枚质地均匀的正六面体骰子，两次向上一面的点数之和是7或超过9
11．甲、乙玩转盘游戏时，把质地相同的两个转盘A，B分别平均分成2份和3份，并在每一份内标有数字(如图).游戏规则：甲、乙两人分别同时转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜，数字之和为奇数时乙获胜．若指针落在分界线上，则需要重新转动转盘，则甲获胜的概率是( )
A． eq \f(1,3) B． eq \f(2,3) C． eq \f(5,6) D． eq \f(1,2)
12．投掷一枚质地均匀的骰子两次(骰子的六个面上分别刻有1到6的点数)，向上一面的点数依次记为a，b，那么方程x2＋ax＋b＝0有实数根的概率是( )
A． eq \f(1,2) B． eq \f(1,3) C． eq \f(8,15) D． eq \f(19,36)
二、填空题(每小题4分，共16分)
13．小明用0～9中的数字给手机设置了六位开机密码，但他把最后一位数字忘记了，小明只输入一次密码就能打开手机的概率是____．
14．若圆锥的母线长为10 cm，底面半径为6 cm，则圆锥的侧面积为_______cm2.
15．如图，正六边形ABCDEF内接于⊙O，点P是 eq \(CD,\s\up8(︵))上的任意一点，则∠APB的大小是____．
16．用如图的两个自由转动的转盘做“配紫色”游戏：分别转动两个转盘．若其中一个转出红色，另一个转出蓝色，即可配出紫色，则配成紫色的概率是____．
三、解答题(本大题共8题，共98分．解答应写出必要的文字说明、证明过程或演算步骤)
17．(10分)一个不透明的口袋中放有只有颜色不同的10个球，其中有5个白球、3个黑球、2个红球，以下事件中，哪些是随机事件？哪些是必然事件？哪些是不可能事件？
(1)从口袋中任取1个球是黑球；
(2)从口袋中任取5个球，全是白球；
(3)从口袋中任取6个球，没有白球；
(4)从口袋中任取9个球，白、黑、红三种颜色的球都有；
(5)从口袋中任取1个球，该球是黄色的．
18．(12分)一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球、8个黑球、7个红球．
(1)求从袋中摸出一个球是黄球的概率；
(2)现从袋中取出若干个黑球，搅匀后，使从袋中摸出1个黑球的概率是 eq \f(1,3)，求从袋中取出黑球的个数．
19．(12分)如图是一个转盘，小王和小赵在做游戏，两人各转动这个转盘一次，若指针落在红色上面，则小王得1分；若指针落在白色上面，则小赵得1分；若指针落在黄色上面，双方均不得分，重新再转．问这个规则对双方公平吗？
20．(12分)一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．
(1)摸出1个球，记下颜色后放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率；(要求画树状图或列表)
(2)现再将n个白球放入布袋，搅匀后，使摸出的1个球是白球的概率为 eq \f(5,7)，求n的值．
21．(12分)第19届亚运会于2023年10月8日在杭州结束，有3张分别印有杭州亚运会的吉祥物的卡片：A宸宸、B琮琮、C莲莲．现将这3张卡片(卡片的形状、大小、质地都相同)放在不透明的盒子中，搅匀后从中任意取出一张卡片，记录后放回、搅匀，再从中任意取出一张卡片.
(1)第一次取出的卡片图案为“B琮琮”的概率为________；
(2)用画树状图或列表的方法，求两次取出的2张卡片中至少有1张图案为“A宸宸”的概率．
22．(12分)如图①，一枚质地均匀的正四面体骰子，它有四个面，并分别标有1，2，3，4四个数字．如图②，等边三角形ABC的三个顶点处各有一个圆圈．丫丫和甲甲想玩跳圈游戏，游戏的规则为：游戏者从圈A起跳，每投掷一次骰子，骰子着地的一面点数是几，就沿着三角形的边逆时针方向连续跳跃几个边长．如：若第一次掷得点数为2，就逆时针连续跳2个边长，落到圈C；若第二次掷得点数为4，就从圈C继续逆时针连续跳4个边长，落到圈A.
(1)丫丫随机掷一次骰子，她跳跃后落回到圈A的概率为______；
(2)丫丫和甲甲一起玩跳圈游戏：丫丫随机投掷一次骰子，甲甲随机投掷两次骰子，都以最终落回到圈A为胜者．这个游戏规则公平吗？请说明理由．
23．(14分)一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，4，5，x.甲、乙两人每次同时从袋中各随机摸出一个球，并计算摸出的这2个小球上的数字之和，记录后都将小球放回袋中搅匀，重复进行试验，试验数据如下表．
解答下列问题：
(1)如果试验继续进行下去，根据上表数据，“和为8”出现的频率稳定在它的概率附近，估计“和为8”出现的概率是______；
(2)如果摸出的这两个小球上的数字之和为9的概率是 eq \f(1,3)，那么x的值可以取7吗？请用列表法或画树状图法说明理由；如果x的值不可以取7，请写出一个符合要求的x的值．
24．(14分)为提高学生的安全意识，某学校组织学生参加了“安全知识答题”活动．该校随机抽取部分学生答题成绩进行统计，将成绩分为四个等级：A(优秀)，B(良好)，C(一般)，D(不合格)，并根据结果绘制成如图所示的两幅不完整的统计图．
根据图中所给信息，解答下列问题：
(1)这次抽样调查共抽取________人，条形统计图中的m＝________；
(2)将条形统计图补充完整，在扇形统计图中，求C等级所在扇形圆心角的度数；
(3)该校有1 200名学生，估计该校学生答题成绩为A等级和B等级共有多少人；
(4)学校要从答题成绩为A等级且表达能力较强的甲、乙、丙、丁四名学生中，随机抽出两名学生去做“安全知识宣传员”，请用列表或画树状图的方法，求抽出的两名学生恰好是甲和丁的概率．
摸球总次数
60
90
120
180
240
330
450
“和为8”出现的频数
24
30
37
58
82
110
150
“和为8”出现的频率
0.40
0.33
0.31
0.32
0.34
0.33
0.33