2024年陕西省商洛市山阳县中考数学一模试卷（含解析）

这是一份2024年陕西省商洛市山阳县中考数学一模试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.36的算术平方根为( )
A. ±6B. 6C. −6D. 18
2.如图，a/​/b，c⊥d，∠1=35°，则∠2的度数为( )
A. 55°
B. 65°
C. 75°
D. 85°
3.计算：6x2y3÷(−xy)2=( )
A. 6yB. −6yC. 6xyD. −6xy
4.如图，在△ABC中，点D在BC上，BD=AB，BM⊥AD于点M，N是AC的中点，连结MN，若AB=6，BC=10，则MN为( )
A. 3
B. 4
C. 1
D. 2
5.把函数y=2x−1的图象向上平移3个单位，则下列各点中，在平移后的直线上的点是( )
A. (1,5)B. (2,4)C. (0,3)D. (2,6)
6.如图，在矩形ABCD中，对角线AC，BD交于点O，∠AOB=60°，BC=2 3，则AO的长是( )
A. 4
B. 2
C. 2 3
D. 3
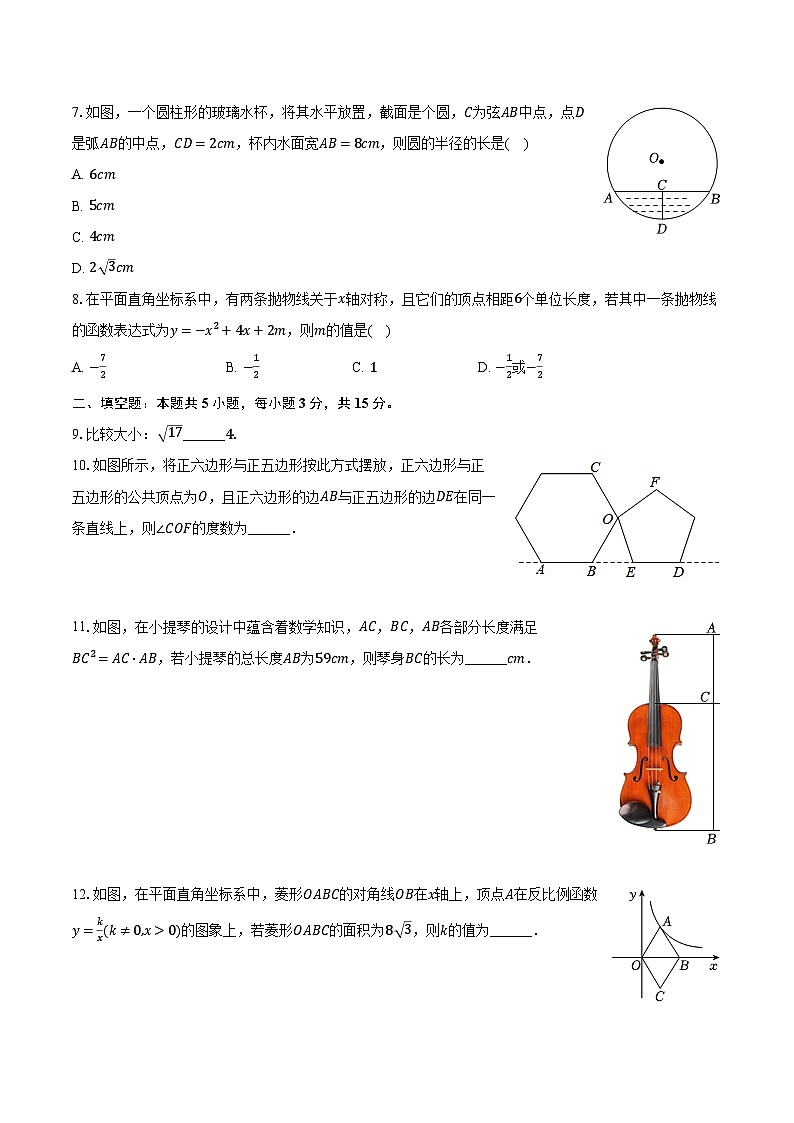
7.如图，一个圆柱形的玻璃水杯，将其水平放置，截面是个圆，C为弦AB中点，点D是弧AB的中点，CD=2cm，杯内水面宽AB=8cm，则圆的半径的长是( )
A. 6cm
B. 5cm
C. 4cm
D. 2 3cm
8.在平面直角坐标系中，有两条抛物线关于x轴对称，且它们的顶点相距6个单位长度，若其中一条抛物线的函数表达式为y=−x2+4x+2m，则m的值是( )
A. −72B. −12C. 1D. −12或−72
二、填空题：本题共5小题，每小题3分，共15分。
9.比较大小： 17______4.
10.如图所示，将正六边形与正五边形按此方式摆放，正六边形与正五边形的公共顶点为O，且正六边形的边AB与正五边形的边DE在同一条直线上，则∠COF的度数为______．
11.如图，在小提琴的设计中蕴含着数学知识，AC，BC，AB各部分长度满足BC2=AC⋅AB，若小提琴的总长度AB为59cm，则琴身BC的长为______cm．
12.如图，在平面直角坐标系中，菱形OABC的对角线OB在x轴上，顶点A在反比例函数y=kx(k≠0,x>0)的图象上，若菱形OABC的面积为8 3，则k的值为______．
13.如图，正方形ABCD的边长为4，点E在线段AD上，以DE为边构造正方形DEFG，使点G在CD的延长线上，连接CF，取CF的中点H，连接DH.当点E在AD边上运动(不含A，D)时，DH的最小值为______．
三、解答题：本题共13小题，共81分。解答应写出文字说明，证明过程或演算步骤。
14.(本小题5分)
计算：(−3)2−6×|−23|+( 3−1)0．
15.(本小题5分)
解不等式组：2x−1≤x,1+xd2．
【解析】(1)根据表中数据得出“门高”，并找到顶点坐标，设出抛物线解析式的顶点式，再用待定系数法求出函数解析式；
(2)令y=0，方别解方程求出方程的解，进而求出d1和d2，从而得出结论．
本题考查二次函数的应用，解题的关键是读懂题意，列出函数关系式．
26.【答案】45° 2
【解析】解：(1)①∵将△ABC绕点A逆时针旋转90°得△ADE，
∴∠EAC=90°，AE=AC，
∴△ACE是等腰直角三角形，
∴∠ACE=45°；
故答案为：45°；
②∵△ACE是等腰直角三角形，
∴CA=CE 2=2 2= 2；
故答案为： 2；
(2)EF=BF+DE，理由如下：
延长CD到K，使DK=BF，如图：
∵∠B=90°，沿边AC翻折得到△ADC，点B的对应点为点D，
∴∠ADC=∠B=90°，AB=AD，
∴∠ADK=90°=∠B，
∵DK=BF，
∴△ADK≌△ABF(SAS)，
∴AK=AF，∠DAK=∠BAF，
∵∠EAF=12∠DAB，
∴∠DAE+∠BAF=∠EAF，
∴∠DAE+∠DAK=∠EAF，即∠EAK=∠EAF，
∵AE=AE，
∴△EAK≌△EAF(SAS)，
∴EF=EK，
∵EK=DK+DE，
∴EF=BF+DE；
(3)将△ADC绕C逆时针旋转至△CBE，连接AE，过点E作EM⊥AB，交AB的延长线于点M，如图：
∴AD=BE，CA=CE，∠ACD=∠ECB，∠ADC=∠EBC，
∴∠ACD+∠ACB=∠ECB+∠ACB，即∠BCD=∠ACE，
∵CDCA=CBCE，
∴△DCB∽△ACE，
∵AC=32CD，
∴BDAE=CDAC=23，
∴BD=23AE，
∵∠BAD+∠BCD=120°，
∴∠ABC+∠ADC=360°−∠BAD−∠BCD=360°−120°=240°，
∵∠ADC=∠EBC，
∴∠ABC+∠EBC=240°，
∴∠ABE=120°，
∴∠EBM=60°，
∵AB=40m，BE=AD=30m，
∴BM=15m，EM= 3BM=15 3m，
∴AM=AB+BM=40+15=55(m)，
∴AE= AM2+EM2= 552+(15 3)2=10 37，
∴BD=23AE=20 373(m)，
∴对角线BD的长为20 373m.
(1)①将△ABC绕点A逆时针旋转90°得△ADE，可得∠EAC=90°，AE=AC，△ACE是等腰直角三角形，故∠ACE=45°；
②由△ACE是等腰直角三角形，可得CA=CE 2= 2；
(2)延长CD到K，使DK=BF，证明△ADK≌△ABF(SAS)，可得AK=AF，∠DAK=∠BAF，而∠EAF=12∠DAB，即可得△EAK≌△EAF(SAS)，EF=EK，从而EK=DK+DE，有EF=BF+DE；
(3)将△ADC绕C逆时针旋转至△CBE，连接AE，过点E作EM⊥AB，交AB的延长线于点M，证明△DCB∽△ACE，可得BDAE=CDAC=23，BD=23AE，由∠BAD+∠BCD=120°，可证∠ABC+∠EBC=240°，即可得∠EBM=60°，根据AB=40m，BE=AD=30m，知BM=15m，EM= 3BM=15 3m，由勾股定理得AE= AM2+EM2=10 37，故BD=23AE=20 373m.
此题是几何变换综合题，主要考查了全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，旋转变换的性质等知识，根据题意作出辅助线，利用三角形全等是解决问题的关键．课题
测量教学楼AB的高度
测量方案示意图
测得数据
CD=4.7m，∠ACG=22°，∠BCG=13°
说明
图上所有点均在同一平面内
参考数据
sin22°≈0.37，cs22°≈0.93，tan22°≈0.40，sin13°≈0.22，cs13°≈0.97，tan13°≈0.23
汽车行驶路程s/km
0
50
100
150
200
…
汽车剩余电量Q/kW⋅h
80
71.5
63
54.5
46
…
水平距离x/m
2
3
6
8
10
12
竖直高度y/m
4
5.4
7.2
6.4
4
0