解析：山东省泰安市新泰市宫里镇初级中学2023-2024学年七年级下学期第一次月考数学试题

这是一份解析：山东省泰安市新泰市宫里镇初级中学2023-2024学年七年级下学期第一次月考数学试题，文件包含精品解析山东省泰安市新泰市宫里镇初级中学2023-2024学年七年级下学期第一次月考数学试题原卷版docx、精品解析山东省泰安市新泰市宫里镇初级中学2023-2024学年七年级下学期第一次月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
(满分150分,时间120分钟)
一、单选题(4'×12=48')
1. 下列方程组中，是二元一次方程组的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题考查了二元一次方程组定义，熟练掌握二元一次方程组的定义是解答本题的关键．根据二元一次方程组的定义判断逐项分析即可，方程的两边都是整式，含有两个未知数，并且未知数的项的次数都是1次的方程叫做二元一次方程．
【详解】解：A．的最高项的次数是2，故不是二元一次方程组；
B．的最高项的次数是2，故不是二元一次方程组；
C．是二元一次方程组；
D．的分母含未知数，故不是二元一次方程组；
故选C．
2. 将式子改写成用含x的式子表示y，正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了解二元一次方程，把x看做已知求出y即可得到答案．
【详解】解：∵，
∴，
故选：B．
3. 若是关于x，y的二元一次方程，则（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】此题主要考查了二元一次方程的定义，关键是掌握二元一次方程需满足三个条件：①首先是整式方程．②方程中共含有两个未知数．③所有未知项的次数都是一次．不符合上述任何一个条件的都不叫二元一次方程．据此进行解答即可．
【详解】解：是关于，的二元一次方程，
，，
解得：．
故选：D．
4. 若方程组的解是，则方程组的解是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了二元一次方程组的解，根据加减法，可得的解，再根据解方程，可得答案，解决本题的关键是先求的解，再求的值．
【详解】解：∵方程组的解是，
∴方程组的解是，
解得，
故选：C．
5. 关于x，y的两个方程组和有相同的解，则的值是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】由题意知，可重新组成两个关于x，y的两个方程组和，先计算不含参的二元一次方程组，得的值，然后代入含参的二元一次方程组，求的值，然后代入求解即可．
【详解】解：∵两个方程组同解
∴可知关于x，y的两个方程组和有相同的解
解方程组
②①得
将代入①式得
解得
∴方程组的解为
将代入方程组得
解关于的方程组
③④得
解得
将代入③式得
解得
∴方程组的解为
∴
故选A．
【点睛】本题考查了同解方程组，解二元一次方程．解题关键在于将两个方程组重新组成新的方程组求解．
6. 小丽家离动物园1200米，其中有一段路为上坡路，另一段路为下坡路．她步行去动物园一共需要20分钟．假设小丽上坡的平均速度是千米时，小丽下坡的平均速度是千米时，若小丽上坡用了小时，下坡用了小时，根据题意可列方程组为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查由实际问题抽象出二元一次方程组，设小丽上坡用了小时，下坡用了小时，根据题意可知：上坡路程下坡路程总路程，上坡时间下坡时间总时间，即可列出相应的方程组，注意单位要统一，解题的关键是明确题意，找出等量关系，列出相应的方程．
【详解】解：设小丽上坡用了小时，下坡用了小时，由题意得，
由米千米，
，
故选：．
7. 在长方形中放入六个长、宽都相同的小长方形，所标尺寸如图所示，则图中阴影部分的面积之和为（ ）
A. 48B. 72C. 36D. 24
【答案】B
【解析】
【分析】本题考查了二元一次方程组的应用，观察图形列出关于x、y的二元一次方程组是解题的关键．设小长方形的长、宽分别为，，根据图示可以列出方程组，然后解方程组即可求出小长方形的面积，接着就可以求出图中阴影部分的面积．
【详解】解：设小长方形的长、宽分别为，
依题意得，
解之得，
∴小长方形的长、宽分别为，
∴
．
故选：B．
8. 如图，为一长条形纸带，，将沿折叠，两点分别与，对应，若，设，根据题意可得（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题主要考查了由实际问题抽象出二元一次方程组，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．
根据翻折的性质可得，由平角的性质列出方程组即可．
【详解】解：根据翻折的性质可得，所以，，
根据题意，得．
故选：D．
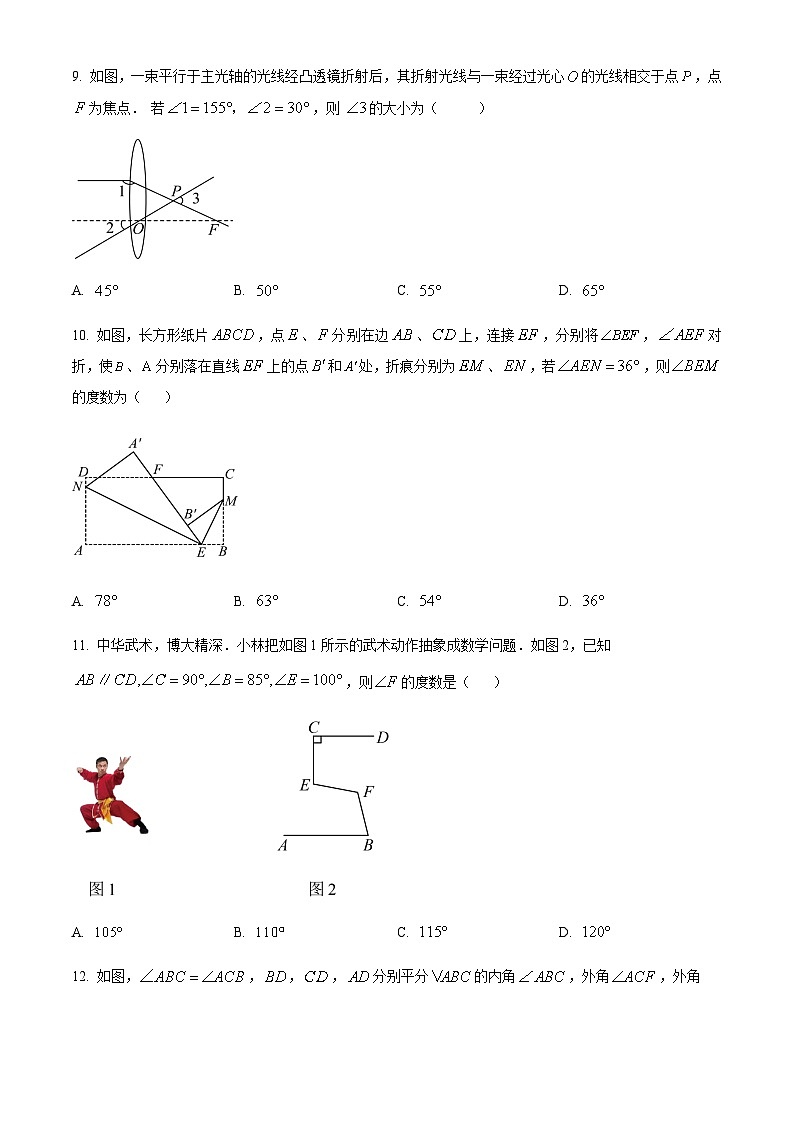
9. 如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心的光线相交于点，点为焦点． 若，则 的大小为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了平行线的性质，三角形外角的性质等知识，掌握这两个知识点是关键．利用平行线的性质及三角形外角的性质即可求解．
[详解】解：如图，
∵，
∴，
∴，
∵，
∴，
故选：C．
10. 如图，长方形纸片，点、分别在边、上，连接，分别将，对折，使、分别落在直线上的点和处，折痕分别为、，若，则的度数为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】此题主要考查了图形的折叠变换及性质，设，由折叠的性质得：，，则，，再由平角的定义得，则，由此解出即可得出的度数．
【详解】解：设，
由折叠的性质得：，，
，，
，
，
解得：，
．
故选：C．
11. 中华武术，博大精深．小林把如图1所示的武术动作抽象成数学问题．如图2，已知，则的度数是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查平行线的性质，解题的关键是作出辅助线．过点E，F分别作的平行线，由平行线的性质得到，分别求出，即可求解．
【详解】解：过点E，F分别作的平行线，
，
，
，
，
，
，
，
故选：A．
12. 如图，，，，分别平分的内角，外角，外角．以下结论：；；；；．其中正确的结论有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
【分析】根据角平分线的定义得出，，，，根据三角形的内角和定理得出，，根据三角形外角性质得出，，根据已知结论逐步推理，即可判断各项．
【详解】解：平分，
，
，，
，
，
，故正确；
，
，
平分，，
，故正确；
，
，
，
，
，
，
，
，故正确；
平分，
，
，
，
，
平分，
，
，，
，
，
，
，故正确；
由得，，
，
，
，故正确；
故选：D．
【点睛】本题考查了三角形外角的性质、角平分线的定义、平行线的性质、三角形内角和定理的应用，主要考查学生的推理能力，有一定难度．
二、填空题(4'×6=24')
13. 一次函数的图象和的图象相交于点，则关于的二元一次方程组的解为 __．
【答案】
【解析】
【分析】本题主要考查一次函数与二元一次方程组的运用，掌握一次函数的交点与二元一次方程组的解的运用是解题的关键．
根据一次函数的交点，把点代入一次函数，可解出的值，由此即可求解．
【详解】解：∵一次函数的图象和的图象相交于点，
∴，
解得，
∴，
∴二元一次方程组的解为，
故答案为：．
14. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等．如图所示是一个未完成的幻方，则__________．
【答案】6
【解析】
【分析】本题考查了二元一次方程的应用以及数学常识，找准等量关系，正确列出二元一次方程是解题的关键．根据每一横行、每一竖列以及两条对角线上的3个数之和相等，可列出关于，的二元一次方程，变形后，即可得出结论．
【详解】解：根据题意得：，
．
故答案为：6．
15. 关于，的二元一次方程组的解满足，则满足条件的值为_______．
【答案】
【解析】
【分析】本题考查了二元一次方程组的解和解二元一次方程组，将，得出，再根据方程组的解满足列出方程并解答即可．能选择适当的方法求解是解此题的关键．
【详解】解：
，得
∵关于，的二元一次方程组的解满足，
解得：
故答案为：．
16. 如图，中，于点，交于点，平分，平分，则的度数是______．
【答案】##135度
【解析】
【分析】本题考查角平分线的定义和三角形内角和定理，设，得出，，进而即可求解
【详解】解：设，
∵，
∴，
∵平分，
∴，
∴，
∵，
∴，
∵平分，
∴，
∴，
故答案为：
17. 如图，，，，则______．
【答案】
【解析】
【分析】本题考查了平行线的性质，三角形内角和定理，由平行线的性质可得，根据，可得，再由三角形内角和定理即可求出，掌握平行线的性质是解题的关键．
【详解】解：∵，
∴，
∵，
∴，
∵，
∴，
∴，
故答案为：．
18. 如图，，，且，，则的度数为______°．

【答案】
【解析】
【分析】设，，根据三角形内角和公式可求得，，推得，根据三角形内角和公式可求得，将代入即可求解．
【详解】解：设，，如图：

∵，，
在中，，
在中，，
又∵，
∴，
故，
在中，，
在中，，
，
将代入可得；
故答案为：．
【点睛】本题考查了三角形内角和定理，熟练掌握三角形内角和定理是解题的关键．
三、解答题(共78分)
19. 解下列方程组：
（1）
（2）
（3）
（4）
【答案】（1）
（2）
（3）
（4）
【解析】
【分析】本题主要考查了解二元一次方程组：
（1）利用加减消元法解方程即可；
（2）利用加减消元法解方程即可；
（3）利用加减消元法解方程即可；
（4）利用加减消元法解方程即可．
【小问1详解】
解：
得：，解得，
把代入①得：，解得，
∴方程组的解为；
[小问2详解】
解：
得：，解得，
把代入②得：，解得，
∴方程组的解为；
【小问3详解】
解：
整理得，
得：，解得，
把代入①得：，解得，
∴方程组解为；
【小问4详解】
解：
整理得，
得：，解得，
把代入①得：，解得，
∴方程组的解为．
20. 甲、乙两人解关于的方程组，甲因看错，解得，乙将其中一个方程的写成了它的相反数，解得，求的值．
【答案】
【解析】
【分析】本题考查了二元一次方程组的解的定义，将代入得：，即可得出的值，将代入得：，即可得出的值，从而得解．
【详解】解：将代入得：，
解得：，
乙将其中一个方程的写成了它的相反数，解得，
将代入得：，
解得：，
综上所述：．
21. 某企业积极落实二十大精神，争取通过增收减支，到今年年底使企业利润翻一番，该企业的具体目标是：保证今年总产值比去年增加20%，总支出比去年减少20%，已知该企业去年的利润（利润总产值总支出）为200万元，求今年的总产值，总支出分别是多少万元？
【答案】总产值，总支出分别是720万元和320万元
【解析】
【分析】设去年的总产值，总支出分别是x万元和y万元，根据题意列二元一次方程组解题即可．
【详解】解：设去年的总产值，总支出分别是x万元和y万元，
则，
解得：，
∴今年的总产值为：万元，
总支出为万元，
答：今年的总产值，总支出分别是720万元和320万元．
【点睛】本题考查二元一次方程组的应用，找准等量列方程组是解题的关键．
22. 某商场上周购进年冬奥会吉祥物冰墩墩与冬残奥会吉祥物雪容融两种毛绒玩具共个，共花去元，这两种吉祥物毛绒玩具的进价、售价如下表：
（1）求冰墩墩、雪容融这两种毛绒玩具分别购进了多少个？
（2）上周五售出这两种吉祥物毛绒玩具，共获得利元．那么这一天售出的冰墩墩、雪容融这两种毛绒玩具分别是多少个？
【答案】（1）购进冰墩墩毛绒玩具个，雪容融毛绒玩具个
（2）售出冰墩墩毛绒玩具个，雪容融毛绒玩具个或售出冰墩墩毛绒玩具个，雪容融毛绒玩具个
【解析】
【分析】（1）设购进冰墩墩毛绒玩具个，雪容融毛绒玩具个，根据数量关系列方程即可求解；
（2）由（1）可知毛绒玩具的价格，设售出冰墩墩毛绒玩具个，雪容融毛绒玩具个，由此列方程即可求解．
【小问1详解】
解：设购进冰墩墩毛绒玩具个，雪容融毛绒玩具个，
依题意得：，解得：．
∴购进冰墩墩毛绒玩具个，雪容融毛绒玩具个．
【小问2详解】
解：设售出冰墩墩毛绒玩具个，雪容融毛绒玩具个，
依题意得：，
∴．
又∵，均为正整数，
∴或．
∴售出冰墩墩毛绒玩具个，雪容融毛绒玩具个或售出冰墩墩毛绒玩具个，雪容融毛绒玩具个．
【点睛】本题主要考查二元一次方程组与销售问题的综合，理解题意中的数量关系列方程是解题的关键．
23. 如图，，，，．
（1）求证：；
（2）若平分，求的度数．
【答案】（1）见解析；
（2）见解析．
【解析】
【分析】本题考查了垂直定义、平行线的性质和判定以及角平分线的定义．
（1）由垂直定义证明，再由，证明，进而得到；
（2）由得到，从而得到，再由平分得到，则的度数可求．
【小问1详解】
证明：∵，，
∴，
∴，
∵，
∴,
∴
【小问2详解】
∵，
∴，
∵，
∴，
∵平分，
∴，
∵，
∴．
24. 如图，直线、交于点，，分别平分和，且．
（1）求证：；
（2）若，求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】本题考查了平行线的判定，根据题目的已知条件并结合图形进行分析是解题的关键．
（1）先利用角平分线的定义可得，，从而利用平角定义可得，然后利用同角的余角相等可得，再利用平行线的判定可得，即可解答；
（2）利用（1）的结论可得，然后利用平角定义可得，，然后利用对顶角相等可得，再利用角平分线的定义可得，从而利用平角定义进行计算即可解答．
【小问1详解】
证明：，分别平分和，
，，
，
，
，
，
；
【小问2详解】
解：，，
，
，
，，
，
平分，
，
，
的度数为．
25. 中，是的角平分线，是的高．
（1）如图1，若，，求的度数；
（2）如图2，，由的计算结果，你能发现与的数量关系吗？写出这个关系式，并加以证明；
（3）如图3，，延长到点，和的角平分线交于点、请直接写出的度数______．
【答案】（1）
（2）
（3）
【解析】
【分析】（1）根据三角形的内角和定理可求得，由角平分线的定义可得的度数，利用三角形的高线可求得度数，进而求解即可得出结论；
（2）根据（1）的推理方法可求解、、的数量关系；
（3）由三角形外角的性质结合角平分线的定义可求解，根据三角形内角和定理即可求解．
【小问1详解】
，，，
，
是的角平分线，
，
是的高，
，
，
，
；
【小问2详解】
，
，
是的角平分线，
，
是的高，
，
，
，
即；
【小问3详解】
∵，
∴
∴
∵是的角平分线，
∴
∴
是的角平分线，
∴
∵是的角平分线
∴
中，，
故答案为：．
【点睛】本题主要考查角平分线的定义，三角形外角的性质，三角形的内角和定理，三角形的高线，角平分线等知识的综合运用，掌握以上基础知识是解本题的关键．
进价（元/个）
售价（元/个）
冰墩墩
雪容融