备战2025年高考数学精品教案第十章计数原理、概率、随机变量及其分布第4讲随机事件与概率（Word版附解析）

这是一份备战2025年高考数学精品教案第十章计数原理、概率、随机变量及其分布第4讲随机事件与概率（Word版附解析），共17页。
学生用书P232
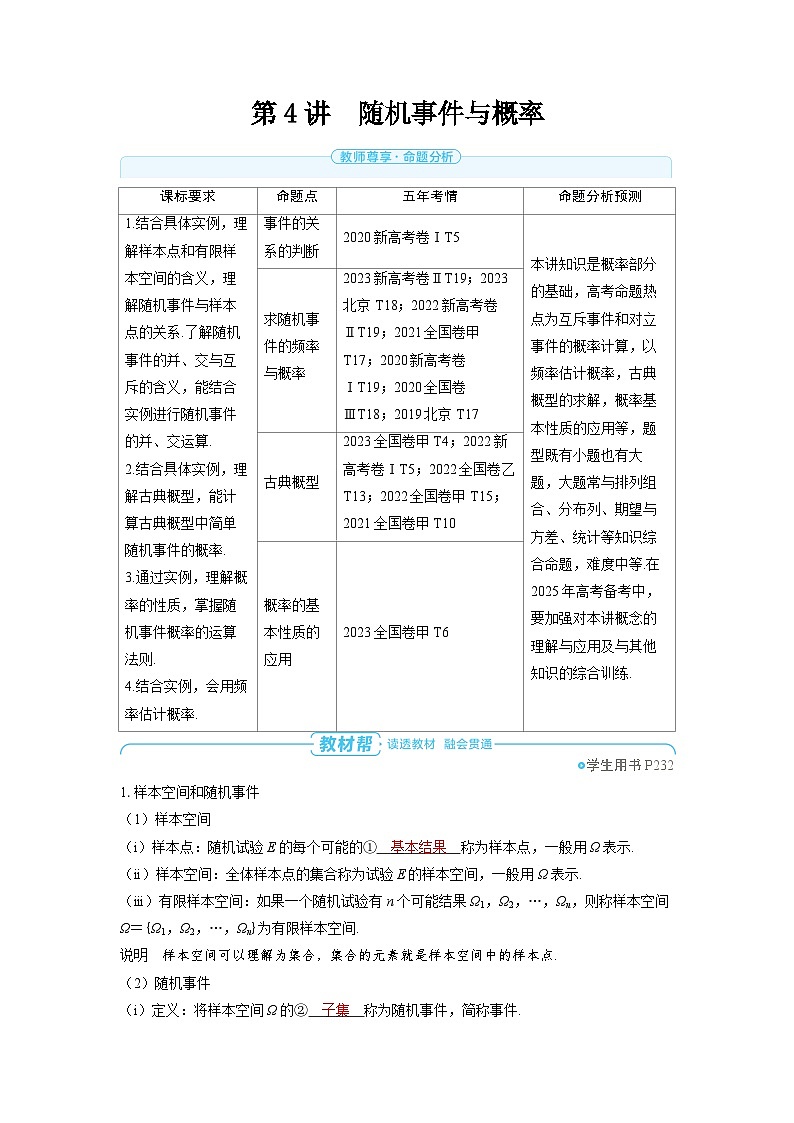
1.样本空间和随机事件
（1）样本空间
（i）样本点：随机试验E的每个可能的① 基本结果 称为样本点，一般用Ω表示.
（ii）样本空间：全体样本点的集合称为试验E的样本空间，一般用Ω表示.
（iii）有限样本空间：如果一个随机试验有n个可能结果Ω1，Ω2，…，Ωn，则称样本空间Ω＝{Ω1，Ω2，…，Ωn}为有限样本空间.
说明 样本空间可以理解为集合，集合的元素就是样本空间中的样本点.
（2）随机事件
（i）定义：将样本空间Ω的② 子集 称为随机事件，简称事件.
（ii）表示：一般用大写字母A，B，C，…表示.
（iii）极端情形：③ 必然事件 、不可能事件.
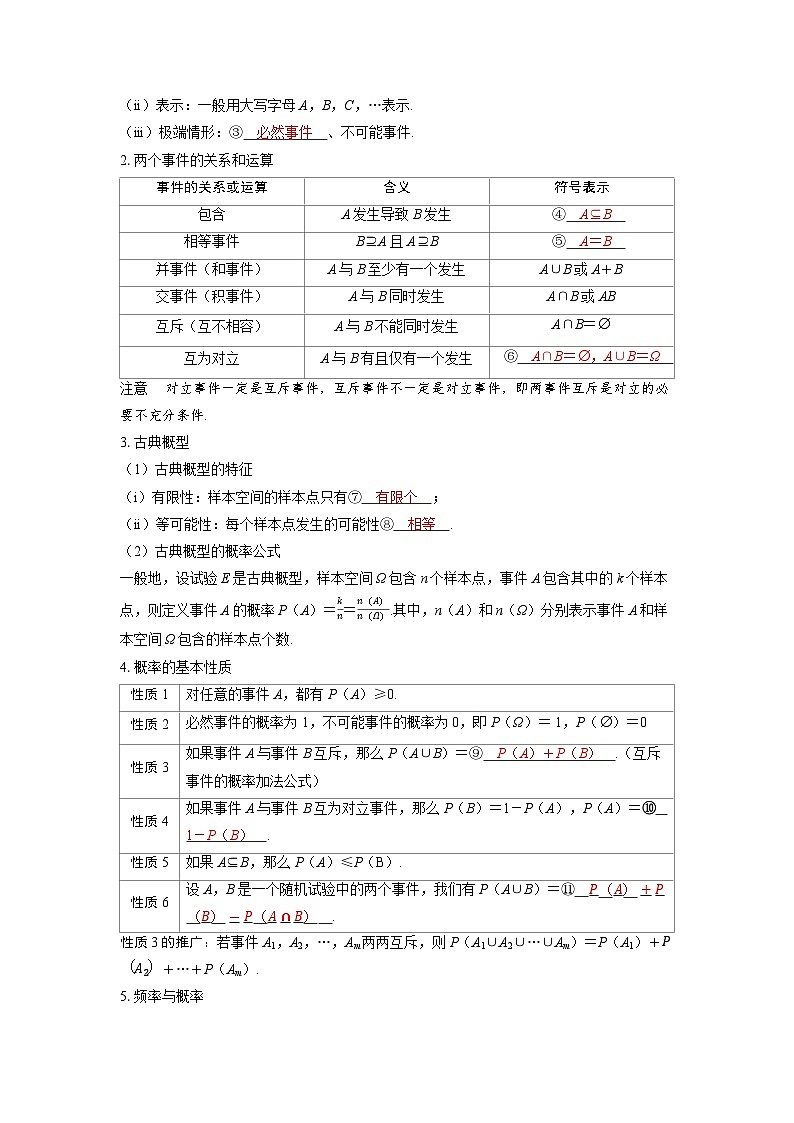
2.两个事件的关系和运算
注意 对立事件一定是互斥事件，互斥事件不一定是对立事件，即两事件互斥是对立的必要不充分条件.
3.古典概型
（1）古典概型的特征
（i）有限性：样本空间的样本点只有⑦ 有限个 ；
（ii）等可能性：每个样本点发生的可能性⑧ 相等 .
（2）古典概型的概率公式
一般地，设试验E是古典概型，样本空间Ω包含n个样本点，事件A包含其中的k个样本点，则定义事件A的概率P（A）＝kn＝n（A）n（Ω）.其中，n（A）和n（Ω）分别表示事件A和样本空间Ω包含的样本点个数.
4.概率的基本性质
性质3的推广：若事件A1，A2，…，Am两两互斥，则P（A1∪A2∪…∪Am）＝P（A1）＋PA2＋…＋P（Am）.
5.频率与概率
（1）频率的稳定性
一般地，随着试验次数n的增大，频率偏离概率的幅度会缩小，即事件A发生的频率fn（A）会逐渐稳定于事件A发生的概率P（A）.我们称频率的这个性质为频率的稳定性.
（2）频率稳定性的作用：可以用频率fn（A）估计概率P（A）.
说明 随机事件A发生的频率是随机的，而概率是客观存在的确定的常数，但在大量随机试验中，事件A发生的频率稳定于事件A发生的概率.
1.一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（ D ）
A.至多有一次中靶B.两次都中靶
C.只有一次中靶D.两次都不中靶
解析 射击两次的结果有：一次中靶，两次中靶，两次都不中靶，故至少有一次中靶的互斥事件是两次都不中靶.故选D.
2.[教材改编]下列说法错误的是（ D ）
A.任一事件的概率总在[0，1]内B.不可能事件的概率为0
C.必然事件的概率为1D.概率是随机的，在试验前不能确定
解析 任一事件的概率总在[0，1]内，不可能事件的概率为0，必然事件的概率为1，概率是客观存在的，是一个确定值.
3.[教材改编]若随机事件A，B互斥，A，B发生的概率均不等于0，且P（A）＝2－a，PB=4a-5，则实数a的取值范围是（ D ）
A.（54，2）B.（54，32）C.[54，32]D.（54，43]
解析 由题意可知0