备战2025年高考数学精品教案第八章平面解析几何第2讲两条直线的位置关系（Word版附解析）

这是一份备战2025年高考数学精品教案第八章平面解析几何第2讲两条直线的位置关系（Word版附解析），共13页。
学生用书P172
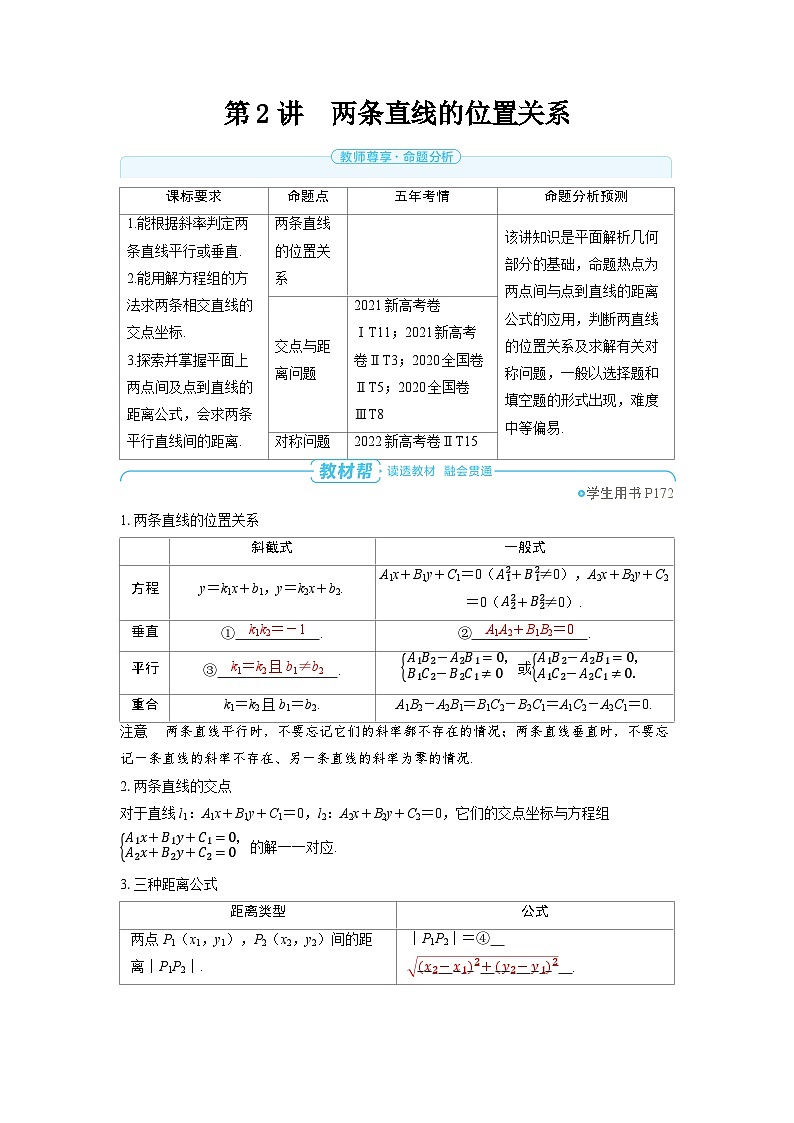
1.两条直线的位置关系
注意 两条直线平行时，不要忘记它们的斜率都不存在的情况；两条直线垂直时，不要忘记一条直线的斜率不存在、另一条直线的斜率为零的情况.
2.两条直线的交点
对于直线l1：A1x＋B1y＋C1＝0，l2：A2x＋B2y＋C2＝0，它们的交点坐标与方程组A1x＋B1y＋C1=0，A2x＋B2y＋C2=0的解一一对应.
3.三种距离公式
注意 点到直线、两平行线间的距离公式的使用条件：（1）求点到直线的距离时，应先将直线方程化为一般式；（2）求两平行线间的距离时，应先将方程化为一般式且x，y的系数对应相等.
1.下列说法正确的是（ A ）
A.若两直线的方程组成的方程组有解，则两直线不一定相交
B.点P（x0，y0）到直线y＝kx＋b的距离为｜kx0＋b｜1+k2
C.当直线l1和直线l2的斜率都存在时，一定有k1＝k2⇒l1∥l2
D.若两条直线垂直，则他们的斜率之积一定等于－1
2.设直线l1：y＝k1x＋1，l2：y＝k2x－1，其中实数k1，k2满足k1k2＋2＝0，则l1与l2的位置关系是（ B ）
A.平行B.相交C.重合D.不确定
解析 假设l1与l2平行或重合，有k1＝k2，代入k1k2＋2＝0，得k12＋2＝0，与k1为实数的事实相矛盾，从而k1≠k2，即l1与l2相交.故选B.
3.已知直线l1：3x－y－1＝0，l2：x＋2y－5＝0，l3：x－ay－3＝0不能围成三角形，则实数a的取值不可能为（ A ）
A.1B.13C.－2D.－1
解析 由题意可得，若三条直线不能围成三角形，则其中有两条直线平行或三条直线经过同一点.若其中有两条直线平行，当l1∥l3时，可得a＝13，当l2∥l3时，可得a＝－2；若三条直线经过同一点，由3x－y=1，x+2y=5，可得直线l1与l2的交点为（1，2），则（1，2）在l3上，故可得1－2a－3＝0，解得a＝－1.综上，实数a的值可能为13，－2，－1.故选A.
4.[易错题]直线2x＋2y＋1＝0与x＋y＋2＝0之间的距离是 324 .
解析 先将2x＋2y＋1＝0化为x＋y＋12＝0，则两平行线间的距离d＝｜2－12｜2＝324 .（注意应用公式时x，y的系数分别对应相等）
5.[教材改编]已知点A（2，1），B（3，4），C（－2，－1），则△ABC的面积为 5 .
解析 解法一 设AB边上的高为h，则h就是点C到AB所在直线的距离.
｜AB｜＝（3－2）2＋（4－1）2＝10.由两点式可得AB边所在直线的方程为y－14－1＝x－23－2，即3x－y－5＝0.点C（－2，－1）到直线3x－y－5＝0的距离h＝|3×-2--1-5|32+-12＝10，所以S△ABC＝12×｜AB｜×h＝12×10×10＝5.
解法二 易知AB＝（1，3），AC＝（－4，－2），
所以△ABC的面积为12×｜1×（－2）－3×（－4）｜＝5.（二级结论：若AB＝（x，y），AC＝（u，v），则S△ABC＝12｜xv－yu｜）
学生用书P173
命题点1 两条直线的位置关系
例1 （1） [2023四川凉山州二模]已知直线l1：mx－y＋1＝0，直线l2：4x－my＋2＝0，若l1∥l2，则m＝ －2 .
解析 因为l1∥l2，所以－m2＝－4，2m≠4，（注意排除直线重合情况）
解得m＝－2.
（2）经过点A（2，1）且与直线2x＋y－10＝0垂直的直线方程为 x－2y＝0 .
解析 因为所求直线与直线2x＋y－10＝0垂直，所以设该直线方程为x－2y＋c＝0，又直线过点A（2，1），所以有2－2×1＋c＝0，解得c＝0，故所求直线方程为x－2y＝0.
方法技巧
1.判断两条直线位置关系的注意点
（1）斜率不存在的特殊情况；
（2）可直接利用直线方程系数间的关系得结论.
2.与直线Ax＋By＋C1＝0垂直的直线系方程为Bx－Ay＋C2＝0，与直线Ax＋By＋C1＝0平行的直线系方程为Ax＋By＋C2＝0（C1≠C2），过直线l1：A1x＋B1y＋C1＝0和l2：A2x＋B2y＋C2＝0的交点的直线系方程为A1x＋B1y＋C1＋λ（A2x＋B2y＋C2）＝0（λ∈R）（该直线系不含l2）.
训练1 （1）[2023南昌市模拟]直线l1：ax＋（a＋1）y－1＝0，l2：（a＋1）x－2y＋3＝0，则“a＝2”是“l1⊥l2”的（ A ）
A.充分不必要条件 B.必要不充分条件
C.充要条件D.既不充分也不必要条件
解析 若l1⊥l2，则a（a＋1）＋（a＋1）×（－2）＝0，解得a＝－1或a＝2，所以“a＝2”是“l1⊥l2”的充分不必要条件，故选A.
（2）过点A（1，－4）且与直线2x＋3y＋5＝0平行的直线方程为 2x＋3y＋10＝0 .
解析 设所求直线方程为2x＋3y＋c＝0（c≠5），由题意知，2×1＋3×（－4）＋c＝0，解得c＝10，故所求直线方程为2x＋3y＋10＝0.
命题点2 交点与距离问题
例2 （1）[全国卷Ⅲ]点（0，－1）到直线y＝k（x＋1）距离的最大值为（ B ）
A.1B.2C.3D.2
解析 解法一 由点到直线的距离公式知点（0，－1）到直线y＝k（x＋1）的距离d＝｜k+1｜k2+1＝k2+2k+1k2+1＝1+2kk2+1.当k＝0时，d＝1；当k≠0时，d＝1+2kk2+1＝1+2k＋1k，要使d最大，需k＞0且k＋1k最小，由基本不等式知，k＋1k≥2，当且仅当k＝1时，等号成立，所以当k＝1时，dmax＝2，故选B.
解法二 记点A（0，－1），直线y＝k（x＋1）恒过点B（－1，0），当AB垂直于直线y＝k（x＋1）时，点A（0，－1）到直线y＝k（x＋1）的距离最大，且最大值为｜AB｜＝2，故选B.
（2）[2023合肥市期末]若直线y＝x与直线y＝1kx－5的交点在直线y＝kx＋3上，则k的值为 35 .
解析 由题易得k≠1，由y＝1kx－5，y＝x，得x＝y＝5k1－k，将（5k1－k，5k1－k）代入y＝kx＋3，得5k1－k＝5k21－k＋3，得k＝35.
方法技巧
1.求解距离问题的策略
（1）点到直线的距离问题可直接利用距离公式求解，但要注意方程必须为一般式.
（2）两平行线间的距离：①利用两平行线间的距离公式求解；②将两条平行线间的距离转化为一条直线上任意一点到另一条直线的距离.
2.遇到含有平方和、绝对值等形式的代数式时，注意利用距离公式的几何意义求解.
训练2 （1）直线l过点P（1，2），且点A（2，3），B（4，－5）到l的距离相等，则直线l的方程是（ C ）
A.4x＋y－6＝0
B.x＋4y－6＝0
C.3x＋2y－7＝0或4x＋y－6＝0
D.3x＋2y－7＝0或x＋4y－6＝0
解析 显然直线l的斜率存在，故设直线l：y－2＝k（x－1），即kx－y－k＋2＝0，则｜2k－3－k+2｜k2+1＝｜4k+5－k+2｜k2+1⇒k－1＝3k＋7或k－1＋3k＋7＝0⇒k＝－4或k＝－32，所以l的方程为y－2＝－4（x－1），即4x＋y－6＝0或y－2＝－32（x－1），即3x＋2y－7＝0.故选C.
（2）函数f（x）＝x2－2x+2＋x2+2x+2的最小值为 22 .
解析 f（x）＝x2－2x+2＋x2+2x+2＝（x－1）2+1＋（x+1）2+1，所以函数f（x）的几何意义为点P（x，0）与点A（1，1），点B（－1，1）的距离之和，易知点P为x轴上一动点，且当点P在原点时，｜PA｜＋｜PB｜取得最小值22.
命题点3 对称问题
例3 已知直线l：2x－3y＋1＝0，点A（－1，－2）.求：
（1）点A关于直线l的对称点A'的坐标；
（2）直线m：3x－2y－6＝0关于直线l的对称直线m'的方程；
（3）直线l关于点A对称的直线l'的方程.
解析 （1）设A'（x，y），则y+2x+1×23＝－1，2×x－12－3×y－22+1=0，
解得x＝－3313，y＝413，即A'（－3313，413）.
（2）在直线m上任取一点，如M（2，0），则M（2，0）关于直线l的对称点必在m'上.
设M关于直线l的对称点为M'（a，b），
则2×a+22－3×b+02+1=0，b－0a－2×23＝－1，解得a＝613，b＝3013，即M'（613，3013）.设m与l的交点为N，则由2x－3y+1=0，3x－2y－6=0得N（4，3）.
又m'经过点N（4，3），
所以由两点式得直线m'的方程为9x－46y＋102＝0.
（3）解法一 在l：2x－3y＋1＝0上任取两点，如P（1，1），N（4，3），则P，N关于点A的对称点P'，N'均在直线l'上.
易知P'（－3，－5），N'（－6，－7），由两点式可得l'的方程为2x－3y－9＝0.
解法二 设Q（x，y）为l'上任意一点，则Q（x，y）关于点A（－1，－2）的对称点为
Q'（－2－x，－4－y），
因为点Q'在直线l上，所以2（－2－x）－3（－4－y）＋1＝0，即2x－3y－9＝0.
方法技巧
对称问题的解题策略
训练3 （1）[多选/2023江西抚州南城二中模拟]一束光线沿着直线y＝－3x＋3a2－4a－2射到直线x＋y＝0上，经反射后沿着直线y＝－13x－23射出，则实数a可以为（ AD ）
A.2B.－2C.23D.－23
解析 由题知，直线y＝－3x＋3a2－4a－2与直线y＝－13x－23关于直线x＋y＝0对称.在直线y＝－13x－23上任意取一点A（x0，y0），其关于直线x＋y＝0对称的点为（-y0，-x0），则y0＝－13x0－23，－x0=3y0+3a2－4a－2，整理得3a2－4a－4＝0，解得a＝-23或a＝2，故选AD.
（2）过点P（0，1）作直线l，使它被直线l1：2x＋y－8＝0和l2：x－3y＋10＝0截得的线段被点P平分，则直线l的方程为 x＋4y－4＝0 .
解析 设l1与l的交点为A（a，8－2a），由题意知，点A关于点P的对称点B(-a，2a-6)在l2上，把点B的坐标代入l2的方程得－a－3（2a－6）＋10＝0，解得a＝4.因为点A（4，0），P（0，1）在直线l上，所以直线l的方程为x＋4y－4＝0.
1.[命题点1]已知点A（－m－3，2），B（－2m－4，4），C（－m，m），D（3，3m＋2），若直线AB⊥CD，则m的值为 1或－1 .
解析 解法一 ∵A，B两点的纵坐标不相等，∴AB与x轴不平行，
又AB⊥CD，∴CD与x轴不垂直，∴－m≠3，即m≠－3.
当AB与x轴垂直时，－m－3＝－2m－4，解得m＝－1，而当m＝－1时，点C，D的纵坐标均为－1，则CD∥x轴，此时AB⊥CD，满足题意.
当AB与x轴不垂直，即m≠－1时，
kAB＝4－2－2m－4－（－m－3）＝2－（m+1），
kCD＝3m+2－m3－（－m）＝2（m+1）m+3.
∵AB⊥CD，∴kAB·kCD＝－1，
即2－（m+1）·2（m+1）m+3＝－1，解得m＝1.
综上，m的值为1或－1.
解法二 由题意可得AB·CD＝0，所以（－m－1，2）·（3＋m，2m＋2）＝0，解得m＝±1.
2.[命题点2/2023武汉市部分学校质检]在平面直角坐标系中，某菱形的一组对边所在的直线方程分别为x＋2y＋1＝0和x＋2y＋3＝0，另一组对边所在的直线方程分别为3x－4y＋c1＝0和3x－4y＋c2＝0，则｜c1－c2｜＝（ B ）
A.23B.25C.2D.4
解析 直线x＋2y＋1＝0与x＋2y＋3＝0间的距离d1＝｜3－1｜12＋22＝255，
直线3x－4y＋c1＝0与3x－4y＋c2＝0间的距离d2＝｜c1－c2｜32＋（－4）2＝｜c1－c2｜5.由菱形的性质知d1＝d2，所以｜c1－c2｜5＝255，所以｜c1－c2｜＝25.
3.[命题点2]｜3x＋4y－12｜＋｜3x＋4y＋1｜的最小值为 13 .
解析 设点P（x，y），l1：3x＋4y－12＝0，l2：3x＋4y＋1＝0，则点P到l1的距离d1＝｜3x+4y－12｜5，点P到l2的距离d2＝｜3x+4y+1｜5，则｜3x＋4y－12｜＋｜3x＋4y＋1｜＝5（d1＋d2），易得直线l1∥l2，所以当点P位于直线
l1与l2之间时，｜3x＋4y－12｜＋｜3x＋4y＋1｜最小，最小值为直线l1与l2之间的距离的5倍，即d＝|-12-1|5×5＝13.
4.[命题点2，3/2024江西景德镇一中模拟]在平面直角坐标系xOy中，△ABC的顶点A的坐标为（－4，2），AB边上的中线CM所在的直线方程为x－y＋1＝0，∠B的角平分线所在的直线方程为2x＋y－2＝0，则直线BC的方程为 18x－y－38＝0 .
解析 设点B坐标为（a，b），因为点A的坐标为（－4，2），所以AB的中点M（a-42，b+22），所以a－42－b+22＋1＝0，即a－b－4＝0.
因为点B在直线2x＋y－2＝0上，所以2a＋b－2＝0.
由a－b－4=0，2a＋b－2=0，解得a=2，b＝－2，所以B（2，－2）.
设点A （－4，2）关于直线2x＋y－2＝0的对称点为A'（m，n），
则2×m－42＋n+22－2=0，n－2m+4×（－2）＝－1，解得m＝125，n＝265，
所以A'（125，265），所以直线BC的方程为y＋2＝265+2125－2·（x－2），即18x－y－38＝0.
5.[命题点3]已知直线l：x－y－1＝0.若直线l上存在一点P，使P到A（4，1）与B（0，4）的距离之差的绝对值最大，则点P的坐标为 (103,73) ；
若直线l上存在一点Q，使Q到A（4，1）与C（3，0）的距离之和最小，则点Q的坐标为 (52,32) .
解析 如图1，设点B关于l的对称点B'的坐标为（a，b），连接BB'，PB，PB'，
易得b－4a×1=－1，a2－b+42－1=0，解得a=5，b＝－1，∴点B'的坐标为（5，－1）.
易知｜｜PB｜－｜PA｜｜＝｜｜PB'｜－｜PA｜｜≤｜AB'｜，当P，B'，A三点共线时，｜｜PB'｜－｜PA｜｜最大.
于是直线AB'的方程为y－1－1－1＝x－45－4，即2x＋y－9＝0. 图1
联立直线l与AB'的方程，解得x＝103，y＝73，
即点P的坐标为（103，73）.
如图2，设点C关于l的对称点C'的坐标为（m，n），连接CC'，QC，QC'，QA，
易得nm－3×1=－1，m+32－n2－1=0，解得m=1，n=2， 图2
∴点C'的坐标为（1，2），
∴直线AC'的方程为y－12－1＝x－41－4，即x＋3y－7＝0.
易知｜QA｜＋｜QC｜＝｜QA｜＋｜QC'｜≥｜AC'｜，当Q，A，C'三点共线时，｜QA｜＋｜QC'｜最小.
联立直线AC'与l的方程，解得x＝52，y＝32，
即点Q的坐标为（52，32）.
学生用书·练习帮P349
1.[2024山东鄄城第一中学校考]若直线y＝x＋2k＋1与直线y＝－12x＋2的交点在第一象限，则实数k的取值范围是（ A ）
A.（－52，12）B.（－25，12）
C.[－52，－12]D.[－25，12]
解析 将两直线方程联立得y＝x+2k+1，y＝－12x+2，得x＝2－4k3，y＝2k+53，即交点坐标为（2－4k3，2k+53）.因为交点在第一象限，所以2－4k3>0，2k+53>0，解得－52＜k＜12.故选A.
2.[2024天津耀华中学校考]已知A（－2，4），B（－4，6）两点到直线l：ax＋y＋1＝0的距离相等，则a的值为（ A ）
A.1或2B.3或4C.3D.4
解析 由题意得｜－2a+4+1｜a2+1＝｜－4a+6+1｜a2+1，整理得｜2a－5｜＝｜4a－7｜，则2a－5＝±(4a-7)，解得a＝1或a＝2.故选A.
3.已知直线l1：xsin α＋y－1＝0，直线l2：x－3ycs α＋1＝0，若l1⊥l2，则sin 2α＝（ A ）
A.35B.－35C.23D.－23
解析 因为l1⊥l2，所以sin α－3cs α＝0，所以tan α＝3，所以sin 2α＝2sin αcs α＝2sinαcsαsin2α＋cs2α＝2tanα1+tan2α＝35.故选A.
4.[2024河北衡水模拟]已知点（a，b）在线段3x＋4y－10＝0（－2≤x≤6）上，则a2+b2-2的取值范围是（ B ）
A.[2，18]B.[2，38]
C.[0，38]D.[0，210－2]
解析 画出3x＋4y－10＝0（－2≤x≤6）的图象如图.（a，b）是图中线段上任意一点，a2＋b2表示原点到点（a，b）的距离的平方，易知图中线段的端点分别为（－2，4），（6，－2），到原点距离的平方分别为20，40，由原点到线段的距离d＝|-10|32＋42＝2，可得d2＝4，综上，
a2＋b2∈[4，40]，故a2＋b2－2∈[2，38].故选B.
5.已知点A（3，－1），B（5，－2），且点P在直线x＋y＝0上，若使｜PA｜＋｜PB｜取得最小值，则P点的坐标是（ C ）
A.（1，－1）B.（－1，1）
C.（135，－135）D.（－2，2）
解析 点A（3，－1）关于直线x＋y＝0的对称点为A'（1，－3），直线A'B与直线x＋y＝0的交点即为所求的点，直线A'B的方程为y+3－2+3＝x－15－1，即y＝14x－134，与x＋y＝0联立，解得x＝135，y＝－135.
即点P坐标为（135，－135）时，｜PA｜＋｜PB｜取得最小值.
6.m是实数，直线l1：x－my－2＝0与直线l2：mx＋y＋2＝0交于点Q，O为坐标原点，则｜OQ｜的最大值是（ B ）
A.2B.22C.23D.4
解析 解法一 由x－my－2=0，mx＋y+2=0，得x＝2－2mm2+1，y＝－2m+2m2+1，
即点Q（2－2mm2+1，－2m+2m2+1）.
因为m是实数，O为坐标原点，所以｜OQ｜＝2-2mm2+12+-2m+2m2+12=8(m2+1)m2+12=22m2+1，则当m＝0时，｜OQ｜max＝22，所以｜OQ｜的最大值是22.
解法二 易知直线l1恒过定点A（2，0），直线l2恒过定点B（0，－2），且l1⊥l2.连接AB，数形结合（如图所示）可知，点O，Q均在以AB为直径的圆上，故可得｜OQ｜max＝｜AB｜＝22.
7.[多选/2023青岛检测]已知直线l1：4x－3y＋4＝0，l2：（m＋2）x－（m＋1）y＋2m＋5＝0（m∈R），则（ ACD ）
A.直线l2过定点（－3，－1）
B.当m＝1时，l1⊥l2
C.当m＝2时，l1∥l2
D.当l1∥l2时，两直线l1，l2之间的距离为1
解析 对于A，解法一 直线l2的方程可化为2x－y＋5＋m（x－y＋2）＝0，由2x－y+5=0，x－y+2=0，解得x＝－3，y＝－1，即直线l2过定点（－3，－1），故A正确.
解法二 在直线l2的方程中分别令m＝－1与m＝－2，得x＋3＝0，y＋1＝0，即x＝－3，y＝－1，所以直线l2过定点（－3，－1），故A正确.
对于B，若l1⊥l2，则有4（m＋2）＋（－3）·[－（m＋1）]＝0，解得m＝－117，故B不正确.
对于C，若l1∥l2，则有4·[－（m＋1）]－（－3）·（m＋2）＝0，解得m＝2，当m＝2时，l1与l2不重合，故C正确.
对于D，当l1∥l2时，由对选项C的分析可得此时直线l2的方程为4x－3y＋9＝0，则l1，l2之间的距离为｜4－9｜42＋（－3）2＝1，故D正确.故选ACD.
8.[2024安徽合肥联考]过直线2x－y＋4＝0与3x－2y＋9＝0的交点，且垂直于直线x-2y+1＝0的直线方程是 2x＋y－8＝0 .
解析 由3x－2y+9=0，2x－y+4=0，解得x=1，y=6，即交点坐标为（1，6）.因为所求直线与直线x－2y＋1＝0垂直，所以所求直线的斜率为－112＝－2，所以所求的直线方程是y－6＝－2（x－1），即2x＋y－8＝0.
9.已知△ABC的一个顶点A（4，－1），两条角平分线所在直线的方程分别为l1:x－y－1=0和l2：x－1＝0，则BC边所在直线的方程为 2x－y＋3＝0 .
解析 由题知，A（4，－1）不在这两条角平分线上，因此l1，l2是角B，角C的角平分线所在直线.设点A关于直线l1的对称点为A1（x1，y1），关于直线l2的对称点为A2（x2，y2），则A1，A2均在边BC所在的直线上.由y1+1x1－4×1=－1，x1+42－y1－12－1=0，得x1=0，y1=3，所以A1(0,3).因为l2：x＝1，所以易得y2＝－1，由x2+42＝1，得x2＝－2，所以A2（－2，－1）.所以BC边所在直线的方程为y－3－1－3＝x－0－2－0，即2x－y＋3＝0.
10.过点A（0，73），B（7，0）的直线l1与过点（2，1），（3，k＋1）的直线l2和两坐标轴围成的四边形内接于一个圆，则实数k＝（ B ）
A.－3B.3C.－6D.6
解析 若l1和l2与两坐标轴围成的四边形内接于一个圆，则l1⊥l2.（圆内接四边形的对角互补）
易知直线l1的斜率k1=73-7=-13，直线l2的斜率k2＝k+1－13－2＝k，由k1k2＝－1，得k＝3.
11.在平面直角坐标系中，记d为点P（cs θ，sin θ）到直线x－my－2＝0的距离.当θ，m变化时，d的最大值为（ C ）
A.1B.2C.3D.4
解析 解法一 由题意可得d＝｜csθ－msinθ－2｜m2+1＝｜msinθ－csθ+2｜m2+1＝｜m2+1（mm2+1sinθ－1m2+1csθ）+2｜m2+1＝｜m2+1sin（θ－φ）+2｜m2+1（其中cs φ＝mm2+1，sin φ＝1m2+1），∵－1≤sin（θ－φ）≤1，∴｜2－m2+1｜m2+1≤d≤m2+1+2m2+1＝1＋2m2+1，∴当m＝0时，d取得最大值3，故选C.
解法二 易知点P（cs θ，sin θ）在单位圆x2＋y2＝1上，直线x－my－2＝0恒过定点A（2，0）.如图所示，作OB垂直该直线，垂足为B，则由图可知d≤｜OB｜＋r≤｜OA｜＋r＝2＋1＝3（其中r是单位圆的半径），所以dmax＝3，此时A，B重合，直线方程为x＝2.
12.[多选/2024山西吕梁统考]已知点A（－2，1），B（1，1），且点P在直线l:x+y+3=0上，则（ ACD ）
A.存在点P，使得｜PA｜＝2
B.存在点P，使得PA⊥PB
C.存在点P，使得2｜PA｜＝｜PB｜
D.｜PA｜＋｜PB｜的最小值为29
解析 设P（a，－a－3）.对于A，若｜PA｜＝2，则(a+2)2＋(－a－3－1)2＝2，即a2+6a+8=0，解得a＝－2或a＝－4，故存在点P，使得｜PA｜＝2，A正确.
对于B，当a＝－2时，直线PA的斜率不存在，又kPB＝23≠0，此时PA与PB不垂直；当a=1时，直线PB的斜率不存在，又kPA＝－53≠0，此时PA与PB不垂直；当a≠－2且a≠1时，kPA＝－a－4a+2，kPB＝－a－4a－1，若PA⊥PB，则kPAkPB＝－a－4a+2·－a－4a－1＝－1，即2a2＋9a＋14＝0，Δ＝92－4×2×14＝－31＜0，方程无解，故不存在点P，使得PA⊥PB，B错误.
对于C，若2｜PA｜＝｜PB｜，则2（a+2）2＋（－a－3－1）2＝（a－1）2＋（－a－3－1）2，即2a2＋14a＋21＝0，Δ＝142－4×2×21＝28＞0，方程有解，故存在点P，使得2｜PA｜＝｜PB｜，C正确.
对于D，设A（－2，1）关于直线l的对称点为A'（a，b），则b－1a+2=1，－2+a2＋1+b2+3=0，解得a＝－4，b＝－1，所以A'（－4，－1），所以｜PA｜＋｜PB｜＝｜PA'｜＋｜PB｜≥｜A'B｜＝（－4－1）2＋（－1－1）2＝29，当且仅当A'，P，B三点共线时取等号，故D正确.
故选ACD.
13.已知点A（5，0），B（0，4），动点P，Q分别在直线y＝x＋2和y＝x上，且PQ与两直线垂直，则｜AQ｜＋｜QP｜＋｜PB｜的最小值为 5＋2 .
解析 设Q（x0，x0），因为直线PQ与两直线垂直，所以｜PQ｜＝2，则P（x0－1，x0＋1），故｜AQ｜＋｜BP｜＝(x0－5)2＋x02＋(x0-1)2＋(x0－3)2，此式可理解为点Q(x0，x0)到A（5，0）及C（1，3）的距离之和，其最小值为｜AC｜＝5.故AQ+QP+|PB|的最小值为5＋2.
14.[新定义题]定义点P（x0，y0）到直线l：ax＋by＋c＝0（a2＋b2≠0）的有向距离为d＝ax0＋by0＋ca2＋b2.已知点P1，P2到直线l的有向距离分别是d1，d2，给出以下命题，其中是真命题的是（ D ）
A.若d1－d2＝0，则直线P1P2与直线l平行
B.若d1＋d2＝0，则直线P1P2与直线l平行
C.若d1＋d2＝0，则直线P1P2与直线l垂直
D.若d1d2＜0，则直线P1P2与直线l相交
解析 设P1（x1，y1），P2（x2，y2），若d1＝d2＝0，满足d1－d2＝0，d1＋d2＝0，则ax1＋by1＋c＝ax2＋by2＋c，直线P1P2与直线l重合，A，B，C错误；对于D，若d1d2＜0，即（ax1＋by1＋c）（ax2＋by2＋c）＜0，所以点P1，P2分别位于直线l的两侧，所以直线P1P2与直线l相交，D正确.课标要求
命题点
五年考情
命题分析预测
1.能根据斜率判定两条直线平行或垂直.
2.能用解方程组的方法求两条相交直线的交点坐标.
3.探索并掌握平面上两点间及点到直线的距离公式，会求两条平行直线间的距离.
两条直线的位置关系
该讲知识是平面解析几何部分的基础，命题热点为两点间与点到直线的距离公式的应用，判断两直线的位置关系及求解有关对称问题，一般以选择题和填空题的形式出现，难度中等偏易.
交点与距离问题
2021新高考卷ⅠT11；2021新高考卷ⅡT3；2020全国卷ⅡT5；2020全国卷ⅢT8
对称问题
2022新高考卷ⅡT15
斜截式
一般式
方程
y＝k1x＋b1，y＝k2x＋b2.
A1x＋B1y＋C1＝0（A12＋B12≠0），A2x＋B2y＋C2＝0（A22＋B22≠0）.
垂直
① k1k2＝－1 .
② A1A2＋B1B2＝0 .
平行
③ k1＝k2且b1≠b2 .
A1B2－A2B1=0，B1C2－B2C1≠0或A1B2－A2B1=0，A1C2－A2C1≠0.
重合
k1＝k2且b1＝b2.
A1B2－A2B1＝B1C2－B2C1＝A1C2－A2C1＝0.
距离类型
公式
两点P1（x1，y1），P2（x2，y2）间的距离｜P1P2｜.
｜P1P2｜＝④ (x2－x1)2＋(y2－y1)2 .
点P0（x0，y0）到直线l：Ax＋By＋C＝0的距离d.
d＝⑤ |Ax0+By0+C|A2+B2 .
两条平行直线Ax＋By＋C1＝0与Ax＋By＋C2＝0间的距离d.
d＝⑥ |C1-C2|A2+B2 .
点关于
点对称
若点M（x1，y1）和点N（x，y）关于点P（a，b）对称，则由中点坐标公式得x=2a－x1，y=2b－y1，进而求解.
直线关于
点对称
直线关于点对称的问题可转化为点关于点对称的问题.
点关于
直线
对称
若两点P1（x1，y1）与P2（x2，y2）（x1≠x2）关于直线l：Ax＋By＋C＝0（B≠0）对称，则有P1P2的中点在l上，P1P2⊥l，即A·x1＋x22＋B·y1＋y22＋C=0，y2－y1x2－x1·（－AB）＝－1.
直线关于
直线对称
直线关于直线的对称问题可转化为点关于直线的对称问题.