备战2025年高考数学精品教案第六章平面向量、复数第5讲解三角形应用举例（Word版附解析）

这是一份备战2025年高考数学精品教案第六章平面向量、复数第5讲解三角形应用举例（Word版附解析），共9页。
学生用书P129
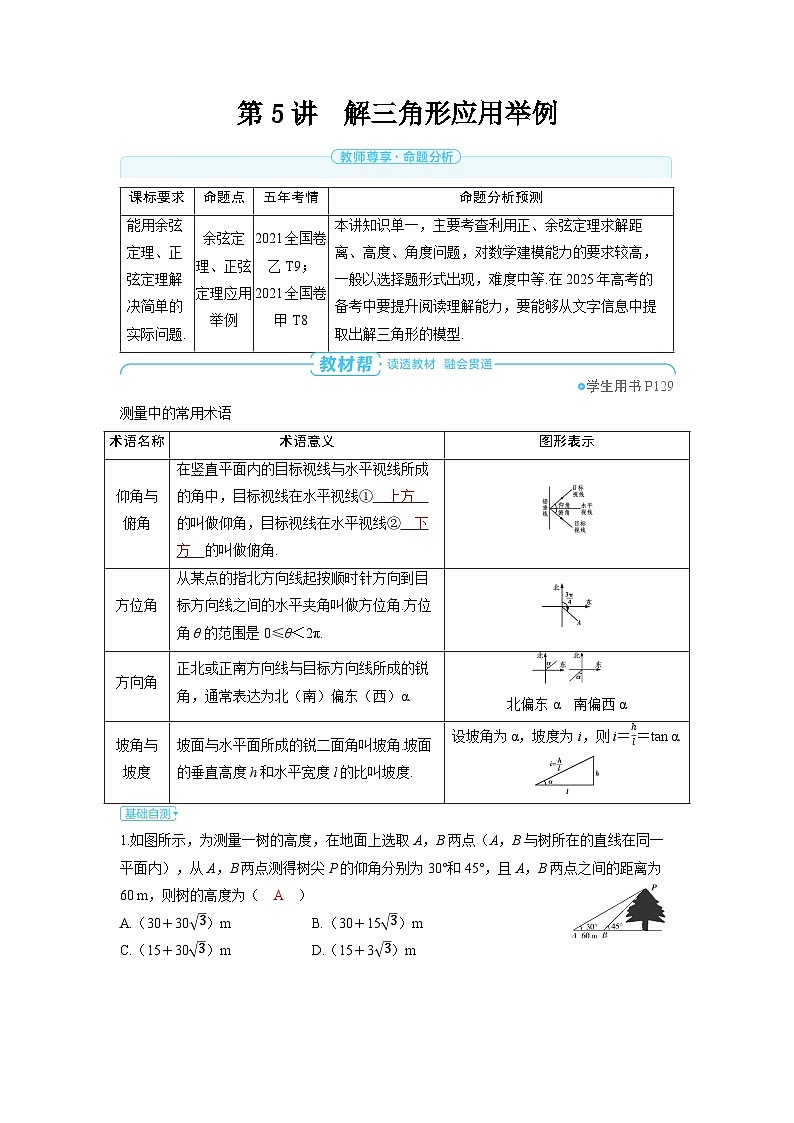
测量中的常用术语
1.如图所示，为测量一树的高度，在地面上选取A，B两点（A，B与树所在的直线在同一平面内），从A，B两点测得树尖P的仰角分别为30°和45°，且A，B两点之间的距离为60 m，则树的高度为（ A ）
A.（30＋303）mB.（30＋153）m
C.（15＋303）mD.（15＋33）m
解析 解法一 在△ABP中，由正弦定理可得60sin（45°－30°）＝PBsin30°，则PB＝60×12sin15°＝30（6＋2）.
设树的高度为h m，则h＝PBsin 45°＝30＋303.
解法二 设树的高度为h m，则AB＝htan30°－htan45°＝60，解得h＝30＋303.
2.[易错题]两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站北偏东40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的（ B ）
A.北偏东10°B.北偏西10°C.南偏东10°D.南偏西10°
解析 灯塔A，B的相对位置如图所示，由已知得∠ACB＝80°，∠CAB＝∠CBA＝50°，则α＝60°－50°＝10°，即北偏西10°，故选B.
3.[教材改编]已知A船在灯塔C的北偏东85°方向且A到C的距离为2 km，B船在灯塔C的西偏北25°方向且B到C的距离为3 km，则A，B两船的距离为（ A ）
A.13 kmB.15 kmC.23 kmD.32 km
解析 画出图形如图所示，由题意可得∠ACB＝（90°－25°）＋85°＝150°，又AC＝2，BC＝3，在△ABC中，由余弦定理可得AB2＝AC2＋BC2－2AC·BC·cs 150°＝13，所以AB＝13，即A，B两船的距离为13 km.
学生用书P130
命题点 余弦定理、正弦定理应用举例
角度1 距离问题
例1 [2023合肥市二检]如图，某地需要经过一座山两侧的D，E两点修建一条穿山隧道.工程人员先选取直线DE上的三点A，B，C，在隧道DE正上方的山顶P处测得A处的俯角为15°，B处的俯角为45°，C处的俯角为30°，且测得AB＝1.4 km，BD＝0.2 km，CE＝0.5 km，则拟修建的隧道DE的长为 0.7km .
解析 由题意知，∠PAB＝15°，∠PBC＝45°，∠PCB＝30°，所以∠APB＝∠PBC－∠PAB＝30°，∠BPC＝180°－∠PBC－∠PCB＝105°，在△PAB中，由正弦定理得ABsin∠APB＝PBsin∠PAB，则1.4sin30°＝PBsin15°，所以PB＝2.8sin 15°（km）.
在△PBC中，由正弦定理得PBsin∠PCB＝BCsin∠BPC，则PBsin30°＝BCsin105°，所以BC＝PBsin30°×sin 105°＝2PB×sin 105°＝5.6sin 15°·sin 105°＝5.6sin 15°cs 15°＝2.8sin 30°＝1.4（km），所以DE＝BC－BD－EC＝1.4－0.2－0.5＝0.7（km），
即拟修建的隧道DE的长为0.7 km.
角度2 高度问题
例2 [2021全国卷甲]2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86 （单位：m），三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影A'，B'，C'满足∠A'C'B'＝45°，∠A'B'C'＝60°.由C点测得B点的仰角为15°，BB'与CC'的差为100；由B点测得A点的仰角为45°，则A，C两点到水平面A'B'C'的高度差AA'－CC'约为（3≈1.732）（ B ）
A.346B.373C.446D.473
解析 如图所示，根据题意过C作CE∥C'B'，交BB'于E，过B作BD∥A'B'，交AA'于D，则BE＝100，C'B'＝CE＝100tan15°.
在△A'C'B'中，∠C'A'B'＝75°，则 BD＝A'B'＝C'B'×sin45°sin75°.又在B点处测得A点的仰角为45°，所以AD＝BD＝C'B'×sin45°sin75°，所以高度差AA'－CC'＝AD＋BE＝C'B'×sin45°sin75°＋100＝100tan15°×sin45°sin75°＋100＝100sin45°sin15°＋100＝100×226－24＋100＝100（3＋1）＋100≈373.故选B.
角度3 角度问题
例3 如图所示，位于A处的信息中心获悉：在其正东方向40海里的B处有一艘渔船遇险，在原地等待营救.信息中心立即把消息告知在其南偏西30°，相距20海里的C处的乙船，现乙船朝北偏东θ的方向即沿直线CB前往B处救援，则cs θ＝ 2114 .
解析 在△ABC中，AB＝40，AC＝20，∠BAC＝120°.
由余弦定理，得BC2＝AB2＋AC2－2AB·AC·cs 120°＝2 800，所以BC＝207.
由正弦定理，得sin∠ACB＝ABBC·sin∠BAC＝217.
由∠BAC＝120°，知∠ACB为锐角，故cs∠ACB＝277，从而cs θ＝cs（∠ACB＋30°）＝cs∠ACBcs 30°－sin∠ACBsin 30°＝277×32－217×12＝2114.
方法技巧
1.解三角形实际问题的一般求解步骤
（1）分析.理解题意，分析已知与未知，画出示意图.
（2）建模.根据已知条件与求解目标，把已知量与所求量尽量集中在相关的三角形中，建立一个解三角形的模型.
（3）求解.利用正、余弦定理解三角形，求得数学模型的解.
（4）检验.检验上述所求出的解是否具有实际意义，从而得出实际问题的解.
2.对于立体测量问题，通常要转化为两类平面问题，一类是竖直放置的平面，通常要解直角三角形；另一类是水平放置的平面，通常要解斜三角形.
训练 （1）如图，为测量某塔的高度CD，在点A测得塔底在北偏东60°方向的点D处，塔顶C的仰角为30°.在点A的正东方向且距离D点50 m的B点测得塔底在北偏西45°方向，则塔的高度CD约为（参考数据：6≈2.4）（ C ）
A.30 mB.35 mC.40 mD.45 m
解析 由题意知，BD＝50 m，∠DAB＝∠DAC＝30°，∠DBA＝45°，在△ABD中，由正弦定理得ADsin45°＝50sin30°，则AD＝502 m，所以tan∠DAC＝CDAD＝CD502＝33，得CD＝5063≈
40（m），故塔的高度CD约为40 m.故选C.
（2）[多选]一艘轮船航行到A处时看灯塔B在A的北偏东75°方向，距离为126 海里，灯塔C在A的北偏西30°方向，距离为123 海里，该轮船由A沿正北方向继续航行到D处时再看灯塔B在其南偏东60°方向，则下列结论正确的有（ ABD ）
A.AD＝24海里
B.CD＝12海里
C.∠CDA＝60°或∠CDA＝120°
D.∠CDA＝60°
解析 如图，由题意得∠BAD＝75°，∠CAD＝30°，∠ADB＝60°，AB＝126海里，AC＝123海里，在△ABD中，易得B＝45°，由正弦定理得ADsin45°＝ABsin60°，则AD＝126×2232＝24（海里），故A正确.在△ACD中，由余弦定理得CD2＝AC2＋AD2－2×AC×AD×cs 30°，得CD2＝（123）2＋242－2×123×24×32＝144，所以CD＝12海里，故B正确.在△ACD中，由正弦定理得CDsin30°＝ACsin∠CDA，得sin∠CDA＝12×12312＝32，故∠CDA＝60°或∠CDA＝120°，因为AD＞AC，所以∠CDA为锐角，所以∠CDA＝60°，故C错误，D正确.故选ABD.
1.[角度1]如图，曲柄连杆机构中，曲柄CB绕C点旋转时，通过连杆AB的传递，使活塞做直线往复运动.当曲柄在CB0位置时，曲柄和连杆成一条直线，连杆的端点A在A0处.设连杆AB长200 mm，曲柄CB长70 mm，则曲柄自CB0按顺时针方向旋转53.2°时，活塞移动的距离（即连杆的端点A移动的距离A0A）约为 36 mm.（结果保留整数，取sin 53.2°＝45）
解析 解法一 在△ABC中，AB＝200 mm，BC＝70 mm，∠ACB＝53.2°，sin∠ACB＝45.由正弦定理得sin∠BAC＝BCsin∠ACBAB＝725，由题意知∠BAC，∠ACB均为锐角，所以cs∠BAC＝1－（725）2＝2425，cs∠ACB＝1－（45）2＝35，所以sin∠ABC＝sin（∠ACB＋∠BAC）＝45×2425＋35×725＝117125，所以AC＝ABsin∠ABCsin∠ACB＝200×117125×54＝234（mm），故A0A＝（A0B0＋B0C）－AC＝（200＋70）－234＝36（mm），即曲柄自CB0按顺时针方向旋转
53.2°时，活塞移动的距离约为36 mm.
解法二 因为∠ACB＝53.2°，sin∠ACB＝45，且∠ACB为锐角，所以cs∠ACB＝1－sin2∠ACB＝35.在△ABC中，由余弦定理可得AB2＝AC2＋BC2－2×AC×BCcs∠ACB，解得AC＝234 mm（负值舍去），故A0A＝（A0B0＋B0C）－AC＝（200＋70）－234＝36（mm），即曲柄自CB0按顺时针方向旋转53.2°时，活塞移动的距离约为36 mm.
2.[角度2]如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点，从点A测得点M的仰角∠MAN＝60°，点C的仰角∠CAB＝45°以及∠MAC＝75°；从点C测得∠MCA＝60°，已知山高BC＝100 m，则山高MN＝ 150 m.
解析 在△ABC中，因为∠BAC＝45°，∠ABC＝90°，BC＝100，所以AC＝100sin45°＝1002.在△AMC中，因为∠MAC＝75°，∠MCA＝60°，所以∠AMC＝45°，由正弦定理可得AMsin60°＝1002sin45°，解得AM＝1003.在Rt△AMN中，MN＝AM·sin∠MAN＝1003×sin 60°＝150.所以山高MN为150 m.
学生用书·练习帮P325
1. [2024黑龙江省实验中学开学考试]中国古代四大名楼之一鹳雀楼，位于山西省运城市永济市蒲州镇，因唐代诗人王之涣的诗作《登鹳雀楼》而闻名遐迩.如图，某同学为测量鹳雀楼的高度MN，在鹳雀楼的正东方向找到一座建筑物AB，高约为37 m，在地面上点C处（B，C，N三点共线）测得建筑物顶部A，鹳雀楼顶部M的仰角分别为30°和45°，在A处测得鹳雀楼顶部M的仰角为15°，则鹳雀楼的高度MN约为（ B ）
A.64 mB.74 mC.52 mD.91 m
解析 在Rt△ABC中，AB⊥BC，AB＝37，∠ACB＝30°，所以AC＝2AB＝74，在Rt△MNC中，NC⊥MN，∠MCN＝45°，所以MN＝MC·sin 45°＝22MC.由题意，∠MAC＝15°＋30°＝45°，∠MCA＝180°－45°－30°＝105°，故∠AMC＝180°－105°－45°＝30°.在△ACM中，由正弦定理MCsin∠MAC＝ACsin∠AMC，得MCsin45°＝74sin30°，故MC＝74sin45°sin30°＝742，所以MN＝22×742＝74，故选B.
2. [设问创新/多选/2024江苏南通阶段检测]重庆的解放碑是重庆的地标性建筑，吸引了众多游客打卡拍照.某中学数学兴趣小组对解放碑的高度进行测量，并绘制出测量方案示意图，如图所示，A为解放碑的顶端，B为基座（B在A的正下方），在步行街（与B在同一水平面内）上选取C，D两点，测得CD的长为100 m.小组成员利用测角仪已测得∠ACB＝π6，则根据下列各组中的测量数据，能计算出解放碑高度AB的是（ ABD ）
A.∠BCD，∠BDCB.∠ACD，∠ADC
C.∠BCD，∠ACDD.∠BCD，∠ADC
解析 对于A，根据CD，∠BCD，∠BDC，可解三角形求得CB，从而在Rt△ABC中求得AB，所以A符合题意.
对于B，根据CD，∠ACD，∠ADC，可解三角形求得AC，从而在Rt△ABC中求得AB，所以B符合题意.
对于C，根据CD，∠ACB，∠BCD，∠ACD四个条件，无法通过解三角形求得AB，所以C不符合题意.
对于D，第一步，∠ACB已知，在Rt△ABC中，用AB表示出BC，AC；第二步，在△BCD中，根据余弦定理用AB表示出BD，在△ACD中，根据正弦定理用AB表示出AD；第三步，在Rt△ABD中，利用勾股定理列方程，即可求得AB.所以D符合题意.
3. [2023皖豫名校联考]如图，一艘巡逻船由南向北行驶，在A处测得某山的底部C在北偏东15°方向上，匀速向北航行20 min到达B处，此时测得该山的底部C在北偏东60°方向上，测得山顶P（P在C正上方）的仰角为60°，已知山的高度为23 km.则巡逻船的航行速度为 6（3＋1） km/h.
解析 由题意知，在△BCP中，PC＝23 km，∠PBC＝60°，故tan∠PBC＝PCBC＝3，得BC＝2 km.在△ABC中，∠BCA＝60°－15°＝45°，则BCsin∠BAC＝ABsin∠BCA，即2sin 15°＝ABsin 45°，而sin 15°＝sin（45°－30°）＝6－24，所以AB＝2×46－2＝2（3＋1）（km）.所以巡逻船的航行速度为2（3＋1）÷13＝6（3＋1）（km/h）.
4.[2023郑州一中期中]如图所示，遥感卫星发现某海域上有三个小岛，小岛B位于小岛A北偏东75°的60海里处，在小岛B北偏东15°方向上，相距（303－30）海里处有一个小岛C.
（1）求小岛A与小岛C之间的距离；
（2）如果有游客想直接从小岛A出发到小岛C，求游船航行的方向.
解析 （1）在△ABC中，AB＝60，BC＝303－30，∠ABC＝180°－75°＋15°＝120°，根据余弦定理得，AC2＝AB2＋BC2－2AB·BC·cs∠ABC＝602＋（303－30）2－2×60×
（303－30）×cs 120°＝5 400，得AC＝306，
∴小岛A与小岛C之间的距离是306海里.
（2）根据正弦定理得，ACsin∠ABC＝ABsin∠ACB，
∴306sin120°＝60sin∠ACB，得sin∠ACB＝22，
又∵0°＜∠ACB＜60°，∴∠ACB＝45°，
∴∠CAB＝180°－120°－45°＝15°.
由75°－15°＝60°得，游船应该沿北偏东60°的方向航行.
5.[2023贵州诊断]镜面反射法是测量建筑物高度的重要方法，在如图所示的模型中，已知人眼距离地面高度h＝1.5 m，某建筑物高h1＝4.5 m，将镜子（平面镜）置于平地上，人后退至从镜中能够看到建筑物顶部的位置，测量人与镜子间的距离a1＝1.2 m，将镜子后移
a m，重复前面的操作，测量人与镜子间的距离a2＝3.2 m，则a＝（ A ）
A.6 B.5 C.4 D.3
解析 如图，设建筑物最高点为A，建筑物底部为O，第一次观察时镜面位置为B，第一次观察时人眼睛位置为C，第二次观察时镜面位置为D，设O到B之间的距离为a0 m，
由光线反射性质得∠ABO＝∠CBD，所以tan∠ABO＝tan∠CBD，即h1a0＝ha1 ①，同理可得h1a0＋a＝ha2 ②，
由①②可得a0＋aa0＝a2a1，解得a0＝a1·aa2－a1，代入①整理得a＝h1（a2－a1）h＝4.5×（3.2－1.2）1.5＝6，故选A.
6.[背景创新]1471年，德国数学家米勒向诺德尔教授提出一个问题：在地球表面的什么部位，一根垂直的悬杆呈现最长（即视角最大，视角是指由物体两端引出的两条光线在眼球内交叉而成的角）？这个问题被称为米勒问题，诺德尔教授给出解答，以悬杆的延长线和水平地面的交点为圆心，悬杆两端点到地面的距离的积的算术平方根为半径在地面上作圆，则圆上的点对悬杆视角最大.米勒问题在实际生活中应用十分广泛.某人观察一座山顶上的铁塔，塔高90 m，山高160 m，此人站在对塔“最大视角”（忽略人身高）的水平地面位置观察此塔，则此时“最大视角”的正弦值为（ B ）
A.12B.941C.1625D.916
解析 如图，由诺德尔教授对米勒问题的解答，设此时的视角为θ，易知塔底距离地面的高度为BC＝160 m，塔顶离地面的高度为AC＝90＋160＝250（m），则人距塔的距离CD＝AC·BC＝200 m，由∠C＝90°得BD＝BC2＋CD2＝4041（m），
AD＝AC2＋CD2＝5041（m），则在△ABD中cs θ＝AD2＋BD2－AB22AD·BD＝4041，故sin θ＝1－cs2θ＝1－（4041）2＝941.故选B.
7.[2024青岛市检测]海洋蓝洞是地球罕见的自然地理现象，被誉为“地球给人类保留宇宙秘密的最后遗产”.若要测量如图所示某蓝洞口边缘A，B两点间的距离，现在珊瑚群岛上取两点C，D，测得CD＝8海里，∠ADB＝135°，∠BDC＝∠DCA＝15°，∠ACB＝120°，则A，B两点间的距离为 85 海里.
解析 如图所示，在△ACD中，∠ADC＝∠ADB＋∠BDC＝135°＋15°＝150°，∠DCA＝15°，则∠DAC＝180°－150°－15°＝15°，即△ACD为等腰三角形，又CD＝8，所以AD＝8.在△BCD中，∠BDC＝15°，∠DCB＝∠DCA＋∠ACB＝15°＋120°＝135°，则∠DBC＝180°－15°－135°＝30°，又CD＝8，所以由BDsin∠DCB＝CDsin∠DBC，得BDsin135°＝8sin30°，所以BD＝82.在△ABD中，AD＝8，BD＝82，∠ADB＝135°，所以AB2＝AD2＋BD2－2AD·BD·cs∠ADB＝82＋（82）2－2×8×82×（－22）＝82×5，所以AB＝85海里.
8.[2024北京市密云二中月考]某自然保护区为研究动物种群的生活习性，设立了两个相距12 km的观测站A和B，观测人员分别在A，B处观测该动物种群.如图，某一时刻，该动物种群出现在点C处，观测人员从两个观测站分别测得∠BAC＝30°，∠ABC＝60°，经过一段时间后，该动物种群出现在点D处，观测人员从两个观测站分别测得∠BAD＝75°，∠ABD＝45°.（注：点A，B，C，D在同一平面内）
（1）求△ABD的面积；
（2）求点C，D之间的距离.
解析 （1）在△ABD中，∠BAD＝75°，∠ABD＝45°，所以∠ADB＝60°.
由正弦定理ADsin∠ABD＝ABsin∠ADB，得ADsin45°＝ABsin60°，
所以AD＝sin45°sin60°·AB＝2232×12＝46（km）.
因为sin∠BAD＝sin 75°＝sin（45°＋30°）＝22×（32＋12）＝6＋24，
所以△ABD的面积S△ABD＝12AB·AD·sin∠BAD
＝12×12×46×6＋24
＝（36＋123）（km2）.
（2）由∠BAD＝75°，∠BAC＝30°，∠ABC＝60°，得∠CAD＝45°，AC＝32AB＝63（km）.
在△ACD中，由余弦定理，得CD2＝AC2＋AD2－2AC·AD·cs∠CAD＝36×3＋16×6－2×63×46×22＝60.
所以CD＝60＝215（km）.
即点C，D之间的距离为215 km.课标要求
命题点
五年考情
命题分析预测
能用余弦定理、正弦定理解决简单的实际问题.
余弦定理、正弦
定理应用举例
2021全国卷乙T9；
2021全国卷甲T8
本讲知识单一，主要考查利用正、余弦定理求解距离、高度、角度问题，对数学建模能力的要求较高，一般以选择题形式出现，难度中等.在2025年高考的备考中要提升阅读理解能力，要能够从文字信息中提取出解三角形的模型.
术语名称
术语意义
图形表示
仰角与
俯角
在竖直平面内的目标视线与水平视线所成的角中，目标视线在水平视线① 上方 的叫做仰角，目标视线在水平视线② 下方 的叫做俯角.
方位角
从某点的指北方向线起按顺时针方向到目标方向线之间的水平夹角叫做方位角.方位角θ的范围是0≤θ＜2π.
方向角
正北或正南方向线与目标方向线所成的锐角，通常表达为北（南）偏东（西）α.
北偏东α 南偏西α
坡角与
坡度
坡面与水平面所成的锐二面角叫坡角.坡面的垂直高度h和水平宽度l的比叫坡度.
设坡角为α，坡度为i，则i＝hl＝tan α.