备战2025年高考数学精品教案第二章函数第4讲幂函数、指数与指数函数（Word版附解析）

这是一份备战2025年高考数学精品教案第二章函数第4讲幂函数、指数与指数函数（Word版附解析），共17页。
学生用书P029
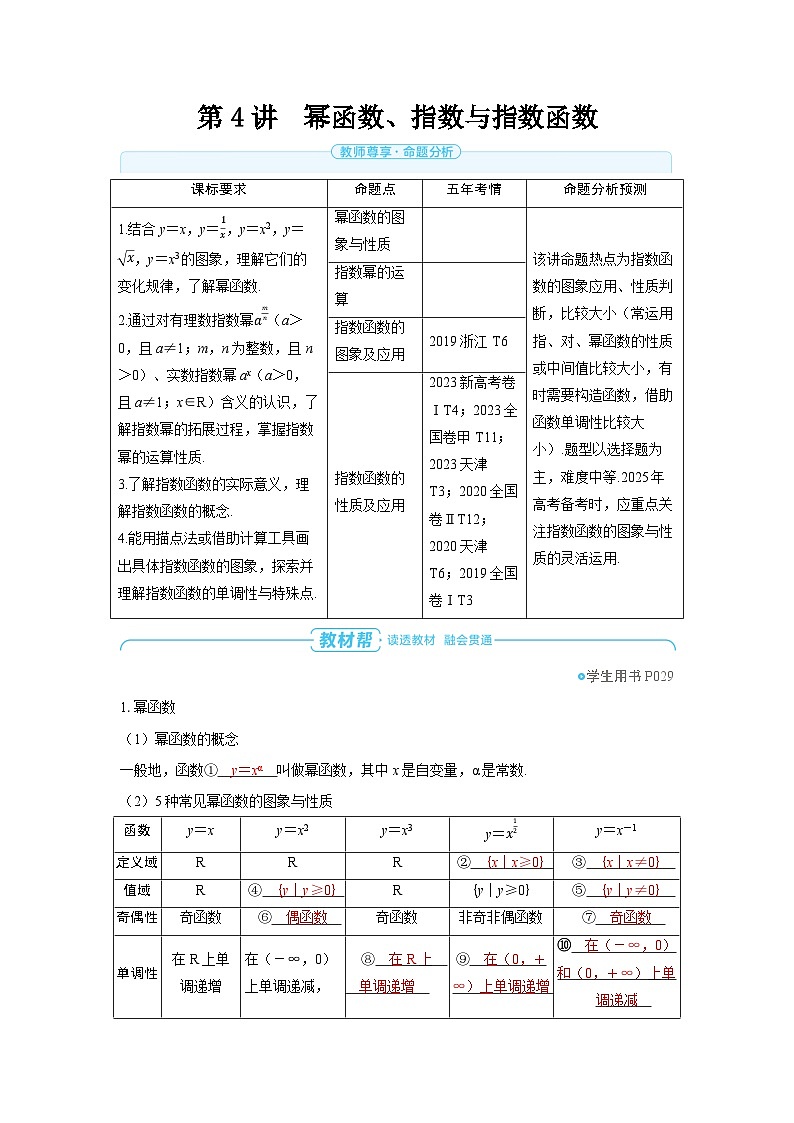
1.幂函数
（1）幂函数的概念
一般地，函数① y＝xα 叫做幂函数，其中x是自变量，α是常数.
（2）5种常见幂函数的图象与性质
规律总结
（1）幂函数y＝xα在第一象限的图象如图所示，可根据函数的定义域以及奇偶性判断幂函数在第二或第三象限的图象.
（2）在（0，1）上，幂函数的指数越大，函数图象越接近x轴；在（1，＋∞）上，幂函数的指数越小，函数图象越接近x轴.
注意 幂函数的图象一定会出现在第一象限，一定不会出现在第四象限，若与坐标轴有交点，则交点一定是原点.
2.指数与指数运算
（1）根式
a.（na）n＝⑫ a （n∈N*，且n＞1）.
b.nan＝a，n为奇数，｜a|,n为偶数.
（2）分数指数幂
a.amn＝⑬ nam （a＞0，m，n∈N*，且n＞1）.
b.a－mn＝1amn＝⑭ 1nam （a＞0，m，n∈N*，且n＞1）.
注意 0的正分数指数幂等于0，0的负分数指数幂没有意义.
（3）有理数指数幂的运算性质
a.ar·as＝⑮ ar＋s （a＞0，r，s∈R）；aras＝⑯ ar－s （a＞0，r，s∈R）；
b.（ar）s＝⑰ ars （a＞0，r，s∈R）；
c.（ab）r＝⑱ arbr （a＞0，b＞0，r∈R）.
3.指数函数
（1）指数函数的概念
函数y＝ax（a＞0，且a≠1）叫做指数函数，其中指数x是自变量，定义域是R.
（2）指数函数的图象和性质
注意 当指数函数的底数a的大小不确定时，需分a＞1和0＜a＜1两种情况进行讨论.
规律总结
1.指数函数的图象过点（0，1），（1，a），（－1，1a），依据这三点的坐标可得到指数函数的大致图象.
2.函数y＝ax（a＞0，且a≠1）的图象与y＝a－x的图象关于y轴对称，y＝ax的图象与y＝－ax的图象关于x轴对称，y＝ax的图象与y＝－a－x的图象关于坐标原点对称.
3.如图，底数a，b，c，d与1之间的大小关系为0＜c＜d＜1＜a＜b.
1.[2024江苏省南通市质量监测]化简：（π－4）2＋3（π－3）3＝（ A ）
A.1B.－1C.7－2πD.2π－7
解析 （π－4）2＋3（π－3）3＝｜π－4｜＋π－3＝4－π＋π－3＝1.故选A.
2.[多选]已知幂函数f（x）＝xα的图象经过点（16，4），则下列说法正确的有（ BCD ）
A.f（x）是偶函数B.f（x）是增函数
C.当x＞1时，f（x）＞1D.当0＜x1＜x2时，f（x1）＋f（x2）2＜f（x1＋x22）
解析 因为幂函数f（x）＝xα的图象经过点（16，4），所以16α＝4，α＝12，所以f（x）＝x12＝x，由其图象可知，A错误，B正确；当x＞1时，f（x）＞f（1）＝1，故C正确；由f（x）＝x的图象可知f（x1）＋f（x2）2＜f（x1＋x22），故D正确.故选BCD.
3.函数f（x）＝ax－1＋2（a＞0，且a≠1）的图象恒过定点 （1，3） .
4.已知函数f（x）＝ax＋b（a＞0，且a≠1）的定义域和值域都是[－1，0]，则a＋b＝－32.
学生用书P031
命题点1 幂函数的图象与性质
例1 （1）[2023山西省运城市景胜中学模拟]如图所示的曲线是幂函数y＝xn在第一象限内的图象.已知n分别取±2，±12四个值，与曲线C1，C2，C3，C4对应的n依次为（ A ）
A.2，12，－12，－2B.2，12，－2，－12
C.－12，－2，2，12D.－2，－12，12，2
解析 如图所示，作直线x＝2分别与曲线C1，C2，C3，C4相交，因为函数y＝2x为增函数，所以22＞212＞2－12＞2－2，所以交点由上到下对应的n值分别为2，12，－12，－2，由图可知，曲线C1，C2，C3，C4对应的n值分别为2，12，
－12，－2.故选A.
（2）[全国卷Ⅲ]已知a＝243，b＝425，c＝2513，则（ A ）
A.b＜a＜cB.a＜b＜c
C.b＜c＜aD.c＜a＜b
解析 因为a＝243＝1613，b＝425＝1615，c＝2513，且幂函数y＝x13在R上单调递增，指数函数y＝16x在R上单调递增，所以b＜a＜c.故选A.
方法技巧
1.对于幂函数的图象识别问题，解题关键是把握幂函数的性质，尤其是单调性、奇偶性、图象经过的定点等.
2.比较幂值大小的方法
（1）同底不同指的幂值大小比较：利用指数函数的单调性进行比较.
（2）同指不同底的幂值大小比较：利用幂函数的单调性进行比较.
（3）既不同底又不同指的幂值大小比较：常找到一个中间值，通过比较幂值与中间值的大小来判断.
训练1 （1）[2024陕西省汉中市名校联考]已知幂函数f（x）＝（m2＋m－1）xm的图象与坐标轴没有公共点，则f（2）＝（ A ）
A.12B.2C.2D.22
解析 因为f（x）为幂函数，所以m2＋m－1＝1，解得m＝－2或m＝1，又f（x）的图象与坐标轴无公共点，故m＜0，所以m＝－2，故f（x）＝x－2，所以f（2）＝（2）-2＝12.故选A.
（2）若（2m＋1）12＞（m2＋m－1）12，则实数m的取值范围是 [5－12，2） .
解析 因为函数y＝x12的定义域为[0，＋∞），且在定义域内单调递增，所以2m+1≥0，m2＋m－1≥0，2m+1>m2＋m－1，解得5－12≤m＜2，所以实数m的取值范围为[5－12，2）.
命题点2 指数幂的运算
例2 计算：
（1）（－338）－23＋（0.002）－12－10×（5－2）－1＋（2－3）0＝ －1679 ；
解析 原式＝（－1）－23×（338）－23＋（1500）－12－105－2＋1＝（278）－23＋50012－10×（5＋2）＋1＝49＋105－105－20＋1＝－1679.
（2）若x12＋x－12＝3，则 x32＋x－32－3x2＋x－2－2＝ 13 .
解析 由x12＋x－12＝3，两边平方，得x＋x－1＝7，
∴x2＋x－2＝47，∴x2＋x－2－2＝45.
由（x12＋x－12）3＝33，得x32＋3x12＋3x－12＋x－32＝27.
∴x32＋x－32＝18，∴x32＋x－32－3＝15.
∴x32＋x－32－3x2＋x－2－2＝13.
方法技巧
指数幂的运算技巧
训练2 （1）[2024重庆八中模拟]已知10α＝2－12，10β＝3213，则1034β＋12α＝ 2 .
解析 1034β＋12α＝（10β）34×（10α）12＝（3213）34×（2－12）12＝25×13×34＋（－12）×12＝2.
（2）a3b23ab2（a14b12）4a－13b13＝ ab （a＞0，b＞0）.
解析 原式＝（a3b2a13b23）12ab2a－13b13＝a32＋16－1+13·b1+13－2－13＝ab.
命题点3 指数函数的图象及应用
例3 （1）已知函数y＝kx＋a的图象如图所示，则函数y＝ax＋k的图象可能是（ B ）
AB C D
解析 由函数y＝kx＋a的图象可得k＜0，0＜a＜1.函数y＝ax＋k的图象可以看作是把y＝ax的图象向右平移－k个单位长度得到的，且函数y＝ax＋k是减函数，故此函数的图象与y轴交点的纵坐标大于1，结合所给的选项，可知选B.
（2）[2024上海奉贤致远高级中学模拟]已知a∈R，若关于x的方程｜3x－1｜－2a＝0有两个不相等的实根，则a的取值范围是 （0，12） .
解析 关于x的方程｜3x－1｜－2a＝0有两个不相等的实根，即曲线y＝
｜3x－1｜与直线y＝2a的图象有两个交点，作出y＝｜3x－1｜与y＝2a的图象，如图，易得a的取值范围是（0，12）.
命题拓展
已知a∈R，若关于x的方程｜ax－1｜－2a＝0有两个不等的实根，则a的取值范围是 （0，12） .
解析 关于x的方程｜ax－1｜－2a＝0有两个不等的实根，即曲线y＝｜ax－1｜与直线y＝2a的图象有两个交点，y＝｜ax－1｜的图象是由y＝ax的图象先向下平移1个单位长度，再将x轴下方的图象沿x轴翻折到x轴上方得到的.当a＞1时，如图1，两图象只有一个交点，不合题意；当0＜a＜1时，如图2，要使两个函数图象有两个公共点，则0＜2a＜1，得0＜a＜12.
图1图2
综上可知，a的取值范围是（0，12）.
方法技巧
与指数函数有关的图象问题的求解策略
注意 在指数函数图象变换时，注意特殊点（如定点）、特殊线（如渐近线）的变化.
训练3 [2024重庆市巴蜀中学适应性考试]已知函数f（x）＝ax－1－2（a＞0，且a≠1）的图象恒过定点M（m，n），则函数g（x）＝m＋xn的图象不经过（ D ）
A.第一象限B.第二象限
C.第三象限D.第四象限
解析 ∵a0＝1，∴f（x）＝ax－1－2的图象恒过定点（1，－1），∴m＝1，n＝－1，
∴g（x）＝1＋1x，其图象不经过第四象限，故选D.
命题点4 指数函数的性质及应用
角度1 比较大小
例4 （1）[2023天津高考]若a＝1.010.5，b＝1.010.6，c＝0.60.5，则a，b，c的大小关系为（ D ）
A.c＞a＞bB.c＞b＞a
C.a＞b＞cD.b＞a＞c
解析 因为函数f（x）＝1.01x是增函数，且0.6＞0.5＞0，所以1.010.6＞1.010.5＞1，即b＞a＞1；因为函数g（x）＝0.6x是减函数，且0.5＞0，所以0.60.5＜0.60＝1，即c＜1.综上，b＞a＞c.故选D.
（2）[2023全国卷甲]已知函数f（x）＝e－（x－1）2.记a＝f（22），b＝f（32），c＝
f（62），则（ A ）
A.b＞c＞aB.b＞a＞c
C.c＞b＞aD.c＞a＞b
解析 f（x）＝e－（x－1）2是由函数y＝eu和u＝－（x－1）2复合而成的函数，y＝eu为R上的增函数，u＝－（x－1）2在（－∞，1）上单调递增，在（1，＋∞）上单调递减，由复合函数的单调性可知，f（x）在（－∞，1）上单调递增，在（1，＋∞）上单调递减.易知
f（x）的图象关于直线x＝1对称，所以c＝f（62）＝f（2－62），又22＜2－62＜32＜1，所以f（22）＜f（2－62）＜f（32），所以b＞c＞a，故选A.
方法技巧
比较指数幂大小的常用方法
角度2 解简单的指数方程或不等式
例5 [2024北京市十一学校模拟]若不等式3ax－1＜（13）ax2恒成立，则实数a的取值范围是（ B ）
A.（－4，0）B.（－4，0]
C.（0，4）D.[0，4）
解析 因为不等式3ax－1＜（13）ax2恒成立，即3ax－1＜3－ax2恒成立，所以ax－1＜－ax2恒成立，即ax2＋ax－1＜0恒成立，
当a＝0时，－1＜0恒成立，符合题意；
当a≠0时，则a