福建省泉州市惠安县惠东五校2024-2025学年九年级上学期期中考试数学试题

这是一份福建省泉州市惠安县惠东五校2024-2025学年九年级上学期期中考试数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1.下列二次根式是最简二次根式的是（ ）
A. B. C. D.
2.下列计算正确的是（ ）
A. B.
C. D.
3.已知是关于的一元二次方程的一个解，则的值为（ ）
A. B. C.1 D.2
4.如图，，直线与这三条平行线分别交于点和点，若，则的长为（ ）
A. B.2 C. D.3
5.用配方法解方程，下列配方结果正确的是（ ）
A. B.
C. D.
6.某商品经过连续两次降价，销售单价由原来200元降到160元，设平均每次降价的百分率为，根据题意可列方程为（ ）
A. B.
C. D.
7.如图，已知与是以点为位似中心的位似图形，位似比为，下列说法错误的是（ ）
A. B.
C. D.
8.如图，在正方形中，，点为上一点，连接交于点，延长交的延长线于点，若，则的长为（ ）
A. B. C.4 D.
9.化简的结果为（ ）
A. B. C. D.
10.如图，在直角梯形中，，点为边上一动点，若与是相似三角形，则满足条件的点的个数是（ ）
A.1个 B.2个 C.3个 D.4个
二、填空题：本题共6小题，每小题4分，共24分．
11.若二次根式在实数范围内有意义，则的取值范围是__________．
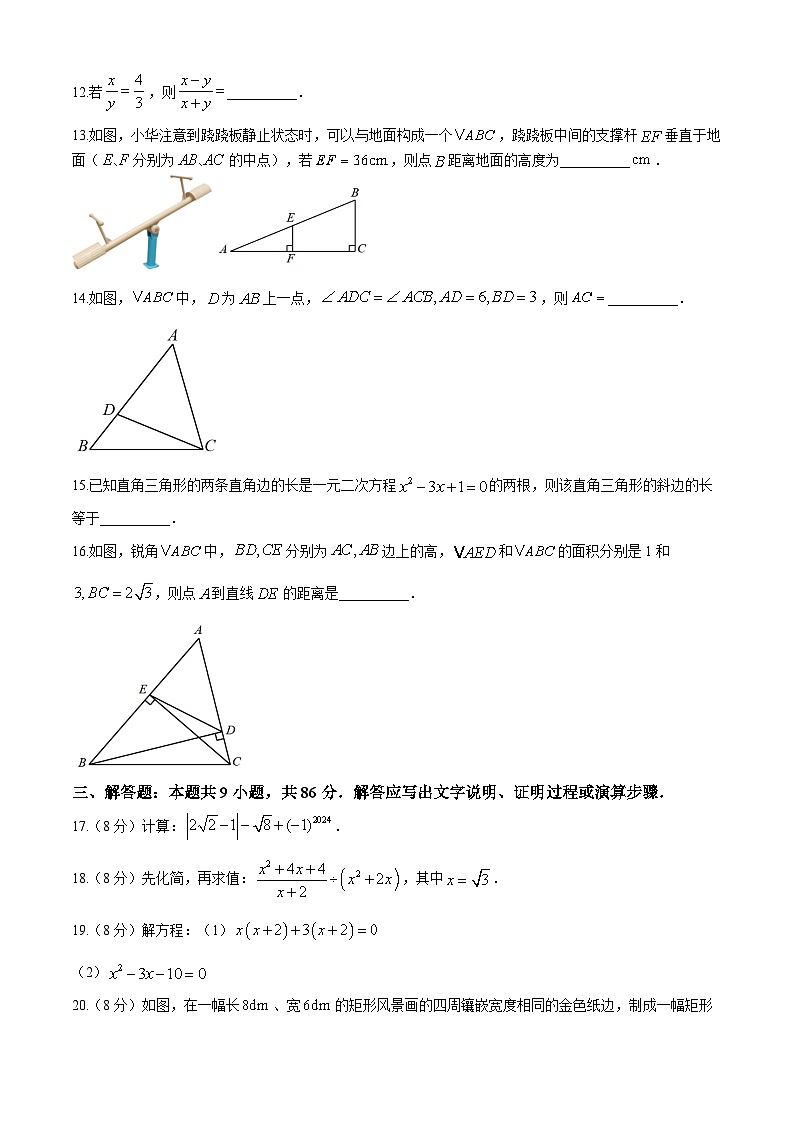
12.若，则__________．
13.如图，小华注意到跷跷板静止状态时，可以与地面构成一个，跷跷板中间的支撑杆垂直于地面（分别为的中点），若，则点距离地面的高度为__________．
14.如图，中，为上一点，，则__________．
15.已知直角三角形的两条直角边的长是一元二次方程的两根，则该直角三角形的斜边的长等于__________．
16.如图，锐角中，分别为边上的高，和的面积分别是1和，则点到直线的距离是__________．
三、解答题：本题共9小题，共86分．解答应写出文字说明、证明过程或演算步骤．
17.（8分）计算：．
18.（8分）先化简，再求值：，其中．
19.（8分）解方程：（1）
（2）
20.（8分）如图，在一幅长、宽的矩形风景画的四周镶嵌宽度相同的金色纸边，制成一幅矩形挂图，已知整个挂图的面积是，求金色纸边的宽是多少．
21.（8分）如图，在中，是斜边上的高．
（1）求证：；
（2）若，求的长．
22.（10分）已知关于的一元二次方程．
（1）求证：该方程总有两个实数根；
（2）若该方程有两个不相等的正整数解，求整数的值．
23.（10分）根据以下销售情况，解决销售任务．
24.（13分）如图，是等腰三角形，，点分别在上，且．
（1）求证：；
（2）若，求的长；
（3）探究：长是否存在最小值，若存在，请求出该最小值；若不存在，请说明理由．
25.（13分）如图，，且与分别交于．
（1）如图（1），当三点共线时，求的值；
（2）当由图（1）位置，绕点逆时针旋转．
①如图（2），当时，求的值；
②如图（3），当时，求的值．
2024年秋季期中质量监测
初三年级数学学科参考答案
一、选择题：本题共10小题，每小题4分，共40分．
1.B 2.D 3.B 4.A 5.C
6.A 7.D 8.B 9.A 10.A
二、填空题：本题共6小题，每小题4分，共24分．
11. 12. 13.72 14. 15. 16.1
三、解答题：本题共9小题，共86分．
17.（8分）
解：原式
18.（8分）
解：原式
当时，
原式
19.（8分）
解：（1）原方程化为：
即或
（2）原方程化为：
即或
20.（8分）
解：设金色纸边的宽是
依题意，得
即
解得（不合舍去）
答：金色纸边的宽是．
21.（8分）
证明：（1）
，即
即
又
（2）由（1）知
即
即
22.（10分）
解：（1）
法一：原方程化为
解得
即该方程有两个实数根
法二：
该方程总有两个实数根
（2）原方程化为
解得
方程有两个不相等的正整数解
时，符合题意
时，不合题意，舍去
整数
23.（10分）
解：任务1：甲店每天的销售量件，乙店每天的销售量件
任务2：甲每天盈利为：元
当时，原式
乙每天盈利为：元
当时，原式
任务3：设两家分店下降的价格均为元
依题意，得
即
解得
答：每件衬衫下降11元
24.（13分）
解：（1）
又
即
又
（2）
法一：由（1）知
即
即
法二：过点作，交于点
又
（3）设
由（1）知
即
法一：方程有解，即
，得
即最大值为
最小值为
法二：
即最大值为
最小值为
法三：由
为定值
当最小时，最小
则最小时，
由勾股定理求出最小值为
最小值为
25.（13分）
解：（1）
，即
．
又
（2）①
又
即
则
即
②法一：连结
又，即
又
又
则
即
又
．
法二：
由比例的性质得（此处，若在解答题中，此性质结论是否要证明？）
即销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，它们的销售情况如下：
店面
甲店
乙店
日销售情况
每天可售出20件，每件盈利40元．
每天可售出32件，每件盈利30元．
市场调查
经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件．
情况设置
设甲店每件祄衫降价元，乙店每件衬衫降价元．
任务解决
任务1
甲店每天的销售量__________件（用含的代数式表示）．
乙店每天的销售量__________件（用含的代数式表示）．
任务2
当时，分别求出甲、乙店每天的盈利．
任务3
总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和为2244元．