江苏无锡市东林中学2024-2025学年七上数学第11周阶段性训练模拟练习【含答案】

这是一份江苏无锡市东林中学2024-2025学年七上数学第11周阶段性训练模拟练习【含答案】，共16页。试卷主要包含了在中，无理数共有等内容，欢迎下载使用。
1．甲、乙两人给一片花园浇水，甲单独做需要4小时完成浇水任务，乙单独做需要6小时完成浇水任务．现由甲、乙两人合作，完成浇水任务需要（ ）
A．2.4小时B．3.2小时C．5小时D．10小时
2．如图，数轴上点A、B、C、D所表示的数分别是a、b、c、d，若abcd＜0，ab＞cd，则原点的位置在（ ）
A．点A的左边B．线段AB上C．线段BC上D．线段CD上
3．在中，无理数共有（ ）
A．1个B．2个C．3个D．4个
4．如图，数轴的单位长度为1，如果点A表示的数是﹣1，那么点B表示的数是（ ）
A．0B．1C．2D．3
5．把一个两位数的十位上的数与个位上的数交换位置，所得的新两位数比原数大9，则符合条件的两位数的个数是（ ）
A．7B．8C．9D．10
6．某商品原价a元，按下列两种方案调整价格，方案一：先涨价10%，再降价10%；方案二：先涨价20%，再降价20%．下列关于售价的说法正确的是（ ）
A．方案一售价更高B．方案二售价更高
C．两种方案售价相同D．不确定
7．幻方是古老的数字问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条斜对角线上的3个数之和相等．如图是一个未完成的幻方，则m与n的差是（ ）
A．6B．7C．8D．9
8．在下列给出的四个多项式中，为三次二项式的多项式是（ ）
A．a2﹣3B．a3+2ab﹣1C．4a3﹣bD．4a2﹣3b+2
9．某学校七年级进行一次徒步活动，带队教师和学生们以4km/h的速度从学校出发，20min后，小王骑自行车前去追赶．如果小王以12km/h的速度行驶，那么小王要用多少小时才能追上队伍？设小王要用xh才能追上队伍，那么可列出的方程是（ ）
A．12x＝4（x+20）B．12x＝4（+x）
C．12x＝4×+xD．4x＝12（x）
10．有理数a，b，c在数轴上的对应点的位置如图所示，则下列结论正确的是（ ）
A．a﹣b＜0B．a+c＜0C．|b|＜|a|D．bc＜0
11．A种饮料比B种饮料单价少1元，小峰买了2瓶A种饮料和3瓶B种饮料，一共花了13元，如果设A种饮料单价为x元/瓶，那么下面所列方程正确的是（ ）
A．2（x﹣1）+3x＝13B．2（x+1）+3x＝13
C．2x+3（x+1）＝13D．2x+3（x﹣1）＝13
12．已知点A、B、C在同一条直线上，线段AB＝5，BC＝3，则线段AC的长度是（ ）
A．8B．2
C．8或2D．以上都不对
13．某年的某个月份中有5个星期三，它们的日期之和为80（把日期作为一个数，例如把22日看作22），那么这个月的3号是星期（ ）
A．日B．一C．二D．四
二．填空题（共4小题）
14．若方程ax+b＝3的解是x＝5，则关于x的方程a（x+1）+b＝3的解是 ．
15．若|x|＝2，y2＝25，且|x+y|≠x+y，则x﹣y的值是 ．
16．已知M＝2a2﹣ab+b﹣1，M﹣3N＝a2+3ab+2b+1．若计算M﹣[2N﹣（M﹣N）]的结果与字母b无关，则a的值是 ．
17．若|m﹣1|+|n+3|＝0，则m的相反数是 ，n的倒数是 ．
三．解答题（共7小题）
18．商店购进一批衬衫，每件衬衫的进价为40元，将每件衬衫提高20%的价格出售，当这批衬衫还剩下50件时，已收回这批衬衫的全部成本，还赚了400元．这批衬衫共购进多少件？
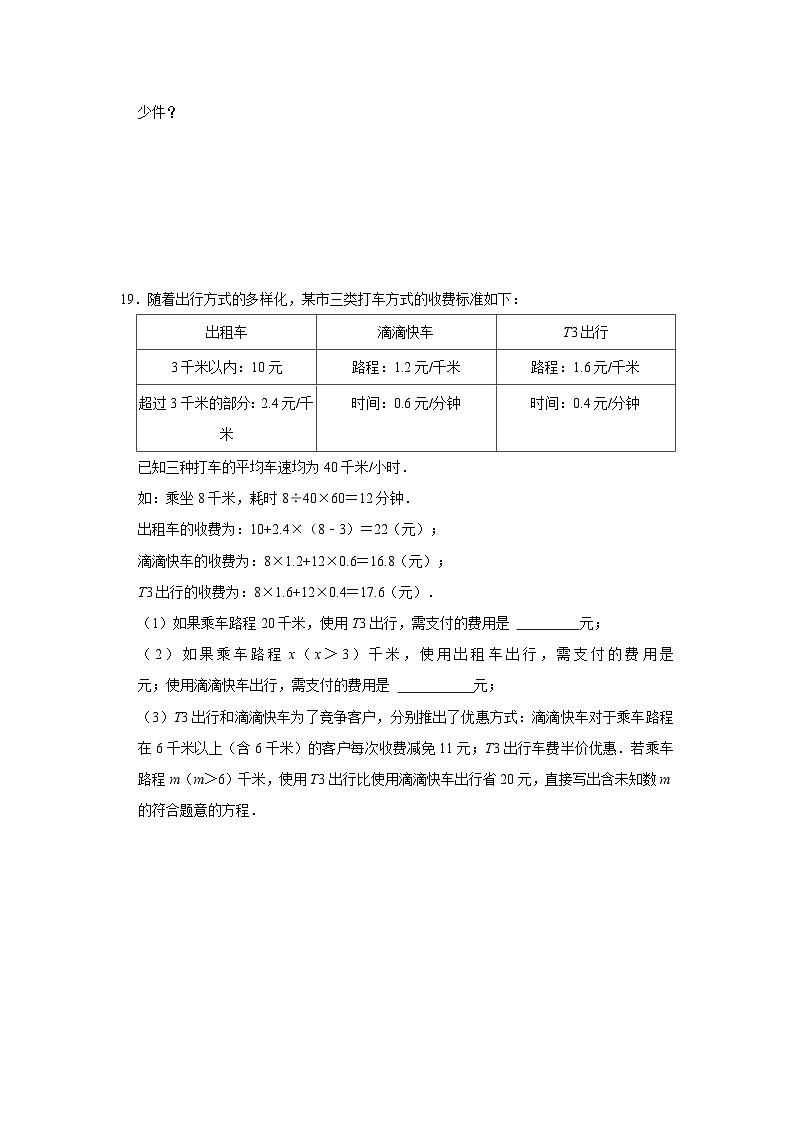
19．随着出行方式的多样化，某市三类打车方式的收费标准如下：
已知三种打车的平均车速均为40千米/小时．
如：乘坐8千米，耗时8÷40×60＝12分钟．
出租车的收费为：10+2.4×（8﹣3）＝22（元）；
滴滴快车的收费为：8×1.2+12×0.6＝16.8（元）；
T3出行的收费为：8×1.6+12×0.4＝17.6（元）．
（1）如果乘车路程20千米，使用T3出行，需支付的费用是 元；
（2）如果乘车路程x（x＞3）千米，使用出租车出行，需支付的费用是 元；使用滴滴快车出行，需支付的费用是 元；
（3）T3出行和滴滴快车为了竞争客户，分别推出了优惠方式：滴滴快车对于乘车路程在6千米以上（含6千米）的客户每次收费减免11元；T3出行车费半价优惠．若乘车路程m（m＞6）千米，使用T3出行比使用滴滴快车出行省20元，直接写出含未知数m的符合题意的方程．
20．观察下面有规律排列的三行数：
（1）第一行数中，第7个数是 ，第8个数是 ．
（2）观察第二行、第三行数与第一行数的关系，解决下列问题：
①第二行数中，第7个数是 ，第三行数中，第7个数是 ；
②取每行数的第2022个数，计算这三个数的和是 ；
③如图，在第二行、第三行数中，用两个长方形组成“阶梯形”方框，框住4个数，左右移动“阶梯形”方框，是否存在框住的4个数的和为﹣5118，若存在，求这四个数中最左边的数，若不存在，请说明理由．
④取每行数的第n个数，这3个数中最大的数记为a，最小的数记为b，若3a+2b＝2052，直接写出n的值．
21．点A，B在数轴上分别表示有理数a，b，且（a+36）2+|b+20|＝0．我们将A，B两点间的距离记为AB．
（1）a＝ ，b＝ ，AB＝ ；
（2）若点C在数轴上，且AC+BC＝35，求点C表示的有理数；
（3）M，P，Q三点在数轴上，点O为原点，点M表示的数为12．P，Q两点分别从A，B两点同时出发，沿数轴的正方向运动，在到达点O前，P，Q两点的运动速度分别为4个单位长度/秒和2个单位长度/秒，点P经过点O后的速度变为原速度的一半，点Q经过点O后的速度变为原速度的2倍．设运动时间为t秒，当OP＝QM时，求t的值．
22．如图所示，在一条不完整的数轴上从左到右有点A、B、C，其中点A到点B的距离为3，点B到点C的距离为8，设点A、B、C所对应的数的和是m．
（1）若以A为原点，则数轴上点B所表示的数是 ；若以B为原点，则m＝ ；
（2）若原点O在图中数轴上，且点B到原点O的距离为4，求m的值．
23．如图，已知A、B两地相距6千米，甲骑自行车从A地出发前往C地，同时乙从B地出发步行前往C地．
（1）已知甲的速度为16千米/小时，乙的速度为4千米小时，求两人出发几小时后甲追上乙？
（2）甲追上乙后，两人都提高了速度，但甲比乙每小时仍然多行12千米，甲到达C地后立即返回，两人在B、C两地的中点处相遇，此时离甲追上乙又经过了2小时，求A、C两地相距多少千米？
24．如图，在数轴上点A所表示的数是﹣5，点B在点A的右侧，AB＝6；点C在AB之间，AC＝2BC．
（1）在数轴上描出点B；
（2）求点C所表示的数，并在数轴上描出点C；
（3）已知在数轴上存在点P，使PA+PC＝PB，求点P所表示的数．
参考答案与试题解析
一．选择题（共13小题）
1．【解答】解：设完成浇水任务需要x小时，依题意有
（+）x＝1，
解得x＝2.4．
故完成浇水任务需要2.4小时．
故选：A．
2．【解答】解：∵abcd＜0，
∴要么a＜0，b、c、d＞0，要么a，b，c＜0，d＞0，
又∵ab＞cd，
∴a，b，c＜0，d＞0，
∴原点的位置在线段CD上．
故选：D．
3．【解答】解：∵﹣，3.5，1.3是有理数，
π，0.1010010001…是无理数，
故选：B．
4．【解答】解：∵数轴的单位长度为1，如果点A表示的数是﹣1，
∴点B表示的数是：3．
故选：D．
5．【解答】解：设这个两位数个位上的数为x，十位上的数为y，
根据题意得10x+y﹣（x+10y）＝9，
整理得y＝x﹣1，
∴或或或或或或或，
∴这个两位数是12或23或34或45或56或67或78或89，
符合条件的两位数的个数是8，
故选：B．
6．【解答】解：方案一：（1+10%）（1﹣10%）a＝0.99a（元）．
方案二：（1+20%）（1﹣20%）a＝0.96a（元）．
∵0.99a＞0.96a，
∴两种方案的销售价格不一样，方案一售价更高．
故选：A．
7．【解答】解：设左上角的数为z，右上角的数为x，正中间的数为y，
根据题意得x+21+m＝4+7+m，
解得x＝﹣10，
∴﹣10+y+4＝﹣10+21+m，
∴y＝m+17，
∴n+m+17+21＝4+7+m，
解得n＝﹣27，
∴4﹣27+z＝m+m+17+z，
解得m＝﹣20，
∴m﹣n＝﹣20﹣（﹣27）＝7，
故选：B．
8．【解答】解：A选项是二次二项式，故该选项不符合题意；
B选项是三次三项式，故该选项不符合题意；
C选项是三次二项式，故该选项符合题意；
D选项是二次三项式，故该选项不符合题意；
故选：C．
9．【解答】解：∵小王比队伍晚出发h（20min），且小王要用xh才能追上队伍，
∴小王追上队伍时，队伍出发了（+x）h．
依题意得：12x＝4（+x）．
故选：B．
10．【解答】解：利用数轴，可以判断出a＞b，则a﹣b＞0，故A选项不符合题意；
由数轴可以看出c＜0＜a，|c|＞|a|，则a+c＜0，故B选项符合题意；
由数轴可以看出|b|＞|a|，故C选项不符合题意；
由数轴可以看出c＜0，b＜0，则bc＞0，故D选项不符合题意．
故选：B．
11．【解答】解：设A种饮料单价为x元/瓶，则B种饮料单价为（x+1）元，
根据小峰买了2瓶A种饮料和3瓶B种饮料，一共花了13元，
可得方程为：2x+3（x+1）＝13．
故选：C．
12．【解答】解：①当点C在线段AB上时，
由线段的和差，得AC＝AB﹣BC＝5﹣3＝2，
②当点C在线段AB的延长线上，
由线段的和差，得AC＝AB+BC＝5+3＝8．
综上所述：AC的长为2或8．
故选：C．
13．【解答】解：设第一个星期三为x号，
依题意得：x+x+7+x+14+x+21+x+28＝80
解得x＝2，即这个月第一个星期三是2号，
因此3号是星期四．
故选：D．
二．填空题（共4小题）
14．【解答】解：把x＝5代入方程ax+b＝3得：5a+b＝3，
所以3﹣b＝5a，
∵a（x+1）+b＝3，
∴ax+a+b＝3，
∴ax＝3﹣b﹣a，
∴ax＝5a﹣a，
∴ax＝4a，
∵a≠0，
∴x＝4．
故答案为：x＝4．
15．【解答】解：∵|x|＝2，y2＝25，
∴x＝±2，y＝±5，
∵|x+y|≠x+y，
∴x+y＜0，
∴x＝2，y＝﹣5或x＝﹣2，y＝﹣5，
当x＝2，y＝﹣5时，x﹣y＝2﹣（﹣5）＝7，
当x＝﹣2，y＝﹣5时，x﹣y＝﹣2﹣（﹣5）＝3．
故答案为：7或3．
16．【解答】解：原式＝M﹣（2N﹣M+N）
＝M﹣2N+M﹣N
＝2M﹣3N，
∵M＝2a2﹣ab+b﹣1，M﹣3N＝a2+3ab+2b+1，
∴原式＝M+M﹣3N
＝2a2﹣ab+b﹣1+a2+3ab+2b+1
＝3a2+2ab+3b，
＝3a2+（2a+3）b，
∵计算M﹣[2N﹣（M﹣N）]的结果与字母b无关，
∴2a+3＝0，
∴a＝﹣．
故答案为：﹣．
17．【解答】解：由题意得，m﹣1＝0，n+3＝0，
解得，m＝1，n＝﹣3，
则m的相反数是﹣1，n的倒数是﹣．
故答案为：﹣1，﹣．
三．解答题（共7小题）
18．【解答】解：设批衬衫共购进x件，
由题意可得商品售价为40×（1+20%）＝48（元），
所以（x﹣50）×48＝40x+400，
解得：x＝350．
答：这批衬衫共购进350件．
19．【解答】解：（1）由题意得：20÷40×60＝30（分钟），
则T3出行的打车费为：1.6×20+0.4×30＝32+12＝44（元）．
故答案为：44；
（2）根据题意，
乘车路程x（x＞3）千米，
使用出租车出行，需支付的费用是：10+2.4×（x﹣3）＝（2.4x+2.8）元，
使用滴滴快车出行，需支付的费用是：1.2x+（×60）×0.6＝2.1x 元．
故答案为：（2.4x+2.8）；2.1x；
（3）设打车的路程为m（m＞6）千米，依题意得：
T3出行的收费为：W1＝0.5×（1.6m+×60×0.4）＝1.1m 元，
滴滴快车的收费为：W2＝1.2m+×60×0.6﹣11＝（2.1m﹣11）元，
根据题意，可得，2.1m﹣11﹣1.1m＝20，
m＝31．
20．【解答】解：（1）因为（﹣2）7＝﹣128，（﹣2）8＝256，
故答案为：﹣128，256；
（2）①因为﹣128﹣1＝﹣129，﹣129×（﹣2）＝258，
故答案为：﹣129，258；
②因为（﹣2）2022+[（﹣2022）2﹣1]+（﹣2）•[（﹣2022）2﹣1]＝1，
故答案为：1；
③设最左边的数为x﹣1，则其第二个数为：（﹣2x﹣1）第三行第一个数为：﹣2（﹣2x﹣1）＝4x+2，第二个数为：﹣2（4x﹣1）＝﹣8x+2，
∴（x﹣1）+（﹣2x﹣1）+（4x+2）+（﹣8x+2）＝﹣5118，
∴x＝1024，
∴x﹣1＝1023，
答：这四个数中最左边的数是1023；
④从上到下，设这三个数为：（﹣2）n＝x、（﹣2）n﹣1＝﹣x﹣1、（﹣2）n+1+2＝﹣2x+2，
当x＞0时，
3x+2（﹣2x+2）＝2052，
x＝﹣2048舍去），
当x＜0时，
3（﹣2x+2）+2（x﹣1）＝2052，
∴x＝﹣512，
∴（﹣2）n＝﹣512，
∴n＝9，
综上所述；n＝9．
21．【解答】解：（1）∵（a+36）2+|b+20|＝0．而（a+36）2，≥0，|b+20|≥0．
∴a+36＝0，b+20＝0，
解得a＝﹣36，b＝﹣20，
AB＝|﹣36﹣（﹣20）|＝16，
故答案为：﹣36，﹣20，16；
（2）设点C在数轴上所表示的数为x，
由于AB＝16，而AC+BC＝35，因此点C不可能在线段AB上，
①当点C在BA的延长线上时，
∵AC+BC＝35，
∴﹣36﹣x﹣20﹣x＝35，
解得x＝﹣，
②当点C在AB的延长线上时，
∵AC+BC＝35，
∴x+36+x+20＝35，
解得x＝﹣，
所以点C在数轴上所表示的数为﹣或﹣；
（3）①当点P、Q都在原点的左侧时，
OP＝|﹣36+4t|＝36﹣4t，MQ＝|﹣20+2t|+12＝20﹣2t+12＝32﹣2t，
所以36﹣4t＝32﹣2t，
解得t＝2；
②由于点P到达原点需要36÷4＝9秒，而点Q到达原点需要20÷2＝10秒，
当点P、Q在原点的右侧，在点M的左侧时，
OP＝2（t﹣9）＝2t﹣18，OQ＝4（t﹣10）＝4t﹣40，MQ＝12﹣4t+40＝52﹣4t，
由于OP＝MQ，
所以2t﹣18＝52﹣4t，
解得t＝；
当点P、Q都在点M的右侧时，
OP＝2（t﹣9）＝2t﹣18，OQ＝4（t﹣10）＝4t﹣40，MQ＝4t﹣40﹣12＝4t﹣52，
由于OP＝MQ，
所以2t﹣18＝4t﹣52，
解得t＝17；
综上所述，当OP＝QM时，t的值为2或或17．
22．【解答】解：（1）∵点A到点B的距离为3，A为原点，
∴数轴上点B所表示的数是3，B为原点，
∴数轴上点B所表示的数是0，点A表示的数是﹣3，点C表示的数是8，
∴m＝﹣3+0+8＝5，
故答案为：3，5；
（2）∵点A到点B的距离为3，点B到点C的距离为8，点B到原点O的距离为4，
∴当O在B的左边时，A、B、C三点在数轴上所对应的数分别为1、4、12，
∴m＝1+4+12＝17，
当O在B的右边时，A、B、C三点在数轴上所对应的数分别为﹣7、﹣4、4，
∴m＝﹣7﹣4+4＝﹣7，
综上所述：m的值为﹣7或17．
23．【解答】解：（1）设两人出发t小时后甲追上乙，根据题意得
16t﹣4t＝6，
得t＝
答：两人出发小时后甲追上乙．
（2）设两个人的速度提高了a千米/小时，BC段长度为x千米，根据题意有
2（16+a）﹣2（4+a）＝x
得x＝24
故BC段距离为24千米
∴AC＝AB+BC＝6+24＝30
答：A、C两地相距30千米．
24．【解答】解：（1）点B在数轴上的位置如图1所示．
（2）解法一：因为AC＝2BC，点C在AB之间，
所以AB＝AC+BC＝3BC．
因为AB＝1﹣（﹣5）＝6，
所以BC＝2．
因为点B所表示的数是1，
1﹣2＝﹣1
所以点C所表示的数是﹣1．
解法二：设BC＝x，则AC＝2x．
因为AB＝1﹣（﹣5）＝6，
所以x+2x＝6．
解得x＝2．
因为点B所表示的数是1，
1﹣2＝﹣1，
所以点C所表示的数是﹣1．
解法三：设点C所表示的数为x．
因为点C在AB之间，
所以BC＝1﹣x，AC＝x﹣（﹣5）＝x+5．
因为AC＝2BC，
所以x+5＝2（1﹣x）．
解得x＝﹣1，
点C在数轴上的位置，如图2所示．
（3）解法一：因为PA+PC＝PB，
所以点P在点C左侧．
因为点A表示的数是﹣5，点B表示的数是1，点C表示的数是﹣1，
所以AC＝﹣1﹣（﹣5）＝4，AB＝1﹣（﹣5）＝6．
①当点P在AC之间时，
设PA＝x，则PC＝AC﹣PA＝4﹣x．
所以PB＝PC+BC＝4﹣x+2＝6﹣x．
因为PA+PC＝PB，
所以x+4﹣x＝6﹣x．
解得 x＝2．
因为点A所表示的数是﹣5，﹣5+2＝﹣3，
此时点P所表示的数是﹣3．
②当点P在点A左侧时，
设PA＝x，则PC＝PA+AC＝4+x，PB＝PA+AB＝x+6，
因为PA+PC＝PB，
所以x+4+x＝6+x．
解得 x＝2．
因为点A所表示的数是﹣5，﹣5﹣2＝﹣7，
此时点P所表示的数是﹣7．
所以点P所表示的数是﹣3或﹣7．
解法二：因为PA+PC＝PB，
所以点P在点C左侧．
所以PA＝PB﹣PC＝BC＝2．
因为点A所表示的数是﹣5，
所以点P所表示的数是﹣3或﹣7．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/11/14 17:50:06出租车
滴滴快车
T3出行
3千米以内：10元
路程：1.2元/千米
路程：1.6元/千米
超过3千米的部分：2.4元/千米
时间：0.6元/分钟
时间：0.4元/分钟