2024-2025学年江苏省连云港市海州区新海实验中学八年级（上）期中数学试卷（含答案）

这是一份2024-2025学年江苏省连云港市海州区新海实验中学八年级（上）期中数学试卷（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.以下是清华大学、北京大学、上海交通大学、中国人民大学四个大学的校徽，其中是轴对称图形的是( )
A. B. C. D.
2.下列四组线段中，可以构成直角三角形的是( )
A. 3cm、4cm、5cmB. 2cm、3cm、6cm
C. 2cm、3cm、4cmD. 4cm、5cm、6cm
3.如图，图中的两个三角形是全等三角形，其中一些角和边的大小如图所示，那么x的值是( )
A. 30°B. 36°C. 65°D. 79°
4.如图，在△ABC中，AB=AC，AC的垂直平分线l交BC于点D.若∠DAC=37°，则∠B的度数是( )
A. 37°B. 30°C. 28°D. 26°
5.下列说法错误的是( )
A. 有一个内角是60°的等腰三角形是等边三角形
B. 角平分线上的点到角两边的距离相等
C. 等腰三角形的角平分线、中线、高线三线合一
D. 轴对称图形中，对应点的连线被对称轴垂直平分
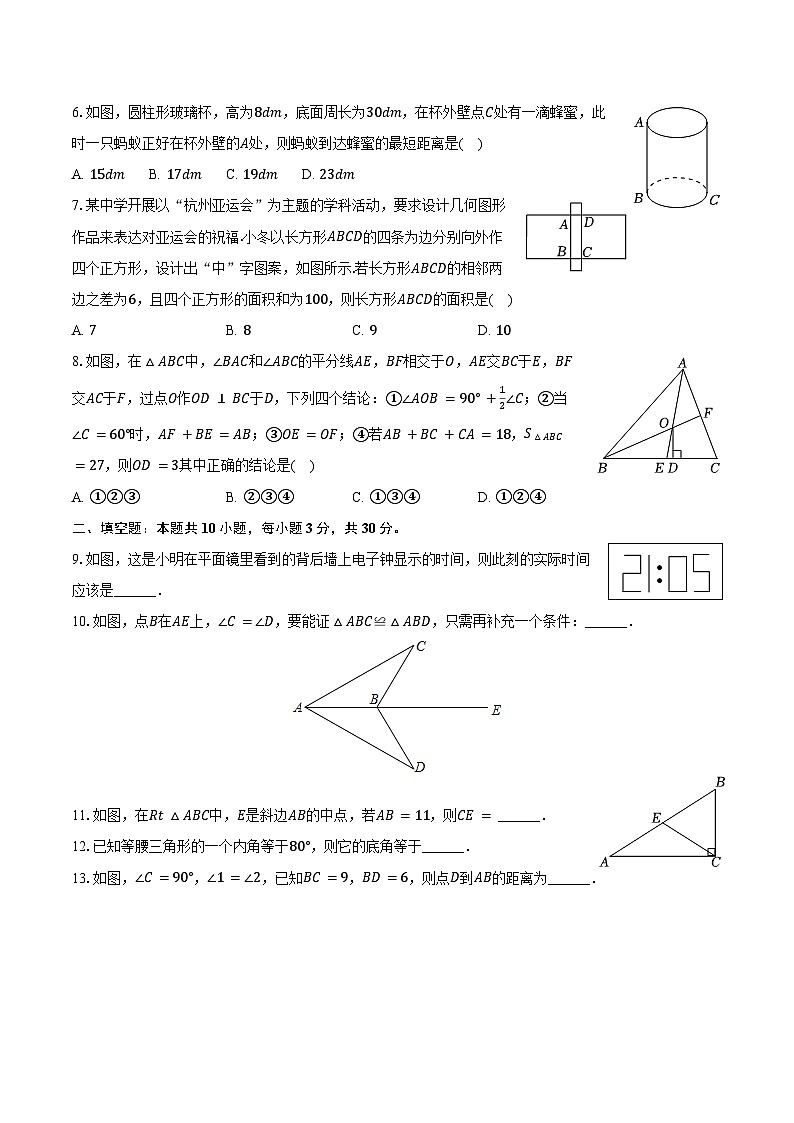
6.如图，圆柱形玻璃杯，高为8dm，底面周长为30dm，在杯外壁点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁的A处，则蚂蚁到达蜂蜜的最短距离是( )
A. 15dm B. 17dm C. 19dm D. 23dm
7.某中学开展以“杭州亚运会”为主题的学科活动，要求设计几何图形作品来表达对亚运会的祝福.小冬以长方形ABCD的四条为边分别向外作四个正方形，设计出“中”字图案，如图所示.若长方形ABCD的相邻两边之差为6，且四个正方形的面积和为100，则长方形ABCD的面积是( )
A. 7B. 8C. 9D. 10
8.如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，下列四个结论：①∠AOB=90°+12∠C；②当∠C=60°时，AF+BE=AB；③OE=OF；④若AB+BC+CA=18，S△ABC=27，则OD=3其中正确的结论是( )
A. ①②③B. ②③④C. ①③④D. ①②④
二、填空题：本题共10小题，每小题3分，共30分。
9.如图，这是小明在平面镜里看到的背后墙上电子钟显示的时间，则此刻的实际时间应该是______．
10.如图，点B在AE上，∠C=∠D，要能证△ABC≌△ABD，只需再补充一个条件：______．
11.如图，在Rt△ABC中，E是斜边AB的中点，若AB=11，则CE= ______．
12.已知等腰三角形的一个内角等于80°，则它的底角等于______．
13.如图，∠C=90°，∠1=∠2，已知BC=9，BD=6，则点D到AB的距离为______．
14.如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠P+∠Q= ______度.
15.如图，直线m是△ABC中BC边的垂直平分线，点P是直线m上的一动点.若AB=7，
AC=5，则△APC周长的最小值是______．
16.如图，在△ABC中，AB=AC，AB>BC，点D在边BC上，CD=2BD，点E，F在线段AD上，∠1=∠2=∠BAC，若△BDE的面积为2，△ABC的面积为21，则△CFD的面积为______．
17.如图，门上钉子P处挂着一个“欢迎光临”的长方形挂牌ABCD，测得AB=5dm，AD=12dm.(如图1)，当挂牌水平悬挂(即BC与地面平行)时，测得挂绳AP=DP−10dm，将该门挂的挂绳长度缩短2dm后重新挂上，此时不小心把挂牌弄斜了(如图2)，发现AC与地面平行，且点P、D、C三点在同一直线上，则点B的高度下降了______dm．
18.如图，在Rt△ABC中，∠ACB=90°，点D是AB的中点，连接DC，作DE⊥DC交AC于点E.
若AB=10，CE=6，则AE的长为______．
三、解答题：本题共8小题，共96分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题12分)
如图，∠A=∠D，BF=EC，AC//DF；求证：AB=DE．
20.(本小题12分)
如图1，荡秋千是中国古代北方少数民族创造的一种运动.有一天，小明在公园里游玩，如图2，他发现秋千静止时，踏板离地的垂直高度DE=1m，将它往前推送6m(水平距离BC=6m)时，秋千的踏板离地的垂直高度BF=CE=3m，秋千的绳索始终拉得很直，求绳索AD的长度？
21.(本小题12分)
如图所示的网格由边长为1个单位长度的小正方形组成，点A、B、C在小正方形的顶点上．
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C．
(2)作∠ABC的平分线交AC于D．
(3)BC2的值为______．
(4)与△ABC全等且有1个公共顶点C的格点三角形有______个(△ABC除外)．
22.(本小题12分)
如图，在△ABC中，AB=AC，CD是∠ACB的平分线，DE//BC，交AC于点E，且∠CDE=25°．
(1)求证：△CDE是等腰三角形；
(2)求∠A的度数．
23.(本小题12分)
在△ABC中，AB−=c，BC=a，AC=b.如图1，若∠C=90°时，根据勾股定理有a2+b2=c2．

(1)如图2，当△ABC为锐角三角形时，类比勾股定理，判断a2+b2与c2的大小关系，并证明；
(2)如图3，当△ABC为钝角三角形时，类比勾股定理，判断a2+b2与c2的大小关系，并证明；
(3)如图4，一块四边形的试验田ABCD，已知∠ADC=90°，AD=80米，CD=60米，AB=260米，BC=240米，求这块试验田的面积．
24.(本小题12分)
如图，在△ABC中，∠BAC=90°，AB=AC，点D是BC上一动点，连接AD，过点A作AE⊥AD，并且始终保持AE=AD，连接CE．
(1)求证：△ABD≌△ACE；
(2)若AF平分∠DAE交BC于F，BD=2，FC=3.求DF2的值．
25.(本小题12分)
如图1，△ABC中，CD⊥AB于D，且BD：AD：CD=2：3：4，
(1)试说明△ABC是等腰三角形；
(2)已知S△ABC=40cm2，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t(秒)，
①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．
26.(本小题12分)
如图①，等腰△ABC中，AB=AC，点D是AC上一动点，点E、P分别在BD延长线上，且AB=AE，CP=EP．
【问题思考】在图①中，求证：∠BPC=∠BAC；
【问题再探】若∠BAC=60°，如图②，探究线段AP、BP、EP之间的数量关系，并证明你的结论；
【问题拓展】若∠BAC=90°且BD平分∠ABC，如图③，若BD=5，则PC的值为______．
参考答案
1.B
2.A
3.C
4.A
5.C
6.B
7.A
8.D
9.20：15
10.∠CAB=∠DAB(答案不唯一)
11.112
12.80°或50°
13.3
14.45
15.12
16.9
17.1113
18.73
19.证明：∵AC/​/DF，
∴∠ACB=∠DFE，
∵BF=EC，
∴BF+FC=EC+CF，
即BC=EF，
在△ABC和△DEF中，
∠A=∠D∠ACB=∠DFEBC=EF，
∴△ABC≌△DEF(AAS)，
∴AB=DE．
20.解：由题意得：∠ACB=90°，
在Rt△ACB中，由勾股定理得：AC2+BC2=AB2，
设绳索AD的长度为x m，则AC=(x−2)m，
∴x2=62+(x−2)2，
解得：x=10，
答：绳索AD的长度是10m．
21.
（3）20
（4） 5
22.(1)证明：∵CD是∠ACB的平分线，
∴∠DCB=∠ECD，
又∵DE//BC，
∴∠DCB=∠EDC，
∴∠ECD=∠EDC，
∴EC=ED，
∴△CDE是等腰三角形；
(2)解：∵∠CDE=25°，
∴∠ECD=∠DCB=25°
∴∠ACB=50°，
∵AB=AC，
∴∠B=∠ACB=50°，
∴∠A=180°−2∠B=80°．
23.解：(1)猜想：a2+b2>c2，证明如下：
如图2，过点A作AD⊥BC于点D，
设CD=x，则BD=a−x，
在Rt△ACD中，由勾股定理得：b2−x2=AD2，
在Rt△ABD中，由勾股定理得：c2−(a−x)2=AD2，
∴b2−x2=c2−(a−x)2，
∴b2+a2=c2+2ax，
∵a，b，c，x均为正数，
∴b2+a2>c2；
(2)猜想：b2+a2