陕西省西安市西安理工大学附属中学2024-2025学年九年级上学期期中考试数学试题

这是一份陕西省西安市西安理工大学附属中学2024-2025学年九年级上学期期中考试数学试题，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
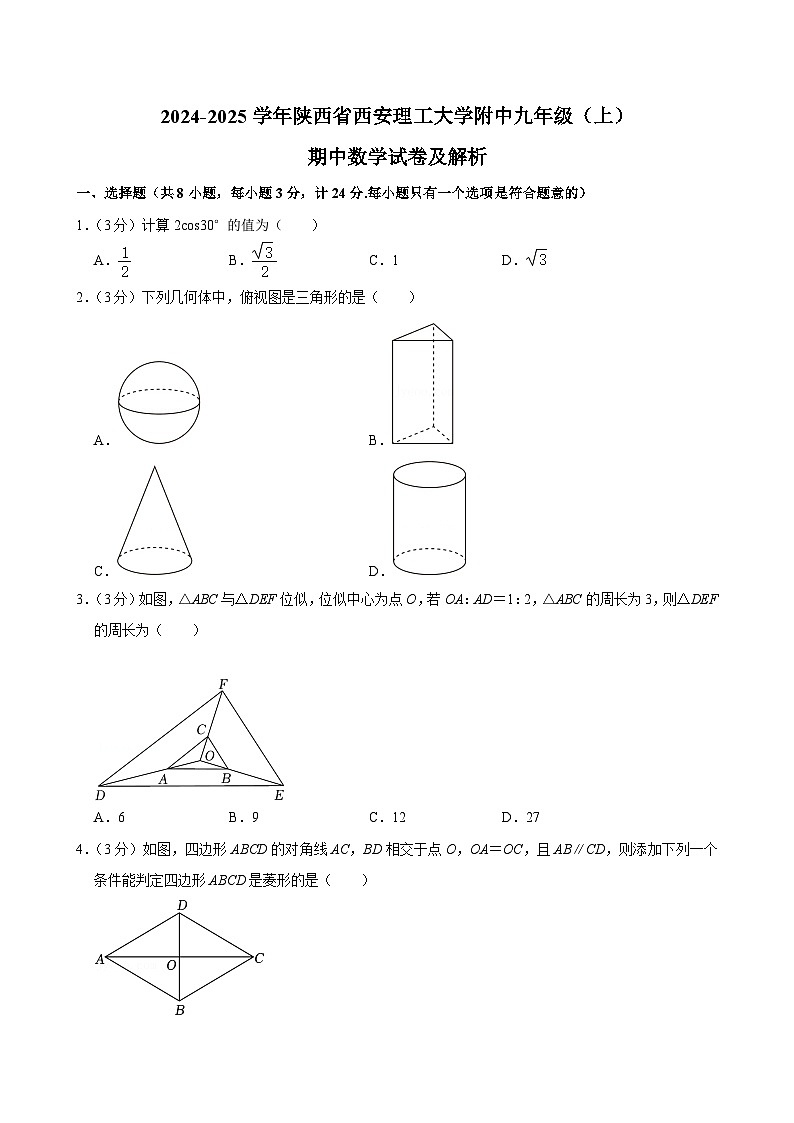
一、选择题（共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的）
1．（3分）计算2cs30°的值为（ ）
A．B．C．1D．
2．（3分）下列几何体中，俯视图是三角形的是（ ）
A．B．
C．D．
3．（3分）如图，△ABC与△DEF位似，位似中心为点O，若OA：AD＝1：2，△ABC的周长为3，则△DEF的周长为（ ）
A．6B．9C．12D．27
4．（3分）如图，四边形ABCD的对角线AC，BD相交于点O，OA＝OC，且AB∥CD，则添加下列一个条件能判定四边形ABCD是菱形的是（ ）
A．AC＝BDB．∠ADB＝∠CDBC．∠ABC＝∠DCBD．AD＝BC
5．（3分）已知关于x的一元二次方程x2+2x﹣1＝0，对该方程的根的判断，正确的是（ ）
A．有两个不相等的实数根
B．有两个相等的实数根
C．没有实数根
D．无法判断
6．（3分）如图，反比例函数的图象与经过原点的直线l相交于A、B两点，点A坐标为（﹣2，1），那么B点的坐标为（ ）
A．（﹣2，1）B．（2，1）C．（1，﹣2）D．（2，﹣1）
7．（3分）如图，矩形ABCD的边长AB＝3，AD＝6，点F在线段BC上，且BF：FC＝1：2，AF与DB交于点N，则AN＝（ ）
A．B．C．D．
8．（3分）已知x＝﹣1是关于x的方程2x2+ax﹣5＝0的一个根，且点A（﹣1，y1），B（﹣2，y2）都在反比例函数的图象上，则y1和y2满足（ ）
A．y1＞y2＞0B．y2＜y1＜0C．y2＞y1＞0D．y1＜y2＜0
二、填空题（共5小题，每小题3分，计15分）
9．（3分）用配方法解一元二次方程x2﹣2x﹣5＝0时，将它化为（x+a）2＝b的形式，则a+b的值为 ．
10．（3分）木箱里装有仅颜色不同的12个红球和若干个蓝球，随机从木箱里摸出一个球，记下颜色后再放回，经多次的重复实验，发现摸到红球的频率稳定在0.6附近，则估计木箱中蓝球有 个．
11．（3分）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若AD＝4，tan∠DAC＝，则BC的长为 ．
12．（3分）如图，在△AOB中，AB⊥x轴于点B，∠AOB＝30°，OA＝4，反比例函数的图象经过点A，则k的值为 ．
13．（3分）如图，在正方形ABCD中，AB＝2，点E，F分别为BC，CD边上的动点，连接AE，BF交于点G，连接DG，点M，N分别为CD，DG的中点，连接MN．若AE＝BF，则MN的最小值为 ．
三、解答题（共13小题，计81分.解答应写出过程）
14．（5分）解方程：6x2﹣5x﹣1＝0．
15．（5分）计算：cs245°﹣tan60°tan30°+|sin60°﹣1|．
16．（5分）装卸工人往一辆大型运货车上装载货物，装完货物所需时间y（min）与装载速度x（t/min）之间的函数关系如图：
（1）求y与x之间的函数关系式；
（2）如果以1.5t/min的速度装货，需要多长时间才能装完货物？
17．（5分）如图，在△ABC中，∠B＝2∠A，利用尺规作图法在边AC上求作一点D，使得△BDC∽△ABC．（不写作法，保留作图痕迹）
18．（5分）如图，点E，G在△ABC的边AB，AC上，连接EG，点D为△ABC外一点，连接AD，CD，点F在AD上，连接GF，EG∥BC，GF∥DC，AE＝3，EB＝2，AF＝6，求AD的值．
19．（5分）如图是同一副扑克牌中的两张牌“黑桃Q”和“黑桃K”，现在把这两张牌从中间剪断，分成如图的4张背面形状相同的半张牌，并背面向上混合在一起搅匀．小撤和小尼做游戏，小撤先从这4张半张牌中随机地抽取一张（不放回），小尼接着再随机地抽取一张．
（1）小撒抽到半张“黑桃Q”的概率是 ；
（2）游戏规定：所抽取的两张中，能拼成一张完整的扑克牌，那么小撒获胜；否则小尼获胜，你认为这个游戏公平吗？并请用列表法或画树状图法说明理由．
20．（5分）如图，在△ABC中，∠ACB＝90°，O是AB的中点，CO＝6.5，BC＝5．
（1）求AC的长；
（2）求cs∠OCA与tan∠B的值．
21．（6分）如图，在正方形ABCD中，点E、F分别在CD、AD上，连接AE，BF相交于点G，AE⊥BF．
（1）求证：∠AED＝∠FBC；
（2）连接BE，BF，若AE＝4，求四边形ABEF的面积．
22．（7分）“靠山吃山，靠水吃水”，金丝峡景区的人民依靠制作手工艺品也走出了一条致富路，其经营模式一般为生产组的产品由商店代理销售．已知某商店代理销售“竹编篮”平均每天可销售50套，每套盈利22元，在每套降价幅度不超过6元的情况下，每下降1元，则每天可多售4套．如果每天要盈利1160元，每套应降价多少元？
23．（7分）阳光明媚的一天，小明与同学计划测量学校周围一栋古建筑AB的高度，由于古建筑底部不可到达，他们在古建筑AB的影子顶端C处，直立一个长为2米的标杆DC，经测量，同一时刻标杆的影子CE＝1米，接下来他们沿着BE方向从E点出发走了9米到达点F处（即EF＝9米），利用无人机测得GF＝12米，并用无人机在G处测得B点的俯角为37°，AB⊥BF，DC⊥BF，GF⊥BF，点B、C、E、F在一条直线上，求古建筑AB的高．（参考数据：sin37°≈，cs37°≈
24．（8分）如图，在▱ABCD中，对角线AC、BD相交于点O，E为AO上一点，BF⊥BD交DE的延长线于点F，且EF＝DE．
（1）求证：四边形ABCD是菱形；
（2）DF交线段AB于点G，若OD2＝OE•OA，求证：△AGE∽△DBF．
25．（8分）如图，已知正比例函数的图象与反比例函数的图象相交于点A（3，n）和点B；
（1）求n和k的值；
（2）以AO为边作菱形AOCD，使点C在x轴正半轴上，点D在第一象限，线段CD交反比例函数第一象限的图象于点E，连接AE、OE，求△AOE的面积；
（3）在（2）的条件下，点P是反比例函数图象上的点，若S△COP＝2S△AOE，求点P的坐标．
26．（10分）【问题探究】
（1）如图1，在▱ABCD中，连接AC，∠BAD＝∠ABC．
①求证：▱ABCD是矩形；
②若∠ACB＝30°，探究线段BC与线段AB之间的数量关系．
【问题解决】
（2）如图2所示，矩形ABCD是一块待开发的旅游景点规划地，CA，CE，CF是从入口C通往三个观光点A，E，F的路线，其中CE＝CF，且∠ECF＝∠ACB＝30°，因自然地理环境的限制，观光点A无法直接到达观光点E，F，为方便旅客顺利、便捷地从观光点A到达观光点E，F（观光点E，F分别在AB，AD上），现要在AE，AF上架一座桥梁，已知AC＝4km，桥梁AE的造价为200万元/km，桥梁AF的造价为100万元/km，求建好AE和AF两座桥梁所需要的总造价．
2024-2025学年陕西省西安理工大学附中九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的）
1．（3分）计算2cs30°的值为（ ）
A．B．C．1D．
【分析】直接把cs30°＝代入进行计算即可．
【解答】解：原式＝2×
＝．
故选：D．
【点评】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．
2．（3分）下列几何体中，俯视图是三角形的是（ ）
A．B．
C．D．
【分析】根据常见简单几何体的三视图，可得答案．
【解答】解：A．球的俯视图是圆，故本选项不符合题意；
B．该三棱柱的俯视图是三角形，故本选项符合题意；
C．该圆锥的俯视图是带圆心的圆，故本选项不符合题意；
D．该圆柱的俯视图是圆，故本选项不符合题意．
故选：B．
【点评】本题考查了简单几何体的三视图，熟记简单几何体的三视图是解题关键．
3．（3分）如图，△ABC与△DEF位似，位似中心为点O，若OA：AD＝1：2，△ABC的周长为3，则△DEF的周长为（ ）
A．6B．9C．12D．27
【分析】利用位似的性质得△ABC∽△DEF，AC：DF＝OA：OD＝1：3，然后根据相似三角形的性质解决问题．
【解答】解：∵△ABC与△DEF位似，点O为位似中心．OA：AD＝1：2，
∴△ABC∽△DEF，AC：DF＝OA：OD＝1：3，
∴△ABC的周长：△DEF的周长＝1：3，
∴△DEF的周长为3×3＝9．
故选：B．
【点评】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．位似图形必须是相似形，对应点的连线都经过同一点；对应边平行或共线．
4．（3分）如图，四边形ABCD的对角线AC，BD相交于点O，OA＝OC，且AB∥CD，则添加下列一个条件能判定四边形ABCD是菱形的是（ ）
A．AC＝BDB．∠ADB＝∠CDBC．∠ABC＝∠DCBD．AD＝BC
【分析】根据菱形的判定方法分别对各个选项进行判定，即可得出结论．
【解答】解：∵AB∥CD，
∴∠BAO＝∠DCO，∠ABO＝∠CDO，
∵OA＝OC，
∴△AOB≌△COD（AAS），
∴AB＝CD，
∴四边形ABCD是平行四边形，
A、当AC＝BD时，四边形ABCD是矩形；故选项A不符合题意；
B、∵AB∥CD，
∴∠ABD＝∠CDB，
∵∠ADB＝∠CDB，
∴∠ADB＝∠ABD，
∴AD＝AB，
∴四边形ABCD为菱形，故选项B符合题意；
C、∵AB∥CD，
∴∠ABC+∠BCD＝180°，
∵∠ABC＝∠DCB
∴∠ABC＝∠DCB＝90°，
∴四边形ABCD是矩形；故选项C不符合题意；
D、当AD＝BC时，不能判定四边形ABCD为菱形；故选项D不符合题意．
故选：B．
【点评】本题考查了菱形的判定，平行四边形的判定和性质，等腰三角形的判定和性质，熟练掌握菱形的判定定理是解题的关键．
5．（3分）已知关于x的一元二次方程x2+2x﹣1＝0，对该方程的根的判断，正确的是（ ）
A．有两个不相等的实数根
B．有两个相等的实数根
C．没有实数根
D．无法判断
【分析】根据Δ＝b2﹣4ac与0的关系直接求解即可得到答案．
【解答】解：由题意可得：
Δ＝22﹣4×1×（﹣1）＝8＞0，
∴该方程有两个不相等的实数根，
故选：A．
【点评】本题考查一元二次方程根的判别式，熟练掌握根的判别式是解题的关键．
6．（3分）如图，反比例函数的图象与经过原点的直线l相交于A、B两点，点A坐标为（﹣2，1），那么B点的坐标为（ ）
A．（﹣2，1）B．（2，1）C．（1，﹣2）D．（2，﹣1）
【分析】反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称．
【解答】解：∵点A（﹣2，1）与B关于原点对称，
∴B点的坐标为（2，﹣1）．
故选：D．
【点评】本题主要考查了反比例函数图象的中心对称性，要求同学们要熟练掌握．
7．（3分）如图，矩形ABCD的边长AB＝3，AD＝6，点F在线段BC上，且BF：FC＝1：2，AF与DB交于点N，则AN＝（ ）
A．B．C．D．
【分析】根据勾股定理求出AF，结合矩形性质得到BF∥AD，BC＝AD，△BFN∽△DAN即可解答．
【解答】解：∵四边形ABCD是矩形，
∴BF∥AD，BC＝AD，∠ABC＝90°，
∵BF：FC＝1：2，AD＝6，
∴BF＝×6＝2，
∵BF∥AD，
∴△BFN∽△DAN，
∴＝＝，
∴AN＝AF，
∵∠ABC＝90°，AB＝3，AF＝2，
∴AF＝＝，
∴AN＝．
故选：B．
【点评】本题考查矩形性质，勾股定理，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题关键．
8．（3分）已知x＝﹣1是关于x的方程2x2+ax﹣5＝0的一个根，且点A（﹣1，y1），B（﹣2，y2）都在反比例函数的图象上，则y1和y2满足（ ）
A．y1＞y2＞0B．y2＜y1＜0C．y2＞y1＞0D．y1＜y2＜0
【分析】先利用方程的解求得a的值，即可判断反比例函数的图象所在的象限，然后利用反比例函数的性质解决问题即可．
【解答】解：∵x＝﹣1是关于x的方程2x2+ax﹣5＝0的一个根，
∴2×（﹣1）2﹣a﹣5＝0，
∴a＝﹣3，
∴a＜0，
∴反比例函数的图象在二、四象限，在每个象限y随x的增大而增大，
∵点A（﹣1，y1），B（﹣2，y2）都在反比例函数的图象上，
∴点A（﹣1，y1），B（﹣2，y2）都在第二象限，
∵x1＞x2，
∴y1＞y2＞0，
故选：A．
【点评】本题考查一元二次方程的解，反比例函数的图象上的点的坐标特征，解题的关键是熟练掌握反比例函数的性质．
二、填空题（共5小题，每小题3分，计15分）
9．（3分）用配方法解一元二次方程x2﹣2x﹣5＝0时，将它化为（x+a）2＝b的形式，则a+b的值为 5 ．
【分析】根据配方法的步骤：①把常数项移到等号的右边；②等式两边同时加上一次项系数一半的平方，把左边配成一个完全平方式，右边化为一个常数项，由此可得出a，b的值，即可得出答案．
【解答】解：∵x2﹣2x﹣5＝0，
∴x2﹣2x＝5，
∴x2﹣2x+1＝5+1，
∴（x﹣1）2＝6，
∴a＝﹣1，b＝6，
∴a+b＝5，
故答案为：5．
【点评】本题考查解一元二次方程﹣配方法，能够将一元二次方程正确配方是解答本题的关键．
10．（3分）木箱里装有仅颜色不同的12个红球和若干个蓝球，随机从木箱里摸出一个球，记下颜色后再放回，经多次的重复实验，发现摸到红球的频率稳定在0.6附近，则估计木箱中蓝球有 8 个．
【分析】设袋子中蓝球有x个，根据概率公式列出算式，再进行计算即可得出答案．
【解答】解：设袋子中蓝球有x个，根据题意得：
＝0.6，
解得：x＝8，
经检验x＝8是原方程的解，
估计袋子中蓝球有8个；
故答案为：8．
【点评】本题利用了用大量试验得到的频率可以估计事件的概率．关键是根据摸到红球的频率得到相应的等量关系．
11．（3分）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若AD＝4，tan∠DAC＝，则BC的长为 4 ．
【分析】解直角三角形求得CD＝2，再利用三线合一即可求解．
【解答】解：∵AD⊥BC，，
∴，
∵AD＝4，
∴CD＝2，
AB＝AC，AD⊥BC，
∴BC＝2CD＝4．
故答案为：4．
【点评】此题考查了解直角三角形、等腰三角形的性质，解直角三角形求出CD＝2是解题的关键．
12．（3分）如图，在△AOB中，AB⊥x轴于点B，∠AOB＝30°，OA＝4，反比例函数的图象经过点A，则k的值为 ﹣4 ．
【分析】先求出点A的坐标，再代入计算即可得．
【解答】解：∵AB⊥x轴于点B，∠AOB＝30°，OA＝4，
∴，，
∴，
将点代入反比例函数得：，
故答案为：．
【点评】本题考查了求反比例函数的解析式等知识，熟练掌握待定系数法是解题关键．
13．（3分）如图，在正方形ABCD中，AB＝2，点E，F分别为BC，CD边上的动点，连接AE，BF交于点G，连接DG，点M，N分别为CD，DG的中点，连接MN．若AE＝BF，则MN的最小值为 ．
【分析】首先证明Rt△ABE≌△Rt△BCF（HL），然后利用全等三角形性质得到∠AGB＝90°，从而确定G在G在以AB为直径的圆上，接着利用中位线的性质即可确定MN最小的求解方法．
【解答】解：∵四边形ABCD为正方形，
∴AB＝BC，∠ABE＝∠BCF＝90°，
在Rt△ABE和△Rt△BCF中，
，
∴Rt△ABE≌△Rt△BCF（HL），
∴∠BAE＝CBF，而∠CBF+∠ABG＝90°，
∴∠BAG+∠ABG＝90°，
∴∠AGB＝90°，
∴G在以AB为直径的圆上，O为圆心，
而点M，N分别为CD，DG的中点，
∴MN＝CG，值．
∴当MN最小，那么CG最小，
若CG最小，则O、G、C三点共线，
∵AB＝2，
∴BO＝1，BC＝2，
∴OC＝，
最小CG＝OC﹣OG＝﹣1．
∴MN的最小值．
故答案为：．
【点评】本题主要考查了正方形的性质，也利用了全等三角形的性质和三角形的中位线的性质，同时也利用了勾股定理解进行计算，综合性比较强．
三、解答题（共13小题，计81分.解答应写出过程）
14．（5分）解方程：6x2﹣5x﹣1＝0．
【分析】本题利用因式分解法即可求解．
【解答】解：原方程左侧因式分解得：（6x+1）（x﹣1）＝0，
6x+1＝0或x﹣1＝0，
解得：．
【点评】本题考查了解一元二次方程，熟练掌握直接开平方法，因式分解法，配方法和公式法是解题的关键．
15．（5分）计算：cs245°﹣tan60°tan30°+|sin60°﹣1|．
【分析】把特殊角的三角函数值代入进行计算，即可解答．
【解答】解：cs245°﹣tan60°tan30°+|sin60°﹣1|
＝（）2﹣×+|﹣1|
＝﹣1+1﹣
＝．
【点评】本题考查了实数的运算，特殊角的三角函数值，准确熟练地进行计算是解题的关键．
16．（5分）装卸工人往一辆大型运货车上装载货物，装完货物所需时间y（min）与装载速度x（t/min）之间的函数关系如图：
（1）求y与x之间的函数关系式；
（2）如果以1.5t/min的速度装货，需要多长时间才能装完货物？
【分析】（1）求出货物质量，根据装完货物所需时间＝的关系列出函数关系式即可；
（2）利用函数关系式，把x＝1.5代入，可求卸完货物时间．
【解答】解：（1）设该运货车上装载货物的质量m＝xy，
把（0.5，40）代入得货物的质量m＝0.5×40＝20，
∴y与x之间的函数关系式；
（2）当x＝1.5时，有，
∴需要才能装完货物．
【点评】本题考查了反比例函数的应用，确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式是解题的关键．
17．（5分）如图，在△ABC中，∠B＝2∠A，利用尺规作图法在边AC上求作一点D，使得△BDC∽△ABC．（不写作法，保留作图痕迹）
【分析】作∠ABC平分线，交AC于D即可．
【解答】解：如图，作∠ABC平分线BD，点D即为所求．理由如下：
由作图可知：BD是∠ABC平分线，
∴∠ABC＝2∠CBD，
∵∠ABC＝2∠A，
∴，
∵∠C＝∠C，
∴△BDC∽△ABC．
【点评】本题考查作图﹣相似变换，掌握相似三角形的判定定理是解题的关键．
18．（5分）如图，点E，G在△ABC的边AB，AC上，连接EG，点D为△ABC外一点，连接AD，CD，点F在AD上，连接GF，EG∥BC，GF∥DC，AE＝3，EB＝2，AF＝6，求AD的值．
【分析】由EG∥BC，GF∥DC得到，，再代入数据即可求出FD＝4，继而可求AD．
【解答】解：∵EG∥BC，GF∥DC，
∴，，
∴，
∴FD＝4，
∵AF＝6，
∴AD＝AF+FD＝10．
【点评】本题考查了平行线分线段成比例定理，熟练掌握知识点是解题的关键．
19．（5分）如图是同一副扑克牌中的两张牌“黑桃Q”和“黑桃K”，现在把这两张牌从中间剪断，分成如图的4张背面形状相同的半张牌，并背面向上混合在一起搅匀．小撤和小尼做游戏，小撤先从这4张半张牌中随机地抽取一张（不放回），小尼接着再随机地抽取一张．
（1）小撒抽到半张“黑桃Q”的概率是 ；
（2）游戏规定：所抽取的两张中，能拼成一张完整的扑克牌，那么小撒获胜；否则小尼获胜，你认为这个游戏公平吗？并请用列表法或画树状图法说明理由．
【分析】（1）直直接由概率公式求解即可；
（2）画树状图，共有12种等可能的结果，其中能拼成一张完整的扑克牌的结果有4种，不能拼成一张完整的扑克牌的结果有8种，再由概率公式求出小撒获胜的概率≠小尼获胜的概率，即可得出结论．
【解答】解：（1）∵小撤从这4张半张牌中随机地抽取一张，
∴小撒抽到半张“黑桃Q”的概率是＝，
故答案为：；
（2）游戏不公平，理由如下：
设4张半张牌分别用A、a，B、b表示，
画树状图如下：
共有12种等可能的结果，其中能拼成一张完整的扑克牌的结果有4种，不能拼成一张完整的扑克牌的结果有8种，
∴小撒获胜的概率＝＝，小尼获胜的概率＝＝，
∵≠，
∴游戏不公平．
【点评】本题考查了游戏公平性以及树状图法求概率，判断游戏公平性需要先计算每个事件的概率，然后比较概率的大小，概率相等就公平，否则就不公平．用到的知识点为：概率＝所求情况数与总情况数之比．
20．（5分）如图，在△ABC中，∠ACB＝90°，O是AB的中点，CO＝6.5，BC＝5．
（1）求AC的长；
（2）求cs∠OCA与tan∠B的值．
【分析】（1）由直角三角形斜边中线的性质推出AB＝2CO＝13，由勾股定理即可求出AC＝＝12；
（2）由直角三角形斜边中线的性质推出OA＝OC，得到∠OAC＝∠OCA，因此cs∠OCA＝cs∠A＝＝，由锐角的正切即可求出tanB＝＝．
【解答】解：（1）∵∠ACB＝90°，O是AB的中点，CO＝6.5，
∴AB＝2CO＝13，
∵BC＝5，
∴AC＝＝12，
（2）∵∠ACB＝90°，O是AB的中点，
∴OC＝AB，
∴OA＝OC，
∴∠OAC＝∠OCA，
∴cs∠OCA＝cs∠A＝＝，tanB＝＝．
【点评】本题考查解直角三角形，直角三角形斜边的中线，关键是由直角三角形斜边中线的性质得到AB＝2CO＝13，OA＝OC，推出cs∠OCA＝cs∠A．
21．（6分）如图，在正方形ABCD中，点E、F分别在CD、AD上，连接AE，BF相交于点G，AE⊥BF．
（1）求证：∠AED＝∠FBC；
（2）连接BE，BF，若AE＝4，求四边形ABEF的面积．
【分析】（1）根据同角的余角相等，得到∠AFB＝∠FBC，证明△BAF≌△ADE，得到∠AFB＝∠AED，即可得出结论；
（2）分割法得到四边形ABEF的面积等于，进行计算即可．
【解答】（1）证明：∵四边形ABCD是正方形，
∴∠BAD＝∠ABC＝∠ADE＝90°，AB＝AD，
∴∠ABF+∠AFB＝∠ABF+∠FBC＝90°，
∴∠FBC＝∠AFB，
∵AE⊥BF，
∴∠ABF+∠BAG＝90°，
∵∠DAE+∠BAG＝90°，
∴∠DAE＝∠ABF，
∵∠BAD＝∠D＝90°，AB＝AD，
∴△BAF≌△ADE（ASA），
∴∠AFB＝∠AED，
∴∠AED＝∠FBC；
（2）解：∵△BAF≌△ADE，
∴BF＝AE＝4，
∵AE⊥BF，
∴四边形ABEF的面积＝．
【点评】本题考查正方形的性质，全等三角形的判定和性质，解题的关键是证明△BAF≌△ADE．
22．（7分）“靠山吃山，靠水吃水”，金丝峡景区的人民依靠制作手工艺品也走出了一条致富路，其经营模式一般为生产组的产品由商店代理销售．已知某商店代理销售“竹编篮”平均每天可销售50套，每套盈利22元，在每套降价幅度不超过6元的情况下，每下降1元，则每天可多售4套．如果每天要盈利1160元，每套应降价多少元？
【分析】设每套“竹编篮”降价x元，则每套盈利（22﹣x）元，平均每天可售出（50+4x）套，根据每天要盈利1160元，列出一元二次方程，解之取其符合题意的值即可．
【解答】解：设每套“竹编篮”降价x元，则每套盈利（22﹣x）元，平均每天可售出（50+4x）套，
由题意得：（22﹣x）（50+4x）＝1160，
整理得：2x2﹣19x+30＝0，
解得：x1＝2，x2＝7.5（不符合题意，舍去），
答：每套应降价2元．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
23．（7分）阳光明媚的一天，小明与同学计划测量学校周围一栋古建筑AB的高度，由于古建筑底部不可到达，他们在古建筑AB的影子顶端C处，直立一个长为2米的标杆DC，经测量，同一时刻标杆的影子CE＝1米，接下来他们沿着BE方向从E点出发走了9米到达点F处（即EF＝9米），利用无人机测得GF＝12米，并用无人机在G处测得B点的俯角为37°，AB⊥BF，DC⊥BF，GF⊥BF，点B、C、E、F在一条直线上，求古建筑AB的高．（参考数据：sin37°≈，cs37°≈
【分析】在Rt△BGF中利用三角函数关系求出BF，从而得到BC的长，再利用太阳光是平行光线，证明△ABC∽△DCE，利用对应边的比例关系即可求出答案．
【解答】解：由题意，知∠BGF＝90°﹣37°＝53°，
在Rt△BGF中，
GF＝12米，∠BGF＝53°，
∵tan∠BGF＝，
∴BF＝GFtan∠BGF＝12tan53°＝12×＝16（米），
∴BC＝BF﹣CE﹣EF＝16﹣1﹣9＝6（米），
∵太阳光线是平行光线，
∴AC∥DE，
∴∠ACB＝∠DEC，
∵∠ABC＝∠DCE＝90°，
∴△ABC∽△DCE，
∴，
即，
解得AB＝12米．
答：古建筑AB的高为12米．
【点评】本题考查解直角三角形的应用﹣仰角俯角问题，相似三角形的应用，平行投影，灵活运用解直角三角形和相似三角形的性质是解题的关键．
24．（8分）如图，在▱ABCD中，对角线AC、BD相交于点O，E为AO上一点，BF⊥BD交DE的延长线于点F，且EF＝DE．
（1）求证：四边形ABCD是菱形；
（2）DF交线段AB于点G，若OD2＝OE•OA，求证：△AGE∽△DBF．
【分析】（1）证明OE是△BDF的中位线，推出AC⊥BD，即可证明平行四边形ABCD是菱形；
（2）先证明△AOD∽△DOE，得到∠OAD＝∠ODE，再证明△AGE∽△DBF．
【解答】证明：（1）∵四边形ABCD是平行四边形，
∴O是BD的中点，
∵EF＝DE，即E是DF的中点，
∴OE是△BDF的中位线，
∴OE∥BF，
∵BF⊥BD，
∴OE⊥BD，即AC⊥BD，
∴平行四边形ABCD是菱形；
（2）∵OD2＝OE•OA，
∴，
又∵∠AOD＝∠DOE，
∴△AOD∽△DOE，
∴∠OAD＝∠ODE，
∵四边形ABCD是菱形，
∴∠OAD＝∠OAB，
∴∠GAE＝∠ODE
∵∠AEG＝∠DEO，
∴∠AGE＝∠DOE，
∵OE∥BF，
∴∠DBF＝∠DOE，
∴∠AGE＝∠DBF，
∴△AGE∽△DBF．
【点评】本题主要考查了菱形的性质与判定，相似三角形的性质与判定，三角形中位线定理，平行四边形的性质，熟知相似三角形的性质与判定条件是解题的关键．
25．（8分）如图，已知正比例函数的图象与反比例函数的图象相交于点A（3，n）和点B；
（1）求n和k的值；
（2）以AO为边作菱形AOCD，使点C在x轴正半轴上，点D在第一象限，线段CD交反比例函数第一象限的图象于点E，连接AE、OE，求△AOE的面积；
（3）在（2）的条件下，点P是反比例函数图象上的点，若S△COP＝2S△AOE，求点P的坐标．
【分析】（1）将点A（3，n）代入求出n的值，再将A（3，4）代入求出k的值；
（2）先根据A（3，4）求出OA，根据菱形的性质求出OC＝OA＝5，再根据S菱形AOCD＝OC•|yA|，即可求解；
（3）设点P的坐标为，根据即可求解．
【解答】解：（1）将点A（3，n）代入正比例函数，
得：，即A（3，4），
将A（3，4）代入反比例函数，
得：，
解得k＝12；
（2）∵A（3，4），
∴，
∵四边形AOCD是菱形，
∴OC＝OA＝5，
∴S菱形AOCD＝OC•|yA|＝5×4＝20，
∵点E在线段CD上，
∴；
（3）∵点P是反比例函数图象上的点，
∴设点P的坐标为，
由（2）知S△AOE＝10，
∴S△COP＝2S△AOE＝2×10＝20，
∴，
解得，
当时，，
当时，，
∴点P的坐标为或．
【点评】本题考查反比例函数与一次函数的交点问题，菱形的性质，勾股定理，三角形面积等知识点，掌握平面直线坐标系中三角形面积的求法是解题的关键．
26．（10分）【问题探究】
（1）如图1，在▱ABCD中，连接AC，∠BAD＝∠ABC．
①求证：▱ABCD是矩形；
②若∠ACB＝30°，探究线段BC与线段AB之间的数量关系．
【问题解决】
（2）如图2所示，矩形ABCD是一块待开发的旅游景点规划地，CA，CE，CF是从入口C通往三个观光点A，E，F的路线，其中CE＝CF，且∠ECF＝∠ACB＝30°，因自然地理环境的限制，观光点A无法直接到达观光点E，F，为方便旅客顺利、便捷地从观光点A到达观光点E，F（观光点E，F分别在AB，AD上），现要在AE，AF上架一座桥梁，已知AC＝4km，桥梁AE的造价为200万元/km，桥梁AF的造价为100万元/km，求建好AE和AF两座桥梁所需要的总造价．
【分析】（1）①根据有一个角是直角的平行四边形是矩形证明即可；②由∠ACB＝30°得到AC＝2AB，在Rt△ABC中，运用勾股定理即可求解；
（2）延长CB至点G，使得CG＝CA＝4，连接GE，AG，先证明△CEG≌△CFA（SAS），则GE＝AF，∠4＝∠3，则，由上知，那么，同上可得，GE＝2BE，则，此时，那么，即可求解总造价．
【解答】（1）①证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠BAD+∠ABC＝180°，
∵∠BAD＝∠ABC，
∴∠BAD＝90°，
∴四边形ABCD是矩形；
②解：；理由如下，
∵四边形ABCD是矩形，
∴∠B＝90°，
∵∠ACB＝30°，
∴AC＝2AB，
在Rt△ABC中，由勾股定理得：；
（2）解：延长CB至点G，使得CG＝CA＝4，连接GE，AG，
∵∠ECF＝∠ACB＝30°，
∴∠BCE＝∠ACF，
在△CEG和△CFA中，
，
∴△CEG≌△CFA（SAS），
∴GE＝AF，∠BGE＝∠CAF，
∵四边形ABCD是矩形，
∴AD∥BC，∠ABC＝∠ABG＝90°，
∴∠CAF＝∠ACB＝30°，
∴∠BGE＝30°，，
由上知，
∴，
在Rt△BGE中，∠BGE＝30°，
∴同上可得，GE＝2BE，
∴，
∴，
∴，
∴总造价为：（万元）．
【点评】本题考查了矩形的判定与性质，平行四边形的性质，直角三角形的性质，全等三角形的判定与性质，勾股定理，正确构造全等三角形是解题的关键。