初中数学人教版（2024）九年级上册25.3 用频率估计概率教学ppt课件

这是一份初中数学人教版（2024）九年级上册25.3 用频率估计概率教学ppt课件，共19页。PPT课件主要包含了不成活，利用频率估计概率，能用列举法求概率吗，元kg，用频率估计概率等内容，欢迎下载使用。
1. 进一步理解利用频率估计概率的方法，并能解决一些简单的实际问题；2.在解决实际问题的过程中加强对概率的认识，进一步体会利用频率的集中趋势估计概率的数学思想；3.获得解决实际问题的方法，体会利用频率估计概率的策略的作用；4.体会概率与实际生活的密切联系，调动学生学习概率知识的积极性，提高应用数学知识解决实际问题的能力.
幼苗移植会有哪些可能结果？
某林业部门要考察某种幼树在一定条件下的移植成活率，应采用什么具体做法？
两种结果可能性是否相等未知
如何利用频率去估计幼树移植的成活率呢？
实际上有的实验做起来非常麻烦，并且大量的进行这个实验也是不可能的，这就需要“模拟实验”来代替.
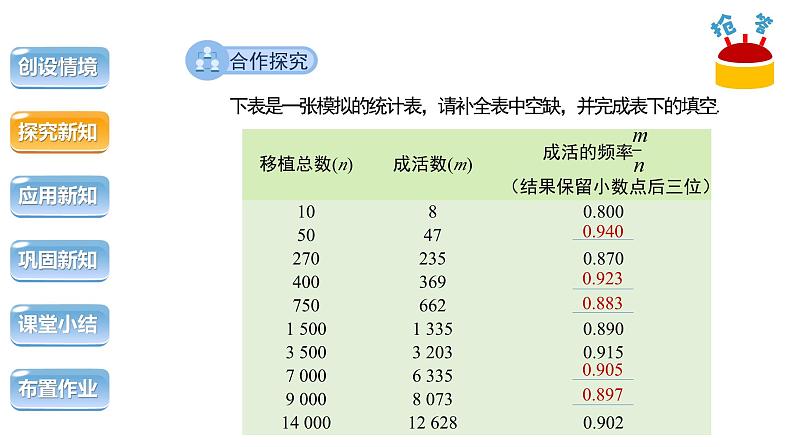
下表是一张模拟的统计表，请补全表中空缺，并完成表下的填空.
随着移植数的增加，幼树移植成活的频率越来越稳定.
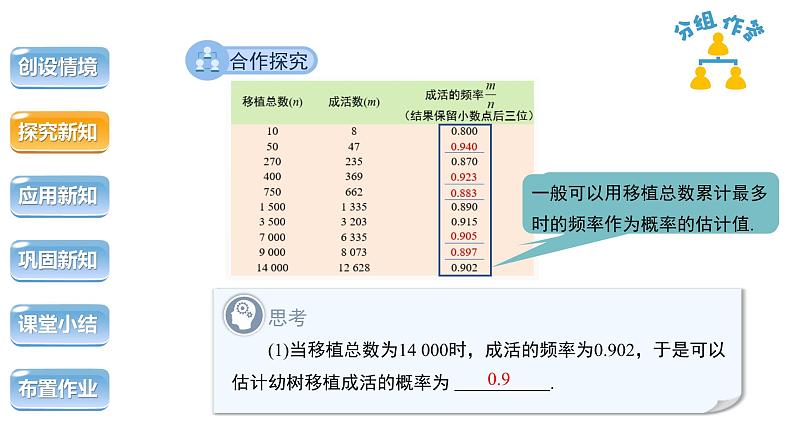
(1)当移植总数为14 000时，成活的频率为0.902，于是可以估计幼树移植成活的概率为 .
一般可以用移植总数累计最多时的频率作为概率的估计值.
(2)林业部门种植了该种幼树1 000棵，估计能成活_____棵.
成活数总数成活的概率
1 0000.9900
人们在长期的实践中发现，对于一般随机试验，在大量重复试验中，频率仍然呈现出一定的稳定性.这种在大量重复试验中反映出的客观规律，称为大数法则，亦称大数定律.
一般可以用试验次数累计最多时的频率作为概率的估计值.概率估计值小数点后保留的位数不超过频率小数点后保留的位数.
【例】某水果公司以2元/kg的成本价新进10000 kg柑橘.如果公司希望这些柑橘能够获得利润5000元，那么在出售柑橘（去掉损坏的柑橘）时，每千克大约定价为多少元比较合适？
柑橘在运输、储存中会有损坏，公司必须估算出可能损坏的柑橘总数，以便将损坏的柑橘的成本折算到没有损坏的柑橘的售价中.
销售人员首先从所有的柑橘中随机抽取若干柑橘，进行 “损坏柑橘率”的统计，并把获得的数据记录在表中.
请你帮忙完成下面的表格.
从表可以看出，随着柑橘质量的增加，柑橘损坏的频率越来越稳定.柑橘中质量为500 kg 时的损坏频率为0.103，于是可以估计柑橘损坏的概率为 (结果保留小数点后一位).由此可知，柑橘完好的概率为 .
解: 根据估计的概率可以知道，在10 000 kg 柑橘中完好柑橘的质量为 10 0000.99 000 (kg). 完好柑橘的实际成本为 设每千克柑橘的售价为 x 元，则 (x2.22)9 0005 000. 解得 x2.8 (元) 因此，出售柑橘时，每千克定价大约 2.8 元可获得利润 5 000 元.
1.大数据分析技术为打赢疫情防控阻击战发挥了重要作用．如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为2 cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为 cm2．
提示：点落入黑色部分的概率为0.6， 则黑色部分的总面积0.6正方形的面积.
2.在一个不透明的袋中装有若干个材质、大小完全相同的红球，小明在袋中放入3个黑球（每个黑球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋中红球有　 　个．
提示：摸到黑球的概率为0.15， 则0.15球的总数黑球个数.
3.某农科所在相同条件下做了某作物种子发芽率的实验，结果如下表所示：
一般地，1 000 kg种子中大约有多少是不能发芽的？
解:这批种子发芽的频率稳定在0.9，即种子发芽的概率估计为0.9，则不发芽的概率估计为0.1，
1 0000.1=100 (kg)
因此，1 000 kg种子大约有100 kg是不能发芽的.
在相同条件下，做大量重复试验，事件发生的频率会越来越稳定，我们可以把频率作为概率的估计值.
教科书第148页习题25.3第4、5题