黑龙江省牡丹江市海林市朝鲜族中学2024-2025学年高二上学期第二次月考数学试卷

这是一份黑龙江省牡丹江市海林市朝鲜族中学2024-2025学年高二上学期第二次月考数学试卷，共9页。
班： 姓名：
一、单项选择题（每小题5分 共60分）
1.抛物线的焦点坐标为（ ）
A.B.C.D.
2.直线的倾斜角是( )
A.30°B.60°C.120°D.150°
3.焦点在x轴上，长、短半轴长之和为10，焦距为，则椭圆的标准方程为
A. B. C. D.
4.设直线，的方向向量分别为，，若，则实数m等于( )
A.1B.2C.3D.4
5.不等式的解集为（ ）
A. B.C. D.
6.过点，的直线斜率为( )
A.1B.2C.3D.
7.已知是第一象限角，且，则( )
A.B.C.D.
8.已知向量与平行，则实数的值为（ ）
A．2 B．-2 C． 20 D．-20
9.已知数列的前n项和,则等于( )
A.12B.15C.18D.21
10.已知直线被圆截得的弦长为2，则( )
A.B.C.3D.4
11.已知椭圆，，分别为其左、右焦点，，B为短轴的一个端点，（O为坐标原点）的面积为，则椭圆的长轴长为( )
A.4B.8C.D.
12..已知方程表示焦点在x轴上的椭圆，则实数k的取值范围是( )
A. B.C.D.
二、填空题(每小题5分，共20分）
13.若焦点在y轴上的椭圆的离心率为,则m的值为________.
14.已知直线与直线垂直，则________.
15.曲线上的点到一个焦点的距离为12，则到另一个焦点的距离为_______.
16.按一定规律排列的数据依次为，，，，…按此规律排列，则第30个数是________.
三、解答题（17题10分，其他每小题12分，共70分）
17.求焦点坐标为、，且过点的椭圆方程。
18.已知双曲线的离心率为，求该双曲线的渐近线方程。
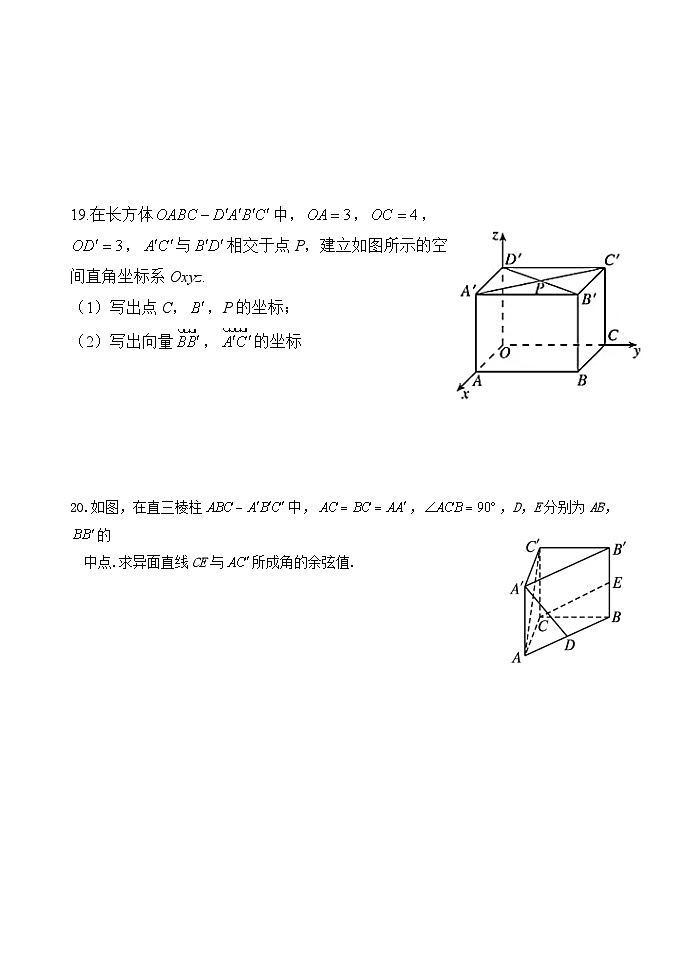
19.在长方体中，，，，与相交于点P，建立如图所示的空间直角坐标系Oxyz.
（1）写出点C，，P的坐标；
（2）写出向量，的坐标
20.如图，在直三棱柱中，，，D，E分别为AB，的
中点.求异面直线CE与所成角的余弦值.
21.如图，在多面体中，四边形是边长为2的正方形，四边形是直角梯形，其中，，且.
(1)证明：平面平面；
(2)求二面角的余弦值.
22.如图，在正方体中，,E,F分别是,的中点.
(1)求异面直线与所成角的余弦值；
(2)求点到平面的距离.
参考答案
一.CCCBCB BABABD
二.13. 14.1 15.22或2 16.答案：88901
三.
17.答案：c=4,a=6, 椭圆方程为
18.解析：根据题意，双曲线的离心率为，所以，所以，由，得，所以双曲线方程为，因此该双曲线的渐近线为.
19.答案：（1），，
（2），
解析：（1）因为，，，
所以，，.
（2）因为，
，
20.解：，
，，
，
.
异面直线CE与所成角的余弦值为.
21．答案：(1)证明见解析
(2)
解析：(1)证明：连接，因为，，，
所以，
又因为，，
所以，所以，
又因为，，
所以平面，
又因为平面，
所以平面平面.
(2)因为，
所以，
又因为，所以，
所以、、两两垂直，
建立如图所示的空间直角坐标系，各点坐标如下：
，，，，
，，，
设平面与平面的法向量分别为，，
，令，，
，令，，
设二面角的大小为，由图可知为钝角，
所以
故二面角的余弦值为
22．答案：(1)；(2)
解析：（1）以D为原点，,,所在的直线分别为x轴、y轴、z轴，
建立如图所示的空间直角坐标系，则,,,，
,，
所以直线与所成角的余弦值为；
（2）设平面的法向量为，，
则得取，则，，
得平面的一个法向量为，
所以点到平面的距离为