北师大版（2024）九年级上册第一章 特殊平行四边形2 矩形的性质与判定当堂检测题

这是一份北师大版（2024）九年级上册第一章 特殊平行四边形2 矩形的性质与判定当堂检测题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题。
1.平行四边形 ABCD 中，AC，BD 是两条对角线，如果添加一个条件，即可推出平行四边形 ABCD 是矩形，那么这个条件是
A．AB=BCB．AC=BDC．AC⊥BDD．AB⊥BD
2.在 Rt△ABC 中，已知 ∠C 为直角，斜边上的中线为 5，∠A=60∘，则 a 的值为
A． 52 B． 523 C． 5 D． 53
3.如图，在△OAB中，顶点O(0,0)，∠AOB=90°，点A在y轴的正半轴上，点B在x轴的正半轴上，OC是△OAB的中线，点C的坐标为(2,3)，将△OAB绕点O逆时针旋转，每次旋转45°，则第2021次旋转结束时，点A的坐标为( )
A. (4,-4)
B. (23,-4)
C. (32,-32)
D. (32,-3)
4．如图，小明将一张为14cm，宽为10cm的长方形（AE＞DE）纸张剪去了一个直角三角形，量得AB＝4cm，CD＝6cm，则剪去的直角三角形的斜边长为（ ）
A．8cmB．10cmC．12cmD．14cm
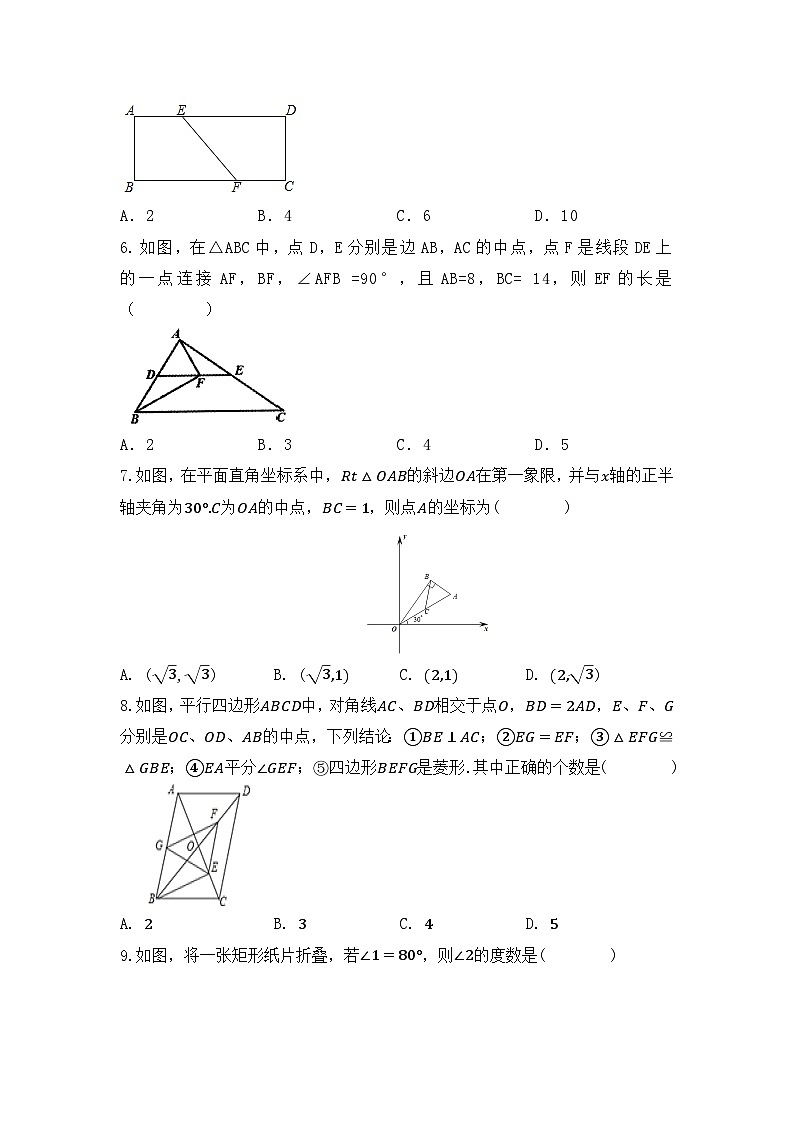
5. 如图，在矩形ABCD中，E，F分别是AD，BC边上的点，，，，，则DE的长为（ ）
A．2B．4C．6D．10
6. 如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点连接AF，BF，∠AFB =90°，且AB=8，BC= 14，则EF的长是 （ ）
A．2B．3C．4D．5
7.如图，在平面直角坐标系中，Rt△OAB的斜边OA在第一象限，并与x轴的正半轴夹角为30°.C为OA的中点，BC=1，则点A的坐标为( )
A. (3,3)B. (3,1)C. (2,1)D. (2,3)
8.如图，平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD、AB的中点，下列结论：①BE⊥AC；②EG=EF；③△EFG≌△GBE；④EA平分∠GEF；⑤四边形BEFG是菱形．其中正确的个数是( )
A. 2B. 3C. 4D. 5
9.如图，将一张矩形纸片折叠，若∠1=80°，则∠2的度数是( )
A. 50°B. 60°C. 70°D. 80°
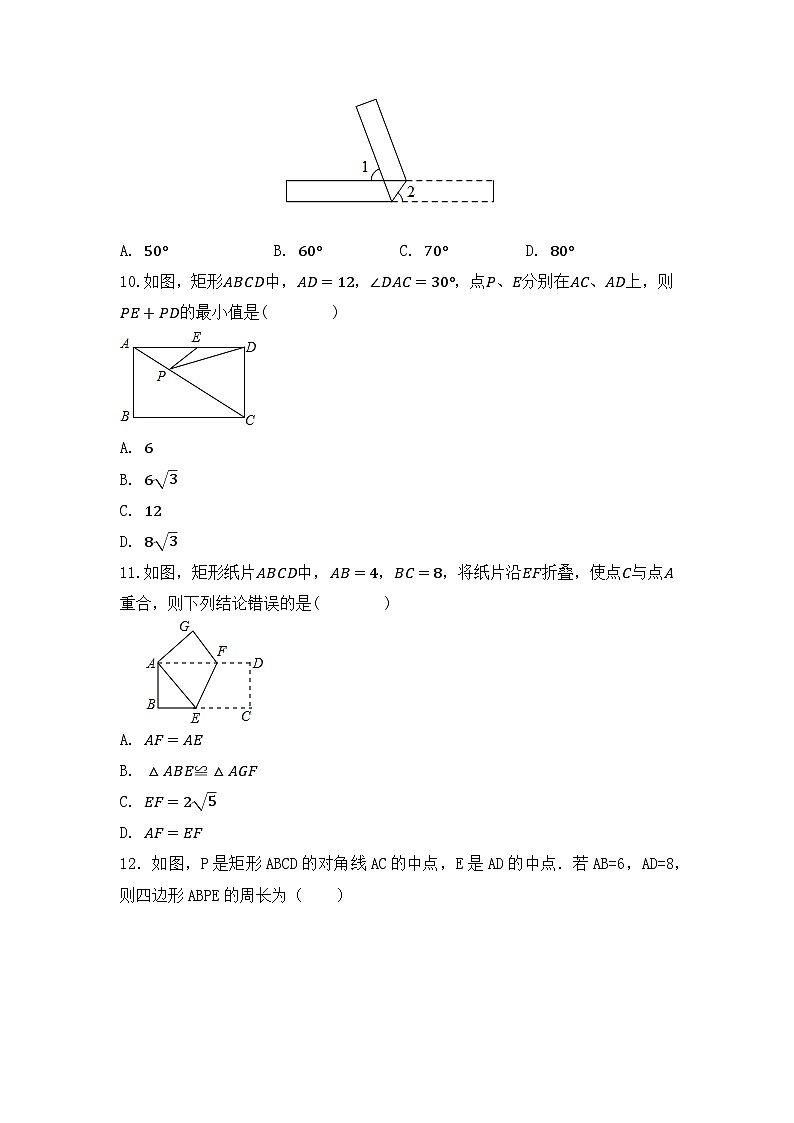
10.如图，矩形ABCD中，AD=12，∠DAC=30°，点P、E分别在AC、AD上，则PE+PD的最小值是( )
A. 6
B. 63
C. 12
D. 83
11.如图，矩形纸片ABCD中，AB=4，BC=8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是( )
A. AF=AE
B. △ABE≌△AGF
C. EF=25
D. AF=EF
12．如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB=6，AD=8，则四边形ABPE的周长为（ ）
A．14B．16C．17D．18
13.如图，在平行四边形ABCD中，M、N是BD上两点，BM＝DN，连接AM、MC、CN、NA，添加一个条件，使四边形AMCN是矩形，这个条件是( )
A.OM＝eq \f(1,2)AC B.MB＝MO C.BD⊥AC D.∠AMB＝∠CND
14.如图所示，公路 AC，BC 互相垂直，公路 AB 的中点 M 与点 C 被湖隔开，若测得 AM 的长为 1.2 km，则 MC 两点间的距离为

A. 0.5 km B. 0.6 km C. 0.9 km D. 1.2 km
二、填空题。
1．如图，在矩形ABCD中，AB=4，BC=6，若点P在AD边上，连接BP、PC，△BPC是以PB为腰的等腰三角形，则PB的长为 ．
2. 如图，是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若最大正方形 M 的边长是 3，则正方形 A，B，C，D，E，F 的面积之和是 ．
3. 如图，矩形 ABCD 中，AB=3，BC=4，P 是边 AD 上的动点，PE⊥AC于点E，PF⊥BD 于点 F，则 PE+PF 的值为： ．
4. 如图，在矩形 ABCD 中，AB=3，AD=4，以 BC 为斜边在矩形的外部作 Rt△BEC，点 F 是 CD 的中点，则 EF 的最大值是 ．
5.如图,在矩形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于12AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则矩形的对角线AC的长为 .
6.如图所示,线段BC为等腰△ABC的底边,矩形ADBE的对角线AB与DE交于点O,若OD=2,则AC= .
三、解答题。
1．如图，在矩形ABCD中．点O在边AB上，∠AOC=∠BOD．求证：AO=OB．
2.已知：如图，在菱形ABCD中，BE⊥AD于点E，延长AD至点F，使DF=AE，连接CF．
(1)判断四边形EBCF的形状，并证明;
(2)若AF=9，CF=3，求CD的长．
3.在Rt△ABC中，∠C＝90°，∠A＝30°，D，E，F分别是AC，AB，BC的中点，连接ED，EF.
(1)求证：四边形DEFC是矩形；
(2)请用无刻度的直尺在图中作出∠ABC的平分线(保留作图痕迹，不写作法).
4. 矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．求证：
(1)四边形AFCE是平行四边形；
(2)EG＝FH.
5.如图,矩形ABCD的对角线AC、BD相交于点O.过点A作AE∥BD,交CB的延长线于点E.
(1)求证:AC=AE;
(2)若∠AOB=120°,AE=8,求BC的长.
6.如图，△ABC 中，AB=BC，过 A 点作 BC 的平行线与 ∠ABC 的平分线交于点 D，连接 OE，CD．
(1)求证四边形 ABCD 是菱形．
(2)连接 AC 与 BD 交于点 O，过点 D 作 DE⊥BC 与 BC 的延长线交于 E 点，连接 EO，若 CE=3，DE=4，求 OE 的长．