湖南省长沙市明德教育集团2023-2024学年八年级下学期期中数学试题(含解析)

这是一份湖南省长沙市明德教育集团2023-2024学年八年级下学期期中数学试题(含解析)，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级 数学试卷 23-24学年第二学期
时量：120分钟 满分：120分
一、选择题（下列选项中，只有一项是符合题意的,请在答题卡中填涂符合题意的选项，本题共10个小题，每小题3分，共30分）
1．下列运算，结果正确的是（ ）
A．B．C．D．
2．下列长度的三条线段，不能组成直角三角形的是（ ）
A．B．
C．D．，，
3．如图，在四边形中，已知，添加下列条件不能判定四边形是平行四边形的是（ ）

A．B．C．D．
4．一次函数的图象不经过第（ ）象限
A．一B．二C．三D．四
5．在平行四边形ABCD中，若，则的度数为（ ）
A．B．C．D．
6．若一次函数的函数值y随自变量x的增大而减小，则m的值可能是（ ）
A．B．C．2D．3
7．如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去高六尺，折高者几何？意思是：一根竹子，原高一丈（一丈＝十尺），一阵风将竹子折断，竹梢恰好抵地，抵地处离竹子底部6尺远，求折断处离地面的高度．设竹子折断处离地面x尺，根据题意，可列方程为（ ）

A．B．
C．D．
8．如图，矩形的对角线，相交于点，，，则边的长为（ ）
A．B．C．D．
9．如图所示，在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连接BE、AF相交于点G，则下列结论不正确的是（ ）
A．BE=AFB．∠DAF=∠BEC
C．AG⊥BED．∠AFB+∠BEC=90°
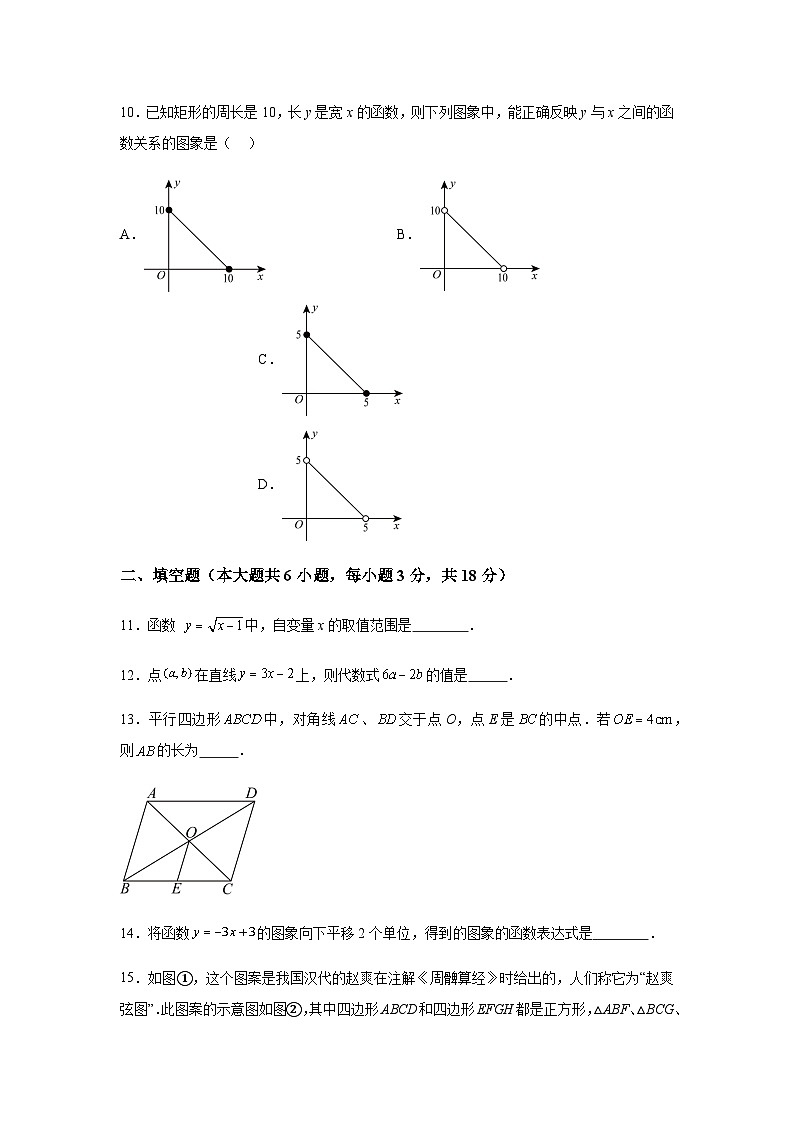
10．已知矩形的周长是10，长y是宽x的函数，则下列图象中，能正确反映y与x之间的函数关系的图象是（ ）
A．B．C．D．
二、填空题（本大题共6小题，每小题3分，共18分）
11．函数 中，自变量x的取值范围是 ．
12．点在直线上，则代数式的值是 ．
13．平行四边形中，对角线、交于点O，点E是的中点．若，则的长为 ．
14．将函数的图象向下平移2个单位，得到的图象的函数表达式是 ．
15．如图①，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图②，其中四边形ABCD和四边形EFGH都是正方形，△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形．若EF=2，DE=8，则AB的长为 ．
16．一次函数的图象经过和，则关于x的不等式的解集为 ．
三、解答题（本题共8个小题，第17、18、19题每题6分，第20、21题每题8分，第22、23每题9分，第24、25每题10分，共72分）
17．计算：．
18．先化简，后求值：，其中
19．如图，已知平行四边形中，是它的一条对角线，过A、C两点作，，垂足分别为E、F，延长、分别交、于点G、H．
(1)求证：四边形是平行四边形；
(2)若，求的长．
20．台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向由行驶向，已知点为海港，并且点与直线上的两点，的距离分别为，，又，以台风中心为圆心周围250km以内为受影响区域．
（1）求的度数；
（2）海港受台风影响吗？为什么？
21．如图，在平面直角坐标系中，直线:与直线l2:相交于，且直线过点．
(1)求直线的函数解析式；
(2)直线与x轴、y轴分别相交于点A、B，直线与x轴、y轴分别相交于点C、D，求的面积．
22．如图，在矩形中，是上一点，连接，，平分．
(1)求证：；
(2)作于点，若，求的长．
23．我校为落实国家“双减”政策，丰富课后服务内容，为学生开设了无人机操作校本课程．现需购买A、B两种型号的无人机．已知2台A型无人机和3台B型无人机共需3400元，4台A型无人机和5台B 型无人机共需6200元．
(1)求A型、B型两种无人机的单价分别是多少元？
(2)学校准备购买A型和B型无人机共100台，购买B型无人机不超过A型无人机的2倍．商家给出购买A型无人机打九折优惠，购买B型无人机打八折优惠，问购买A型无人机多少台时花费最少？最少花费是多少元？
24．我们约定：若关于的一次函数和同时满足，，则称函数和互为“真诚函数”．根据该约定，解答下列问题：
(1)若关于的一次函数和互为“真诚函数”，求，的值；
(2)若关于的一次函数的“真诚函数”经过点，且与的交点P在第三象限，求的取值范围；
(3)在平面直角坐标系中，点，点，若关于的一次函数与它的“真诚函数”交于点N，在平面内是否存在点M，使得以A、B、M、N为顶点的四边形为菱形．若存在，求出M点坐标；若不存在，请说明理由．
25．如图1，在中，，以为边在其右侧作正方形，
图1 图2 图3
(1)求的长；
(2)如图2，若E是线段上一动点，为等腰直角三角形，且为直角，当点E沿方向由P运动到C点时，求F点经过的路径长；
(3)如图3，若E是线段上一动点，连接，与交于点G，判断是否为定值，如果是，请求出该定值；如果不是，请说明理由．
参考答案与解析
1．D
【分析】根据二次根式的运算性质进行计算即可．
【详解】A．与不是同类二次根式，不能合并，此选项错误；
B．3与不是同类二次根式，不能合并，此选项错误；
C．，此选项错误；
D．，此选项计算正确；
故选：D．
【点睛】本题考查了二次根式加减乘除计算，熟知以上计算是解题的关键．
2．A
【分析】本题考查了勾股定理逆定理，熟练掌握勾股定理逆定理知识是解决本题的关键．根据勾股定理的逆定理依次判断即可．
【详解】解：A、 ,因此不能组成直角三角形，故此选项符合题意；
B、 ，因此能组成直角三角形，故此选项不符合题意；
C、 ，因此能组成直角三角形，故此选项不符合题意；
D、 ，因此，，能组成直角三角形，故此选项不符合题意．
故选：A．
3．C
【分析】根据一组对边平行且相等的四边形是平行四边形可知A项不符合题意；根据两组对边分别平行的四边形是平行四边形可知B项不符合题意；根据全等三角形的判定与性质可知D项不符合题意进而即可判断．
【详解】解：∵，，
∴由一组对边平行且相等的四边形是平行四边形，
∴项能判定四边形是平行四边形，
故项不符合题意；
∵，，
∴由两组对边分别平行的四边形是平行四边形，
∴项能判定四边形是平行四边形，
故项不符合题意；
∵，但和不一定平行，
∴项不能判定四边形是平行四边形，
故符合题意；
∵，
∴，
∵，，
∴，
∴，
∴项能判定四边形是平行四边形，
故项不符合题意；
故选：．
【点睛】本题考查了平行四边形的判定，全等三角形的判定与性质，掌握平行四边形的判定是解题的关键．
4．B
【分析】本题主要考查了一次函数图象与系数的关系，熟知对于一次函数，当时，一次函数经过第一、二、三象限，当时，一次函数经过第一、三、四象限， 当时，一次函数经过第一、二、四象限，当时，一次函数经过第二、三、四象限，据此可得答案．
【详解】解：∵一次函数解析式为，，
∴一次函数的图象经过第一、三、四象限，不经过第二象限，
故选：B．
5．C
【分析】本题考查了平行四边形的性质，平行线的性质，掌握平行四边形的性质是解题的关键．
根据平行四边形的性质可得，根据平行线的性质可得，结合已知条件可得，即可求解．
【详解】解：如图，在平行四边形ABCD中，若
四边形是平行四边形，
，
，
，
，
，
故选C．
6．A
【分析】此题考查了一次函数的性质，熟练掌握一次函数的增减性是解题的关键．
根据一次函数随自变量x的增大而减小，列出关于m的不等式，解不等式即可得到答案．
【详解】一次函数的函数值y随自变量x的增大而减小，
，
，
m的值可能是，
故选：A．
7．D
【分析】根据题目设出的未知数，将直角三角形的斜边的长度表示为，再利用勾股定理建立方程．
【详解】解：∵竹子原高十尺，竹子折断处离地面x尺
∴图中直角三角形的斜边长尺
根据勾股定理建立方程得：
故选：D．
【点睛】本题考查了利用勾股定理建立方程解决实际问题，熟记勾股定理，理清题目中的条件和数量关系是解决本题的关键．
8．C
【分析】本题考查矩形的性质，等边三角形的判定与性质，关键是根据矩形的性质得出解答．根据矩形的性质得出，进而利用等边三角形的判定和性质解答即可．
【详解】解：四边形是矩形，
∴，
∵，
∴是等边三角形，
∴，
∵，
∴，
∴．
故选：C．
9．D
【分析】分析图形，根据正方形及三角形性质找到各角边的关系即可求解．
【详解】解：∵ABCD是正方形
∴∠ABF＝∠C＝90°，AB＝BC
∵BF＝CE
∴△ABF≌△BCE
∴AF＝BE（A正确）
∵∠BFA＝∠BEC，
∴ ，
∵ ，
∴（D错误）
∵∠BAF＋∠DAF＝90°，∠BAF＋∠BFA＝90°
∴∠DAF＝∠BEC（B正确）
∵∠BAF＝∠CBE，∠BAF＋∠AFB＝90°
∴∠CBE＋∠AFB＝90°
∴AG⊥BE（C正确）
故选D．
【点睛】此题主要考查了学生对正方形的性质及全等三角形的判定的掌握情况．熟练掌握正方形的性质及全等三角形的判定是解题关键．
10．D
【分析】本题考查了一次函数的图象，正确求出的取值范围是解题关键．
根据矩形的性质可得，再根据特殊点的情况确定的取值范围，由此即可得．
【详解】解：由题意得：，即，
当时，，不符合题意；
当时，，不符合题意；
∴，
∴与之间的函数关系的图象是在内的一条线段（不含两端点），
观察四个选项可知，只有选项D符合，
故选：D．
11．
【分析】本题考查了二次根式有意义的条件，可得，解不等式即可，熟知根号下需要大于等于0，是解题的关键．
【详解】解：根据二次根式的意义，有，
解得，
故自变量x的取值范围是，
故答案为：．
12．4
【分析】本题考查的是一次函数的性质，求解代数式的值，由函数的性质得到是解本题的关键．
把代入函数解析式可得，再代入代数式求值即可．
【详解】点在直线上，
，
，
故答案为：4．
13．##8厘米
【分析】本题主要考查了平行四边形的性质，三角形中位线性质定理，熟知三角形的中位线平行于第三边且其长度等于第三边的一半是解题的关键．
证明是的中位线，即可得到．
【详解】平行四边形中，对角线、交于点O，
点O是的中点，
点E是的中点，
是的中位线，
，
，
故答案为：．
14．##y=1-3x
【分析】直接根据“上加下减”的原则进行解答即可．
【详解】解：由“上加下减”的原则可知，把一次函数的图象向下平移2个单位后所得直线的解析式为：
，即．
故答案为：．
【点睛】本题考查了一次函数图象与几何变换：一次函数y=kx+b（k、b为常数，k≠0）的图象为直线，当直线平移时k不变，当向下平移|m|个单位，则平移后直线的解析式为y=kx+b-|m|，理解“上加下减”是解题的关键．
15．10．
【详解】解：依题意知，BG=AF=DE=8，EF=FG=2，∴BF=BG﹣BF=6，∴直角△ABF中，利用勾股定理得：AB===10．故答案为10．
点睛：此题考查勾股定理的证明，解题的关键是得到直角△ABF的两直角边的长度．
16．
【分析】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数的值大于或小于的自变量x的取值范围；从函数图象的角度看，就是确定直线在x轴上或下方部分所有的点的横坐标所构成的集合．
根据图象得到函数的增减性及与x轴的交点的横坐标，即能求得不等式的解集．
【详解】解：如图所示，
由图象可得：当时，一次函数的图象在x轴上方
∴关于x的不等式的解集为．
故答案为：．
17．
【分析】本题考查了实数的混合运算，熟练掌握运算法则和正确化简每一项是解题的关键．
依次化简计算零指数幂，绝对值，算术平方根，负整数指数幂即可．
【详解】解：原式
．
18．
【分析】本题考查了完全平方公式的运算，实数的化简求值，熟练掌握公式及运算法则是解决此类题的关键．
根据完全平方公式、整式的加减运算法则进行运算即可，最后代入数据即可求解．
【详解】解：
，
当时，
原式．
19．(1)见解析
(2)5
【分析】本题考查平行四边形的判定和性质，解题的关键是熟练掌握平行四边形的判定和性质．
（1）根据平行线的判定和性质证明即可；
（2）由（1）中结果得出，再由平行线的性质求解即可
【详解】（1）证明：，，
，
四边形是平行四边形，
，
四边形是平行四边形；
（2）由（1）得四边形是平行四边形，
∴，
∵，
∴，
∵平行四边形，
∴．
20．（1）90°；（2）受台风影响，理由见解析
【分析】（1）利用勾股定理的逆定理得出△ABC是直角三角形，进而得出∠ACB的度数；
（2）利用三角形面积得出CD的长，进而得出海港C是否受台风影响．
【详解】解：（1）∵AC=300km，BC=400km，AB=500km，
∴AC2+BC2=AB2，
∴△ABC是直角三角形，∠ACB=90°；
（2）海港C受台风影响，
理由：过点C作CD⊥AB，
∵△ABC是直角三角形，
∴AC×BC=CD×AB，
∴300×400=500×CD，
∴CD=240（km），
∵以台风中心为圆心周围250km以内为受影响区域，
∴海港C受台风影响．
【点睛】本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．
21．(1)
(2)14
【分析】题目主要考查一次函数的基本性质，确定一次函数解析式及交点求面积，熟练掌握一次函数的性质是解题关键
（1）根据待定系数法确定函数解析式即可；
（2）先确定点B、D坐标，然后结合图形求面积即可
【详解】（1）解：∵直线l2:相交于，且直线过点，
∴代入得：，
解得：，
∴直线的函数解析式为：；
（2）直线:，当时，，
∴；
直线l2: ，当时，，
∴；
∴，
∵，
∴的面积为：．
22．(1)详见详解
(2)5
【分析】此题重点考查矩形的性质、平行线的性质、等腰三角形的判定、全等三角形的判定与性质、勾股定理等知识，证明及是解题的关键．
（1）由矩形的性质得，则，而，所以，则；
（2）由于点，得，可证明，得，所以，而，勾股定理得即可求解．
【详解】（1）证明：四边形是矩形，
，
，
平分，
，
，
．
（2）解：于点，
，
在和中，
，
，
，
，
，
，
∵，
∴．
23．(1)A型无人机的单价是800元、B型无人机的单价是600元
(2)买A型无人机34台时花费最少，最少花费56160元．
【分析】本题考查了二元一次方程组的应用，一次函数的应用，一元一次不等式的应用，解答本题的关键是明确题意，利用一次函数得性质和方程的知识解答；
（1）根据2台A型无人机和3台B型无人机共需3400元，4台A型无人机和5台B 型无人机共需6200元，可列出相应的二元一次方程组，即可求解；
（2）设购买A型无入机m台，花费W元，根据题意，先求出m的取值范围，再列出W关于m的函数关系式，然后根据一次函数的性质，即可求解．
【详解】（1）解：设A型无人机的单价是x元、B型无人机的单价是y元，
根据题意得：，
解得：，
答：设A型无人机的单价是800元、B型无人机的单价是600元；
（2）设购买购买A型无人机m台，则购买B型无人机台，花费了W元
购买B型无人机不超过A型无人机的2倍，
，
解得：，
商家给出购买A型无人机打九折优惠，购买B型无人机打八折优惠，
，
，
随m的增大而增大，
当m取最小整数34时，W有最小值，
元，
答：买A型无人机34台时花费最少，最少花费是56160元．
24．(1)
(2)
(3)或或或或
【分析】题目主要考查一次函数的性质及新定义，算术平方根及平方的非负性，直线交点问题等，理解新定义是解题关键．
（1）根据题意得出，即可得出结果；
（2）根据新定义确定关于的一次函数的“真诚函数”为，且经过点，代入得出，然后联立两个一次函数得出交点，确定不等式求解即可；
（3）由（2）得关于的一次函数与它的“真诚函数”交于点，分三种情况分析：当以为对角线时，构成菱形，当以为对角线时，构成菱形，当以为对角线时，构成菱形，分别利用菱形的性质求解即可．
【详解】（1）解：∵关于的一次函数和互为“真诚函数”，
∴，
∴；
（2）∵关于的一次函数和同时满足，，则称函数和互为“真诚函数”．
∴，
∴关于的一次函数的“真诚函数”为，且经过点，代入得：
，得，
联立两个函数：，解得：，
∵交点P在第三象限，
∴，
∴，
解得：；
（3）由（2）得关于的一次函数与它的“真诚函数”交于点，
设，
点，点，
当以为对角线时，构成菱形，
∴，即，
解的：或，
∴或；
当以为对角线时，构成菱形，
∴，即，
解的：或6，
∴或；
当以为对角线时，构成菱形，
∴，即，
解的：或6，
∴；
综上可得：或或或或．
25．(1)3
(2)
(3)为定值，
【分析】题目主要考查含30度角的直角三角形的性质，勾股定理解三角形，正方形的性质，动点问题及等腰三角形的判定和性质，作出辅助线，综合运用这些知识点是解题关键．
（1）根据题意，利用含30度角的直角三角形的性质及勾股定理求解即可；
（2）当点E与点P重合时，点F位置如图，过点F作，利用全等三角形的判定和性质得出当点E移动到点B时，点F与点C重合，此时运动路径为线段，再由勾股定理求解；当点E从点B开始到点C时，运动路径为线段，继续利用勾股定理求解即可得出结果；
（3）连接，根据正方形的性质及全等三角形的判定和性质得出，，设，分别利用三角形内角和定理及外角的性质得出各角之间的关系，再由等角对等边及等腰直角三角形的性质确定点G为中点，即可求解．
【详解】（1）解：∵在中，，
∴，
∵，
∴，
∴，
∵以为边在其右侧作正方形，
∴；
（2）如图所示，当点E与点P重合时，点F位置如图，过点F作，如图所示：
∴，
∴，
根据题意得为等腰直角三角形，
∴，
∵，
∴，
∴，，
∴，
当点E移动到点B时，点F与点C重合，此时运动路径为线段，
∴，
当点E从点B开始到点C时，运动路径为线段，
此时，
∴F点经过的路径长为；
（3）连接，如图所示：
∵正方形，
∴，
∵，
∴，
∴，，
设，
则，，
∴，
∴，
∵，，
∴，
∴，
∴，
∴，
∴点G为中点，
∵，
∴，
∴．