平面向量、复数 专题训练-2025届高三数学二轮专题复习

这是一份平面向量、复数 专题训练-2025届高三数学二轮专题复习，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.[2024·浙江名校联考]已知i为虚数单位，则eq \f(1＋2i,2＋i)在复平面上对应的点在( )
A.第一象限 B.第二象限C.第三象限 D.第四象限
2.[2024·嘉兴模拟]在平行四边形ABCD中，点E，F分别在边BC，CD上，且eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，eq \(CF,\s\up6(→))＝3eq \(FD,\s\up6(→))，记eq \(AB,\s\up6(→))＝a，eq \(AD,\s\up6(→))＝b，则eq \(EF,\s\up6(→))＝( )
A.－eq \f(3,4)a＋eq \f(1,3)b B.eq \f(3,4)a＋eq \f(1,3)bC.eq \f(3,4)a－eq \f(1,3)b D.－eq \f(1,4)a＋eq \f(1,3)b
3.[2024·广东六校联考]设复数z＝eq \f(1,2)＋eq \f(\r(3),2)i，其中i是虚数单位，eq \(z,\s\up6(－))是z的共轭复数，下列结论中错误的是( )
A.zeq \(z,\s\up6(－))＝1
B.z2＝eq \(z,\s\up6(－))
C.z是方程x2－x＋1＝0的一个根
D.满足zn∈R的最小正整数n为3
4.[2024·安徽名校联考]已知向量a＝(1，2)，b＝(2，x)，若a⊥b，则|2a＋b|＝( )
A.3eq \r(2) B.4 C.5 D.4eq \r(2)
5.[2024·惠州质检]已知向量a＝(2eq \r(3)，2)，向量e＝(eq \f(1,2)，eq \f(\r(3),2))，则向量a在向量e上的投影向量为( )
A.(eq \r(3)，3) B.(－eq \r(3)，1) C.(1，eq \r(3)) D.(eq \f(1,4)，eq \f(\r(3),4))
6.[2024·广州调研]已知复数z满足|z－1|＝|z＋i|(i为虚数单位)，在复平面内，记z0＝2＋i对应的点为点Z0，z对应的点为点Z，则点Z0与点Z之间距离的最小值为( )
A.eq \f(\r(2),2) B.eq \r(2) C.eq \f(3\r(2),2) D.2eq \r(2)
7.[2024·南京质检]△ABC中，AH为BC边上的高且eq \(BH,\s\up6(→))＝3eq \(HC,\s\up6(→))，动点P满足eq \(AP,\s\up6(→))·eq \(BC,\s\up6(→))＝－eq \f(1,4)eq \(BC,\s\up6(→))2，则点P的轨迹一定过△ABC的( )
A.外心 B.内心 C.垂心 D.重心
8.[2024·泉州模拟]人脸识别，是基于人的脸部特征信息进行身份识别的一种生物识别技术.在人脸识别中，主要应用距离测试检测样本之间的相似度，常用测量距离的方式有曼哈顿距离和余弦距离.设A(x1，y1)，B(x2，y2)，则曼哈顿距离d(A，B)＝|x1－x2|＋|y1－y2|，余弦距离e(A，B)＝1－cs(A，B)，其中cs(A，B)＝cs〈eq \(OA,\s\up6(→))，eq \(OB,\s\up6(→))〉(O为坐标原点).已知M(2，1)，d(M，N)＝1，则e(M，N)的最大值近似等于( )
(参考数据：eq \r(2)≈1.41，eq \r(5)≈2.24)

二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9.[2024·湖南六校联考]已知向量a＝(1，0)，b＝(0，1)，c＝(1，1).在下列各组向量中，可以作为平面内所有向量的一个基底的是( )
A.{a，c} B.{a，b－c}C.{c，a＋b} D.{a＋b，b－c}
10.[2024·滨州质检]欧拉公式eix＝cs x＋isin x(e为自然对数的底数，i为虚数单位)是由瑞士著名数学家欧拉创立，该公式建立了三角函数与指数函数的关系，在复变函数论中占有非常重要的地位，被誉为“数学中的天桥”.依据欧拉公式，则下列结论中正确的是( )
A.复数eieq \f(π,2)为纯虚数
B.复数ei2对应的点位于第二象限
C.复数eieq \f(π,3)的共轭复数为eq \f(\r(3),2)－eq \f(1,2)i
D.复数eiθ(θ∈R)在复平面内对应的点的轨迹是圆
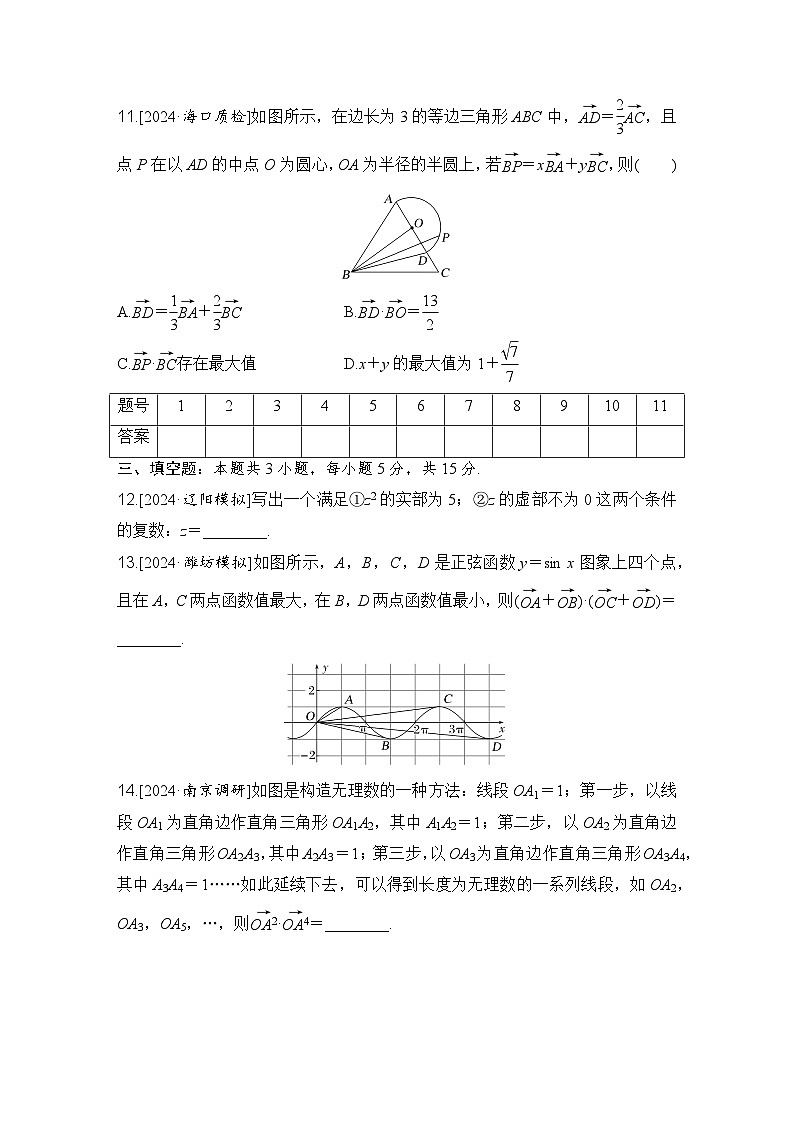
11.[2024·海口质检]如图所示，在边长为3的等边三角形ABC中，eq \(AD,\s\up6(→))＝eq \f(2,3)eq \(AC,\s\up6(→))，且点P在以AD的中点O为圆心，OA为半径的半圆上，若eq \(BP,\s\up6(→))＝xeq \(BA,\s\up6(→))＋yeq \(BC,\s\up6(→))，则( )
A.eq \(BD,\s\up6(→))＝eq \f(1,3)eq \(BA,\s\up6(→))＋eq \f(2,3)eq \(BC,\s\up6(→)) B.eq \(BD,\s\up6(→))·eq \(BO,\s\up6(→))＝eq \f(13,2)
C.eq \(BP,\s\up6(→))·eq \(BC,\s\up6(→))存在最大值 D.x＋y的最大值为1＋eq \f(\r(7),7)
三、填空题：本题共3小题，每小题5分，共15分.
12.[2024·辽阳模拟]写出一个满足①z2的实部为5；②z的虚部不为0这两个条件的复数：z＝________.
13.[2024·潍坊模拟]如图所示，A，B，C，D是正弦函数y＝sin x图象上四个点，且在A，C两点函数值最大，在B，D两点函数值最小，则(eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→)))·(eq \(OC,\s\up6(→))＋eq \(OD,\s\up6(→)))＝________.
14.[2024·南京调研]如图是构造无理数的一种方法：线段OA1＝1；第一步，以线段OA1为直角边作直角三角形OA1A2，其中A1A2＝1；第二步，以OA2为直角边作直角三角形OA2A3，其中A2A3＝1；第三步，以OA3为直角边作直角三角形OA3A4，其中A3A4＝1……如此延续下去，可以得到长度为无理数的一系列线段，如OA2，OA3，OA5，…，则eq \(OA2,\s\up6(→))·eq \(OA4,\s\up6(→))＝________.
四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤.
15.(13分)[2024·济宁模拟]已知复数z1＝t＋(t2－1)i，z2＝sin θ＋(2cs θ＋1)i，其中t∈R，θ∈[0，π].
(1)若z1，z2∈R，且z1＞z2，求t的值；
(2)若z1＝z2，求θ.
16.(15分) [2024·聊城模拟]如图，在平面直角坐标系中，三个向量eq \(OA,\s\up6(→))，eq \(OB,\s\up6(→))，eq \(OC,\s\up6(→))满足条件：|eq \(OA,\s\up6(→))|＝2|eq \(OB,\s\up6(→))|＝2|eq \(OC,\s\up6(→))|＝2，eq \(OA,\s\up6(→))与eq \(OC,\s\up6(→))的夹角为α，且tan α＝2，eq \(OB,\s\up6(→))与eq \(OC,\s\up6(→))的夹角为45°.
(1)求点A，B，C的坐标；
(2)若点P为线段OC上的动点，当eq \(PO,\s\up6(→))·eq \(PA,\s\up6(→))取得最小值时，求点P的坐标.
17.(15分)[2024·佛山模拟]在△ABC中，角A，B，C的对边分别为a，b，c，c·sin A＝a·cs C，设△ABC的面积为S，S＝eq \f(\r(2),4)bc.
(1)求角B的大小；
(2)若a＝3，过△ABC的重心G的直线l与边a，c的交点分别为E，F，eq \(BC,\s\up6(→))＝λeq \(BE,\s\up6(→))，eq \(BA,\s\up6(→))＝μeq \(BF,\s\up6(→))，
请计算λ＋μ的值.
18.(17分) [2023·镇江模拟]数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感.莱洛三角形的画法：先画等边三角形ABC，再分别以点A，B，C为圆心，线段AB长为半径画圆弧，便得到莱洛三角形.如图所示，已知AB＝2，O为BC的中点，点P，Q分别在弧AC、弧AB上，设∠PBC＝∠ACQ＝θ.
(1)当θ＝eq \f(π,6)时，求|eq \(PQ,\s\up6(→))|；
(2)求eq \(OP,\s\up6(→))·eq \(OQ,\s\up6(→))的取值范围.
19.(17分)[2024·广州质检]已知△ABC的内角A，B，C所对的边分别为a，b，c，向量m＝(b，a＋c)，n＝(b－c，c－a)，m⊥n.
(1)若a＝8，eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))＝8，D为边BC的中点，求中线AD的长度；
(2)若E为边BC上一点，且AE＝1，BE∶EC＝2c∶b，求2b＋c的最小值.
平面向量、复数
1.A [eq \f(1＋2i,2＋i)＝eq \f(（1＋2i）（2－i）,（2＋i）（2－i）)＝eq \f(4＋3i,5)，其在复平面上对应的点的坐标为(eq \f(4,5)，eq \f(3,5))，位于第一象限.故选A.]
2.A [因为eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，eq \(CF,\s\up6(→))＝3eq \(FD,\s\up6(→))，
所以eq \(EF,\s\up6(→))＝eq \(CF,\s\up6(→))－eq \(CE,\s\up6(→))＝eq \f(3,4)eq \(CD,\s\up6(→))－eq \f(1,3)eq \(CB,\s\up6(→))＝
－eq \f(3,4)eq \(AB,\s\up6(→))＋eq \f(1,3)eq \(AD,\s\up6(→))＝－eq \f(3,4)a＋eq \f(1,3)b.故选A.]
3.B [对于A，z·eq \(z,\s\up6(－))＝(eq \f(1,2)＋eq \f(\r(3),2)i)(eq \f(1,2)－eq \f(\r(3),2)i)＝1，故A正确；
对于B，z2＝(eq \f(1,2)＋eq \f(\r(3),2)i)2＝－eq \f(1,2)＋eq \f(\r(3),2)i，
eq \(z,\s\up6(－))＝eq \f(1,2)－eq \f(\r(3),2)i，z2＝－eq \(z,\s\up6(－))，故B错误；
对于C，(eq \f(1,2)＋eq \f(\r(3),2)i)2－(eq \f(1,2)＋eq \f(\r(3),2)i)＋1＝
－eq \f(1,2)＋eq \f(\r(3),2)i－eq \f(1,2)－eq \f(\r(3),2)i＋1＝0，则z是方程x2－x＋1＝0的一个根，故C正确；
对于D，z＝eq \f(1,2)＋eq \f(\r(3),2)i，z2＝－eq \f(1,2)＋eq \f(\r(3),2)i，z3＝z2·z＝－(eq \f(1,2)－eq \f(\r(3),2)i)(eq \f(1,2)＋eq \f(\r(3),2)i)＝－1，故D正确.故选B.]
4.C [因为a⊥b，所以a·b＝1×2＋2x＝0，
所以x＝－1，则2a＋b＝2(1，2)＋(2，－1)＝(4，3)，所以|2a＋b|＝eq \r(42＋32)＝5.故选C.]
5.A [向量a在向量e上的投影向量为eq \f(a·e,|e|2)e＝2eq \r(3)×(eq \f(1,2)，eq \f(\r(3),2))＝(eq \r(3)，3).故选A.]
6.C [设z＝x＋yi(x，y∈R)，
由|z－1|＝|z＋i|，
得(x－1)2＋y2＝x2＋(y＋1)2，即y＝－x，
所以点Z0(2，1)与点Z(x，y)之间的距离
d＝eq \r(（x－2）2＋（y－1）2)＝eq \r(2x2－2x＋5)
＝eq \r(2（x－\f(1,2)）2＋\f(9,2))≥eq \f(3\r(2),2)，
当且仅当x＝eq \f(1,2)时取等号.选C.]
7.A [如图，以点H为坐标原点建立平面直角坐标系，
设|BC|＝4a，|AH|＝b，则H(0，0)，A(0，b)，B(－3a，0)，C(a，0)，所以eq \(BC,\s\up6(→))＝(4a，0).
设P(x，y)，则eq \(AP,\s\up6(→))＝(x，y－b)，
所以eq \(AP,\s\up6(→))·eq \(BC,\s\up6(→))＝4ax，
则由eq \(AP,\s\up6(→))·eq \(BC,\s\up6(→))＝－eq \f(1,4)eq \(BC,\s\up6(→))2，
得4ax＝－4a2，所以x＝－a，所以点P在线段BC的垂直平分线上，所以点P的轨迹一定过△ABC的外心，故选A.]
8.B [设N(x，y)，由题意可得：
d(M，N)＝|2－x|＋|1－y|＝1，
即|x－2|＋|y－1|＝1，
可知|x－2|＋|y－1|＝1表示正方形ABCD，其中A(2，0)，B(3，1)，C(2，2)，D(1，1)，如图所示，
即点N在正方形ABCD的边上运动.
因为eq \(OM,\s\up6(→))＝(2，1)，eq \(ON,\s\up6(→))＝(x，y)，
由图可知：当cs(M，N)＝cs〈eq \(OM,\s\up6(→))，eq \(ON,\s\up6(→))〉取到最小值，即〈eq \(OM,\s\up6(→))，eq \(ON,\s\up6(→))〉最大，点N有如下两种可能：
①点N为点A，
则eq \(ON,\s\up6(→))＝(2，0)，
可得cs(M，N)＝cs〈eq \(OM,\s\up6(→))，eq \(ON,\s\up6(→))〉
＝eq \f(4,\r(5)×2)＝eq \f(2\r(5),5)；
②点N在线段CD上运动时，此时eq \(ON,\s\up6(→))与eq \(DC,\s\up6(→))同向，不妨取eq \(ON,\s\up6(→))＝(1，1)，
则cs(M，N)＝cs〈eq \(OM,\s\up6(→))，eq \(ON,\s\up6(→))〉
＝eq \f(3,\r(5)×\r(2))＝eq \f(3\r(10),10).
因为eq \f(3\r(10),10)＞eq \f(2\r(5),5)，
所以e(M，N)的最大值为1－eq \f(2\r(5),5)≈0.104.
故选B.]
9.AD [对于A，因为a＝(1，0)，c＝(1，1)，所以1×1≠0×1，所以a与c不共线，所以{a，c}可以作为平面内所有向量的一个基底，所以选项A正确；
对于B，b＝(0，1)，c＝(1，1)，则b－c＝(－1，0)，又a＝(1，0)，所以b－c＝－a，
即(b－c)∥a，所以{a，b－c}不可以作为平面内所有向量的一个基底，所以选项B错误；
对于C，a＋b＝(1，1)＝c，所以(a＋b)∥c，所以{c，a＋b}不可以作为平面内所有向量的一个基底，所以选项C错误；
对于D，a＋b＝(1，1)，b－c＝(－1，0)，所以1×0≠1×(－1)，所以a＋b与b－c不共线，所以{a＋b，b－c}可以作为平面内所有向量的一个基底，所以选项D正确.综上，选AD.]
10.ABD [对A：因为复数eieq \f(π,2)＝cseq \f(π,2)＋
isin eq \f(π,2)＝i为纯虚数，故选项A正确；
对B：复数ei2＝cs 2＋isin 2，
因为cs 2＜0，sin 2＞0，所以复数ei2对应的点为(cs 2，sin 2)位于第二象限，B正确；
对C：复数eieq \f(π,3)＝cs eq \f(π,3)＋isin eq \f(π,3)＝eq \f(1,2)＋eq \f(\r(3),2)i的共轭复数为eq \f(1,2)－eq \f(\r(3),2)i，故选项C错误；
对D：复数eiθ＝cs θ＋isin θ(θ∈R)在复平面内对应的点为(cs θ，sin θ)，因为cs2θ＋sin2θ＝1，所以复数eiθ(θ∈R)在复平面内对应的点的轨迹是圆，故选项D正确.故选ABD.]
11.ABC [对于A，因为eq \(AD,\s\up6(→))＝eq \f(2,3)eq \(AC,\s\up6(→))，且点P在以AD的中点O为圆心，OA为半径的半圆上，所以OA＝OD＝DC＝eq \f(1,3)AC，则eq \(BD,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \(CD,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \f(1,3)eq \(CA,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \f(1,3)(eq \(BA,\s\up6(→))－eq \(BC,\s\up6(→)))＝eq \f(1,3)eq \(BA,\s\up6(→))＋eq \f(2,3)eq \(BC,\s\up6(→))，故A正确；
eq \(BO,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \(CO,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \f(2,3)eq \(CA,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \f(2,3)(eq \(BA,\s\up6(→))－eq \(BC,\s\up6(→)))＝eq \f(2,3)eq \(BA,\s\up6(→))＋eq \f(1,3)eq \(BC,\s\up6(→))，
则eq \(BD,\s\up6(→))·eq \(BO,\s\up6(→))＝(eq \f(1,3)eq \(BA,\s\up6(→))＋eq \f(2,3)eq \(BC,\s\up6(→)))·(eq \f(2,3)eq \(BA,\s\up6(→))＋eq \f(1,3)eq \(BC,\s\up6(→)))
＝eq \f(2,9)eq \(BA,\s\up6(→))2＋eq \f(2,9)eq \(BC,\s\up6(→))2＋eq \f(5,9)eq \(BA,\s\up6(→))·eq \(BC,\s\up6(→))＝2＋2＋eq \f(5,9)×3×3×eq \f(1,2)＝eq \f(13,2)，故B正确；
如图，以点O为原点，CA所在直线为x轴，建立平面直角坐标系，则A(1，0)，B(－eq \f(1,2)，eq \f(3\r(3),2))，C(－2，0).因为点P在以AD的中点O为圆心，OA为半径的单位圆上，且在x轴的下半部分，
所以设P(cs α，sin α)，α∈[π，2π]，
则eq \(BP,\s\up6(→))＝(cs α＋eq \f(1,2)，sin α－eq \f(3\r(3),2))，
又eq \(BC,\s\up6(→))＝(－eq \f(3,2)，－eq \f(3\r(3),2))，
所以eq \(BP,\s\up6(→))·eq \(BC,\s\up6(→))＝－eq \f(3,2)cs α－eq \f(3,4)－eq \f(3\r(3),2)sin α＋eq \f(27,4)＝－3cs(α－eq \f(π,3))＋6.
因为α∈[π，2π]，所以α－eq \f(π,3)∈[eq \f(2π,3)，eq \f(5π,3)]，
所以当α－eq \f(π,3)＝π，即α＝eq \f(4π,3)时，eq \(BP,\s\up6(→))·eq \(BC,\s\up6(→))取得最大值9，故C正确；
因为eq \(BP,\s\up6(→))＝xeq \(BA,\s\up6(→))＋yeq \(BC,\s\up6(→))，eq \(BA,\s\up6(→))＝(eq \f(3,2)，－eq \f(3\r(3),2))，所以(cs α＋eq \f(1,2)，sin α－eq \f(3\r(3),2))＝
x(eq \f(3,2)，－eq \f(3\r(3),2))＋y(－eq \f(3,2)，－eq \f(3\r(3),2))，
即(cs α＋eq \f(1,2)，sin α－eq \f(3\r(3),2))
＝(eq \f(3,2)(x－y)，－eq \f(3\r(3),2)(x＋y))，
所以sin α－eq \f(3\r(3),2)＝－eq \f(3\r(3),2)(x＋y)，
所以x＋y＝－eq \f(2\r(3),9)sin α＋1.
因为α∈[π，2π]，所以当α＝eq \f(3π,2)时，x＋y取得最大值eq \f(2\r(3),9)＋1，故D错误.故选ABC.]
12.3＋2i(答案不唯一) [设z＝a＋bi(a，b∈R)，则z2＝a2－b2＋2abi，依题意可得a2－b2＝5，b≠0.故可取a＝3，b＝2，z＝3＋2i.(答案不唯一)]
13.12π2 [由题图知，A(eq \f(π,2)，1)，B(eq \f(3π,2)，－1)，C(eq \f(5π,2)，1)，D(eq \f(7π,2)，－1)，
所以eq \(OA,\s\up6(→))＝(eq \f(π,2)，1)，eq \(OB,\s\up6(→))＝(eq \f(3π,2)，－1)，
eq \(OC,\s\up6(→))＝(eq \f(5π,2)，1)，eq \(OD,\s\up6(→))＝(eq \f(7π,2)，－1)，
所以eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→))＝(2π，0)，eq \(OC,\s\up6(→))＋eq \(OD,\s\up6(→))＝(6π，0)，
所以(eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→)))·(eq \(OC,\s\up6(→))＋eq \(OD,\s\up6(→)))＝2π×6π＋0×0＝12π2.]
14.2－eq \f(\r(6),3) [由题意，得OA2＝eq \r(OAeq \\al(2,1)＋A1Aeq \\al(2,2))＝eq \r(2)，
所以OA3＝eq \r(OAeq \\al(2,2)＋A2Aeq \\al(2,3))＝eq \r(3)，OA4＝eq \r(OAeq \\al(2,3)＋A3Aeq \\al(2,4))＝2，
所以cs ∠A2OA3＝eq \f(OA2,OA3)＝eq \f(\r(2),\r(3))＝eq \f(\r(6),3)，
sin ∠A2OA3＝eq \f(A2A3,OA3)＝eq \f(1,\r(3))＝eq \f(\r(3),3)，
cs ∠A3OA4＝eq \f(OA3,OA4)＝eq \f(\r(3),2)，
sin ∠A3OA4＝eq \f(A3A4,OA4)＝eq \f(1,2)，
所以cs ∠A2OA4＝cs(∠A2OA3＋∠A3OA4)
＝cs ∠A2OA3cs ∠A3OA4－sin ∠A2OA3·
sin ∠A3OA4
＝eq \f(\r(6),3)×eq \f(\r(3),2)－eq \f(\r(3),3)×eq \f(1,2)＝eq \f(\r(2),2)－eq \f(\r(3),6)，
所以eq \(OA2,\s\up6(→))·eq \(OA4,\s\up6(→))＝|eq \(OA2,\s\up6(→))||eq \(OA4,\s\up6(→))|·
cs ∠A2OA4
＝eq \r(2)×2×(eq \f(\r(2),2)－eq \f(\r(3),6))＝2－eq \f(\r(6),3).]
15.解 (1)∵z1∈R，∴t2－1＝0，t＝±1.
∵z2∈R，∴2cs θ＋1＝0，cs θ＝－eq \f(1,2)，
又θ∈[0，π]，∴θ＝eq \f(2π,3).
又z1＞z2，则t＞sin θ＝sin eq \f(2π,3)＝eq \f(\r(3),2)，
故t＝1.
(2)∵z1＝z2，∴t＝sin θ，
且t2－1＝2cs θ＋1，
则sin2θ－1＝2cs θ＋1，则cs2θ＋2cs θ＋1＝0，
即(cs θ＋1)2＝0，得cs θ＝－1，所以θ＝π.
16.解 (1)由tan α＝2知α为锐角，
则sin α＝eq \f(2\r(5),5)，cs α＝eq \f(\r(5),5)，
∴cs(45°＋α)＝－eq \f(\r(10),10)，
sin(45°＋α)＝eq \f(3\r(10),10)，
∴点A，B，C的坐标分别是(2，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(10),10)，\f(3\r(10),10)))，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5),5)，\f(2\r(5),5))).
(2)设eq \(OP,\s\up6(→))＝teq \(OC,\s\up6(→))(0≤t≤1)，
由(1)知，
eq \(OP,\s\up6(→))＝teq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5),5)，\f(2\r(5),5)))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5),5)t，\f(2\r(5),5)t))，
eq \(PO,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(5),5)t，－\f(2\r(5),5)t))，
eq \(PA,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(2－\f(\r(5),5)t，－\f(2\r(5),5)t))，
∴eq \(PA,\s\up6(→))·eq \(PO,\s\up6(→))
＝－eq \f(\r(5),5)teq \b\lc\(\rc\)(\a\vs4\al\c1(2－\f(\r(5),5)t))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(2\r(5),5)t))eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(2\r(5),5)t))
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(t－\f(\r(5),5)))eq \s\up12(2)－eq \f(1,5)，
又∵0≤t≤1，
∴当t＝eq \f(\r(5),5)时，eq \(PO,\s\up6(→))·eq \(PA,\s\up6(→))有最小值为－eq \f(1,5)，
此时点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,5)，\f(2,5))).
17.解 (1)在△ABC中，根据正弦定理
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)，结合条件
c·sin A＝a·cs C，
可得sin C·sin A＝sin A·cs C.
因为A∈(0，π)，
所以sin A≠0，
可得sin C＝cs C，
即有tan C＝1，
又C∈(0，π)，故C＝eq \f(π,4).
又因为S＝eq \f(1,2)ab·sin C＝eq \f(\r(2),4)ab＝eq \f(\r(2),4)bc，
可得a＝c，
即可得A＝C＝eq \f(π,4).
根据A＋B＋C＝π，由此即可得B＝eq \f(π,2).
(2)设AC的中点为D，连接BD(图略)，
利用“重心”的性质可得eq \(BD,\s\up6(→))＝eq \f(3,2)eq \(BG,\s\up6(→))，
又eq \(BD,\s\up6(→))＝eq \f(1,2)eq \(BA,\s\up6(→))＋eq \f(1,2)eq \(BC,\s\up6(→))，
故根据条件eq \(BC,\s\up6(→))＝λeq \(BE,\s\up6(→))，eq \(BA,\s\up6(→))＝μeq \(BF,\s\up6(→))，
可得eq \f(3,2)eq \(BG,\s\up6(→))＝eq \f(λ,2)eq \(BE,\s\up6(→))＋eq \f(μ,2)eq \(BF,\s\up6(→))，
即eq \(BG,\s\up6(→))＝eq \f(λ,3)eq \(BE,\s\up6(→))＋eq \f(μ,3)eq \(BF,\s\up6(→))，
又因为点G，E，F在一条直线上，从而可得eq \f(λ,3)＋eq \f(μ,3)＝1，故λ＋μ＝3.
18.
解 (1)当θ＝eq \f(π,6)时，设BP与CQ的交点为M，连接OQ，OP，PQ，
则CQ⊥AB，
BP⊥AC，
故∠QMP＝∠BMC＝eq \f(2π,3)，
BM＝eq \f(2\r(3),3)，MP＝MQ＝2－eq \f(2\r(3),3)，
故QP＝2×eq \f(\r(3),2)MP＝eq \r(3)eq \b\lc\(\rc\)(\a\vs4\al\c1(2－\f(2\r(3),3)))
＝2eq \r(3)－2，
即|eq \(PQ,\s\up6(→))|＝2eq \r(3)－2.
(2)eq \(OP,\s\up6(→))·eq \(OQ,\s\up6(→))＝(eq \(OB,\s\up6(→))＋eq \(BP,\s\up6(→)))·(eq \(OC,\s\up6(→))＋eq \(CQ,\s\up6(→)))
＝－1＋eq \(OB,\s\up6(→))·eq \(CQ,\s\up6(→))＋eq \(BP,\s\up6(→))·eq \(OC,\s\up6(→))＋eq \(BP,\s\up6(→))·eq \(CQ,\s\up6(→))
＝－1＋2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))＋2cs θ＋2×2×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))＝eq \r(3)sin θ＋3cs θ－3
＝2eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,3)))－3，
由θ∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,3)))，得θ＋eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(2π,3)))，
故sineq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,3)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(3),2)，1))，
则eq \(OP,\s\up6(→))·eq \(OQ,\s\up6(→))∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，2\r(3)－3)).
即eq \(OP,\s\up6(→))·eq \(OQ,\s\up6(→))的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(0，2\r(3)－3)).
19.解 (1)∵向量m＝(b，a＋c)，
n＝(b－c，c－a)，m⊥n，
∴m·n＝b2－bc＋c2－a2＝0，
即b2＋c2－a2＝bc，
∴cs A＝eq \f(b2＋c2－a2,2bc)＝eq \f(1,2)，
又A∈(0，π)，∴A＝eq \f(π,3).
∵D为边BC的中点，a＝8，eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))＝8，
∴eq \(AD,\s\up6(→))＝eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))，
eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))＝bccs A＝eq \f(1,2)bc＝8，
∴eq \(AD,\s\up6(→))2＝eq \f(1,4)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))2
＝eq \f(1,4)(eq \(AB,\s\up6(→))2＋2eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))＋eq \(AC,\s\up6(→))2)
＝eq \f(1,4)(c2＋2×8＋b2)，
又b2＋c2－a2＝bc，bc＝16，a＝8，
∴b2＋c2＝a2＋bc＝64＋16＝80，
∴eq \(AD,\s\up6(→))2＝eq \f(1,4)(c2＋2×8＋b2)
＝eq \f(1,4)(80＋16)＝24，
即|eq \(AD,\s\up6(→))|＝2eq \r(6)，∴中线AD的长度为2eq \r(6).
(2)∵E为边BC上一点，BE∶EC＝2c∶b，
∴eq \(BE,\s\up6(→))＝eq \f(2c,2c＋b)eq \(BC,\s\up6(→))，
∴eq \(AE,\s\up6(→))－eq \(AB,\s\up6(→))＝eq \f(2c,2c＋b)(eq \(AC,\s\up6(→))－eq \(AB,\s\up6(→)))，
∴eq \(AE,\s\up6(→))＝eq \f(2c,2c＋b)eq \(AC,\s\up6(→))＋eq \f(b,2c＋b)eq \(AB,\s\up6(→))，
即(2c＋b)eq \(AE,\s\up6(→))＝2ceq \(AC,\s\up6(→))＋beq \(AB,\s\up6(→))，
∴(2c＋b)2eq \(AE,\s\up6(→))2＝(2ceq \(AC,\s\up6(→))＋beq \(AB,\s\up6(→)))2，
又AE＝1，∴(2c＋b)2＝(2ceq \(AC,\s\up6(→))＋beq \(AB,\s\up6(→)))2
＝4c2b2＋2b2c2＋b2c2＝7b2c2，
∴2c＋b＝eq \r(7)bc，即eq \f(2,b)＋eq \f(1,c)＝eq \r(7)，
∴2b＋c＝eq \f(1,\r(7))(2b＋c)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,b)＋\f(1,c)))
＝eq \f(1,\r(7))eq \b\lc\(\rc\)(\a\vs4\al\c1(4＋1＋\f(2b,c)＋\f(2c,b)))≥
eq \f(1,\r(7))eq \b\lc\(\rc\)(\a\vs4\al\c1(5＋2\r(\f(2b,c)·\f(2c,b))))＝eq \f(9\r(7),7)，
当且仅当eq \f(2b,c)＝eq \f(2c,b)，
即b＝c＝eq \f(3\r(7),7)时取等号，
故2b＋c的最小值为eq \f(9\r(7),7).
题号
1
2
3
4
5
6
7
8
9
10
11
答案