抽象函数问题课件-2025届高三数学二轮复习

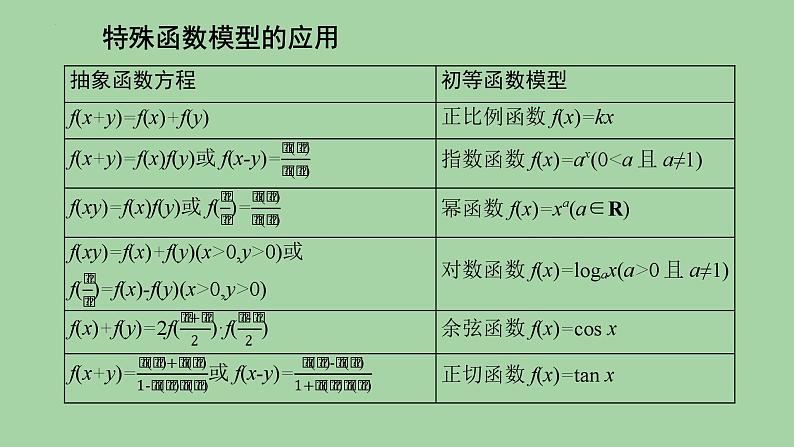
这是一份抽象函数问题课件-2025届高三数学二轮复习，共31页。PPT课件主要包含了赋值法的应用，ABC，特殊函数模型的应用，ABD，ACD，D正确故选D等内容，欢迎下载使用。
抽象函数是指没有具体地给出解析式,只给出它的一些特征或性质的函数;抽象函数型综合问题,一般通过对函数性质的代数表述,综合考查学生对于数学符号语言的理解和接受能力,考查对于函数性质的代数推理和论证能力,考查学生对于一般和特殊关系的认识,是考查学生能力的较好途径.抽象函数问题既是高考的难点,又是近几年高考的热点.
例1(1)(多选题)(2023新高考Ⅰ,11)已知函数f(x)的定义域为R, f(xy)=y2f(x)+x2f(y),则(　　)A.f(0)=0B.f(1)=0C.f(x)是偶函数D.x=0为f(x)的极小值点
解析 对于选项A,令x=0,y=0,f(0)=0,所以A正确;对于选项B,令x=1,y=1,f(1×1)=12×f(1)+12×f(1)=2f(1),解得f(1)=0,所以B正确;对于选项C,令x=-1,y=-1,f[(-1)×(-1)]=(-1)2×f(-1)+(-1)2×f(-1)=2f(-1),解得f(-1)=0;再令x=-1,y=x,f[(-1)×x]=x2×f(-1)+(-1)2×f(x),f(-x)=f(x),所以C正确;对于选项D,用特值法,函数f(x)=0,为常数函数,且满足f(xy)=y2f(x)+x2f(y),而常数函数没有极值点,所以D错误.故选ABC.
(2)(2024辽宁抚顺一模)已知定义域为{x|x≠0}的函数f(x)满足对任意x≠0,y≠0,有f(x+y)[f(x)+f(y)]=f(x)f(y),f(1)=2,且当x∈(0,+∞)时,f(x)>0恒成立,则下列结论正确的是(　　)A.f( )=6B.f(2x)=2f(x)C.f(x)为奇函数D.f(x)在区间(0,+∞)是单调递增函数
假设存在x0时,f(x)>0,所以产生矛盾,即xf(2)=1,故D错误.故选C.
(2)(2024吉林模拟)已知函数f(x)的定义域为R,且f(x+y)+f(x-y)=2f(x)f(y), f(0)=1,f(3x+1)=-f(-3x+1),则 f(k)=(　　)A.-2B.-1C.0D.1
解析(方法一)令x=0,由f(x+y)+f(x-y)=2f(x)f(y),f(0)=1,可得f(-y)=f(y),所以f(x)是偶函数.因为f(3x+1)=-f(-3x+1),所以函数f(x)的图象关于点(1,0)对称,(方法二)由题意知函数f(x)的定义域为R,且f(x+y)+f(x-y)=2f(x)·f(y),f(0)=1,令x=0,则f(y)+f(-y)=2f(y),即f(-y)=f(y),故f(x)为偶函数;又f(3x+1)=-f(-3x+1),令x=0,则f(1)=-f(1),所以f(1)=0,又由f(3x+1)=-f(-3x+1),得f(x+1)+f(-x+1)=0,即f(x)的图象关于点(1,0)成中心对称,则f(2)=-f(0)=-1.
f(x+1)+f(-x+1)=0,即f(x+2)=-f(-x),又结合f(x)为偶函数,则f(x+2)=-f(x),故f(x+4)=-f(x+2)=f(x),即4为f(x)的周期,故f(3)=f(-1)=f(1)=0,f(4)=f(0)=1,故 f(k)=f(0)+[f(1)+f(2)+…+f(2 024)]=1+506×[f(1)+f(2)+f(3)+f(4)]=1+506×(0-1+0+1)=1,故选D.
抽象函数性质的综合应用
例3(1)(多选题)(2024山东聊城一模)设f(x)是定义在R上的可导函数,其导数为g(x),若f(3x+1)是奇函数,且对于任意的x∈R,f(4-x)=f(x),则对于任意的k∈Z,下列说法正确的是(　　)A.4k都是g(x)的周期B.曲线y=g(x)关于点(2k,0)对称C.曲线y=g(x)关于直线x=2k+1对称D.g(x+4k)是偶函数
解析 由f(3x+1)是奇函数,故有f(3x+1)=-f(-3x+1),即有f(x+1)=-f(-x+1),故f'(x+1)=f'(-x+1),即g(x+1)=g(-x+1),故函数g(x)的图象关于直线x=1对称,由f(4-x)=f(x),则-f'(4-x)=f'(x),即-g(4-x)=g(x).故函数g(x)的图象关于(2,0)中心对称.由-g(4-x)=g(x),则-g(3-x)=g(x+1),又g(x+1)=g(-x+1),故g(-x+1)=-g(3-x),即有g(x+1)=-g(3+x),则g(x+3)=-g(x+5),故g(x+3)=-g(x+5)=-g(x+1),即g(x+1)=g(x+5),故g(x)=g(x+4),故g(x)的周期为4.对于A,当k=0时,4k=0,故A错误;
对于B,由g(x)周期为4,故g(4k-x)=g(-x),又-g(4-x)=g(x),故-g(-x)=g(x),故g(-x)=-g(x)=g(4k-x),故曲线y=g(x)关于点(2k,0)对称,故B正确;对于C,由g(x)的周期为4,故g(4k+2-x)=g(2-x),又g(x+1)=g(-x+1),故g(x)=g(-x+2)=g(4k+2-x),故曲线y=g(x)关于直线x=2k+1对称,故C正确;对于D,由选项B得-g(x)=g(4k-x),故-g(-x)=g(4k+x),又g(x)的周期为4,故有-g(-x)=-g(4k-x),故g(4k+x)=-g(4k-x),又x∈R,即g(x+4k)都是奇函数,故D错误.故选BC.
(2)(多选题)(2024山东青岛期末)已知函数f(x)及其导函数f'(x)的定义域均为R,若f(x)是奇函数,f(2)=-f(1)≠0,且对任意x,y∈R,f(x+y)=f(x)f'(y)+f'(x)f(y),则(　　)
解析 因为f(x+y)=f(x)f'(y)+f'(x)f(y),令x=y=1,得f(2)=2f(1)f'(1),又因为f(2)=-f(1)≠0,所以f'(1)=- ,故A正确;因为f(x)是定义域为R的奇函数,所以f(0)=0,且f'(x)为偶函数.令y=1,可得f(x+1)=f(x)f'(1)+f'(x)f(1).①再用-x代替x,可得f(1-x)=f(-x)·f'(1)+f'(-x)f(1)=-f(x)f'(1)+f'(x)f(1),则f(x-1)=f(x)f'(1)-f'(x)f(1).②①+②,得f(x+1)+f(x-1)=2f(x)·f'(1),则f(x+1)=-f(x)-f(x-1),所以f(x+2)=-f(x+1)-f(x),f(x+3)=-f(x+2)-f(x+1)=f(x+1)+f(x)-f(x+1)=f(x),所以f(x)是周期为3的周期函数,所以f(6)=f(3)=f(0)=0,故B正确;
针对训练1.(多选题)(2024安徽安庆二模)已知定义在R上的函数f(x),满足对任意的实数x,y,均有f(x+y)=f(x)+f(y)-1,且当x>0时,f(x)0时,f(x)0,则有f(x+y)-f(x)=f(y)-1,其中x+y>x,f(y)-1x2时,f(x1)-f(x2)