山东省日照市岚山区2024-2025学年九年级上学期期中考试数学试题

这是一份山东省日照市岚山区2024-2025学年九年级上学期期中考试数学试题，文件包含教研室提供山东省日照市岚山区2024-2025学年九年级上学期期中考试数学试题docx、九年级数学答案docx等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。
（满分：120分 时间：120分钟）
一、选择题：（本题共12个小题，每小题3分，满分36分．在每小题给出的四个选项中，有一项是符合题目要求的，请将符合题目要求选项的字母代号填涂在答题卡相应位置上）
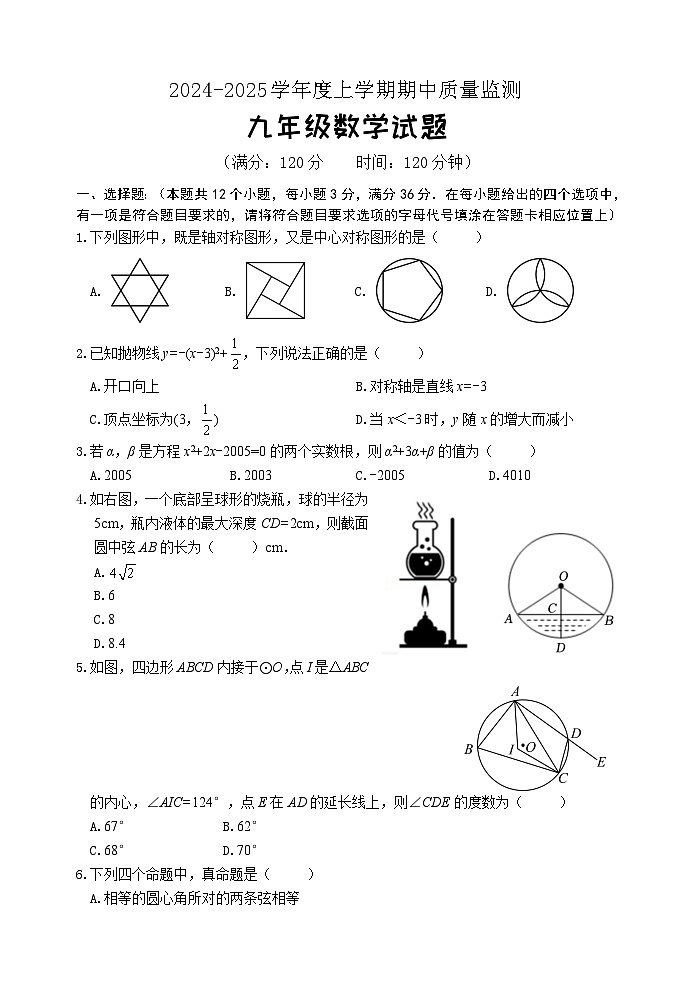
1.下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A. B. C. D.
2.已知抛物线y=-(x-3)2+，下列说法正确的是（ ）
A.开口向上 B.对称轴是直线x=-3
C.顶点坐标为(3，) D.当x＜-3时，y随x的增大而减小
3.若α，β是方程x2+2x-2005=0的两个实数根，则α2+3α+β的值为（ ）
A.2005 B.2003 C.-2005 D.4010
4.如右图，一个底部呈球形的烧瓶，球的半径为5cm，瓶内液体的最大深度CD=2cm，则截面圆中弦AB的长为（ ）cm．
A.
B.6
C.8
D.8.4
5.如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC=124°，点E在AD的延长线上，则∠CDE的度数为（ ）
A.67° B.62°
C.68° D.70°
6.下列四个命题中，真命题是（ ）
A.相等的圆心角所对的两条弦相等
B.平分弦的直径一定垂直于这条弦
C.三角形的内心是到三角形三边距离相等的点
D.等弧就是长度相等的弧
7.如图，将△ABC绕点C按逆时针方向旋转至△DEC，
使点D落在BC的延长线上，已知∠A=30°，
∠B=35°，则∠BCE的大小是（ ）
A.30° B.35°
C.45° D.65°
8.近两年某县县委、县政府将课后服务列入为民办实事项目，全县多所小学、初中课服务全面启动．预计两年后参与课后服务学生可由最初的2万人增加至2.88万人，如果每年的平均增长率相同，那么这两年课后服务人数的平均增长率为（ ）
% B.10% C.14.4% D.20%
9.函数y=ax2-x+2和y=-ax-a(a≠0)在同一平面直角坐标系中的图象可能是（ ）

A B C D
10.如图，DE与⊙O相切于点D，交直径AB的
延长线于点E，C为圆上一点，∠ACD=60°．
若DE的长度为3，则BE的长度为（ ）．
A. B.
C. D.2
11.如图，在▱ABCD中，∠A=60°，AB=2，AD=1，点E，F在▱ABCD的边上，从点A同时出发，分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动，到达点C时停止，线段EF扫过区域的面积记为y，运动时间记为x，能大致反映y与x之间函数关系的图象是（ ）

A B C D
12.如图是抛物线y=ax2+bx+c(a＜0)的部分图象，其顶点坐标为(1，n)，且与x轴的一个交点在点(3，0)和(4，0)之间，则下列结论：①a-b+c＞0；②3a+b=0；③b2=4a(c-n)；④一元二次方程ax2+bx+c=n-1无实数根；⑤a+b≥am2+bm
(m为任意实数)；其中正确结论的个数是（ ）
A.1个 B.2个 C.3个 D.4个
二、填空题（本大题共4个小题，每小题4分，共16分．不需写解答过程，请将答案直接写在答题卡相应位置上）
13.已知二次函数y=-x2+4x+5，若-3≤x≤8，则y的取值范围是 ．
14.关于x的一元二次方程x2-kx+2k-1=0有两个实数根分别为x1，x2，且两个根的平方和为7，则k= ．
15.二次函数y=ax2+bx+c(a，b，c是常数，a≠0)的自变量x与函数值y的部分对应值
如表：
且当x=时，与其对应的函数值y＞0，有下列结论：①函数图象的顶点在第四象限内；②-2和3是关于x的方程ax2+bx+c＝t的两个根；③0＜m+n＜，④若点(-8，y1)，
点(8，y2)在二次函数图象上，则y1＜y2；⑤方程ax2+bx+c+＝0有两个不相等的实数根．其中，正确的结论是 ．（把所有正确结论的序号都填上）
16.如图，P是正方形ABCD内一点，PA=2，PB=3，PD=1，将线段PA以点A为旋转中心逆时针旋转90°得到线段APʹ，连接DPʹ．下列结论：
①△APʹD可以由△APB绕点A逆时针旋转90°得到；
②点P与Pʹ的距离为2；
③∠APD=135°；
④S正方形ABCD=5+；
⑤S△APB=2+．
其中正确的结论是 ．（填序号）
三、解答题（本大题共6小题，满分68分．解答要写出必要的文字说明，证明过程或演算步骤）
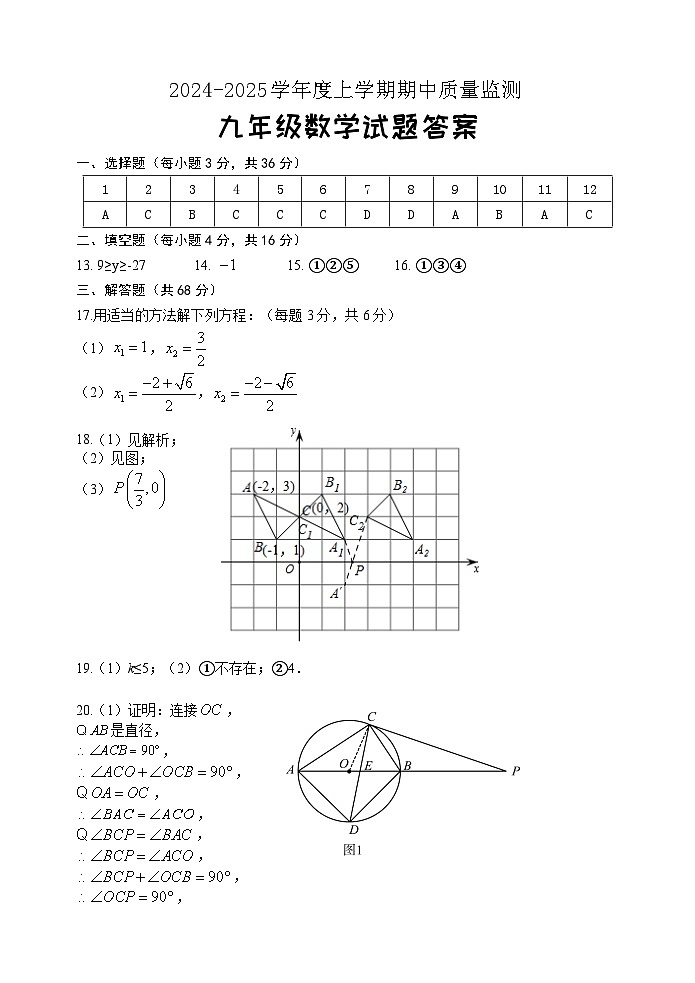
17.（6分）解下列方程：
（1）；
（2）．
18.（10分）△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC关于点C成中心对称的△A1B1C1．
（2）将△A1B1C1向右平移个单位，作出平移后的△A2B2C2．
（3）在x轴上求作一点P，使PA1+PC2的值最小，并求出点P的坐标．
19.（12分）关于x的一元二次方程x2-4x+k-1=0有两个实数根x1、x2．
（1）求k的取值范围；
（2）若x1、x2分别是一个矩形的长和宽．
①是否存在k，使得矩形的面积为10，若存在，请求出k的值；若不存在，请说明理由；
②是否存在k，使得矩形的对角线长为？若存在，请求出k的值；若不存在，请说明理由.
20.（12分）如图，AB是⊙O的直径，AC是弦，∠BCP=∠BAC，∠ACB的平分线交⊙O于点D．
（1）求证：PC是的切线；
（2）求证：△PEC是等腰三角形；
（3）若AC+BC=时，求CD的长.添加适当的辅助线，是解题的关键．
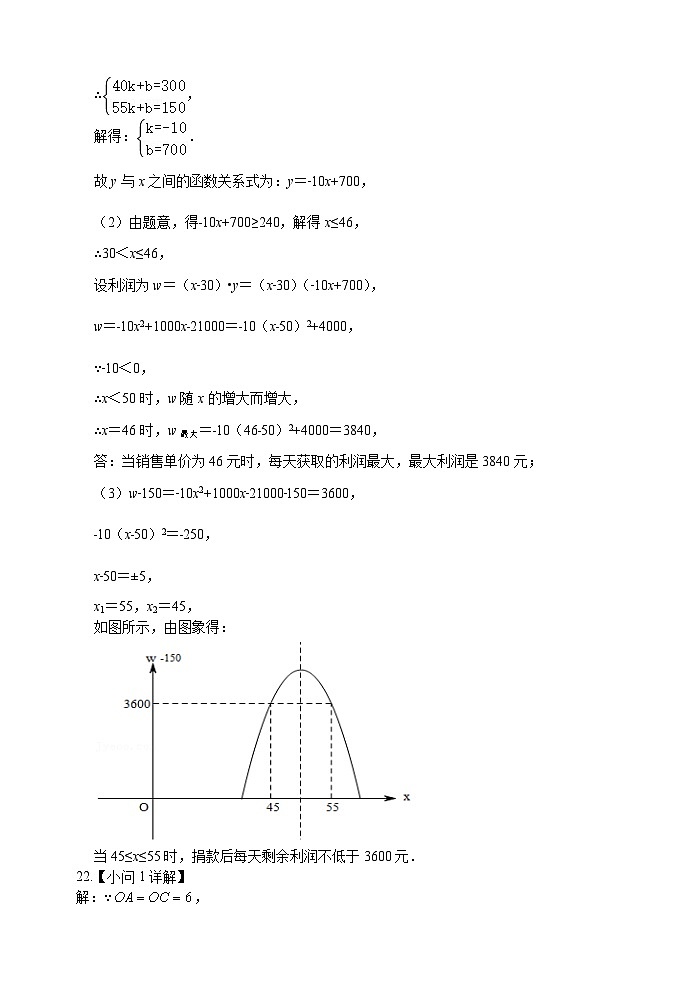
21．（12分）“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图所示．
（1）求y与x之间的函数关系式；
（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？
（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围．
22.（16分）如图，抛物线与x轴交于A，B两点，与y轴交于点C，OA=OC=6，对称轴是x=-2，点F在对称轴上运动．
（1）求抛物线的解析式；
（2）是否存在一点F，使得∠BFC为直角？若存在，求点F的坐标；若不存在，请说明理由；
（3）在直线AC上方抛物线找一点P，使△PAC面积最大，求出点P和面积最大值；
（4）将线段BC绕着点F逆时针方向旋转90°后得到线段B1C1，当点B1与C1恰有一点落在抛物线上时，直接写出点F的坐标．
x
…
-2
-1
0
1
2
…
y=ax2+bx+c
…
t
m
-2
-2
n
…