河北省邯郸市汉光中学2024-2025学年八年级上学期第一次月考数学试卷（原卷版）-A4

这是一份河北省邯郸市汉光中学2024-2025学年八年级上学期第一次月考数学试卷（原卷版）-A4，共7页。
A. B.
C. D.
2. 一个三角形三边长分别为2，5，x，另一个三角形的三边长分别为y，2，6，若这两个三角形全等，则x+y=（ ）
A. 11B. 7C. 8D. 13
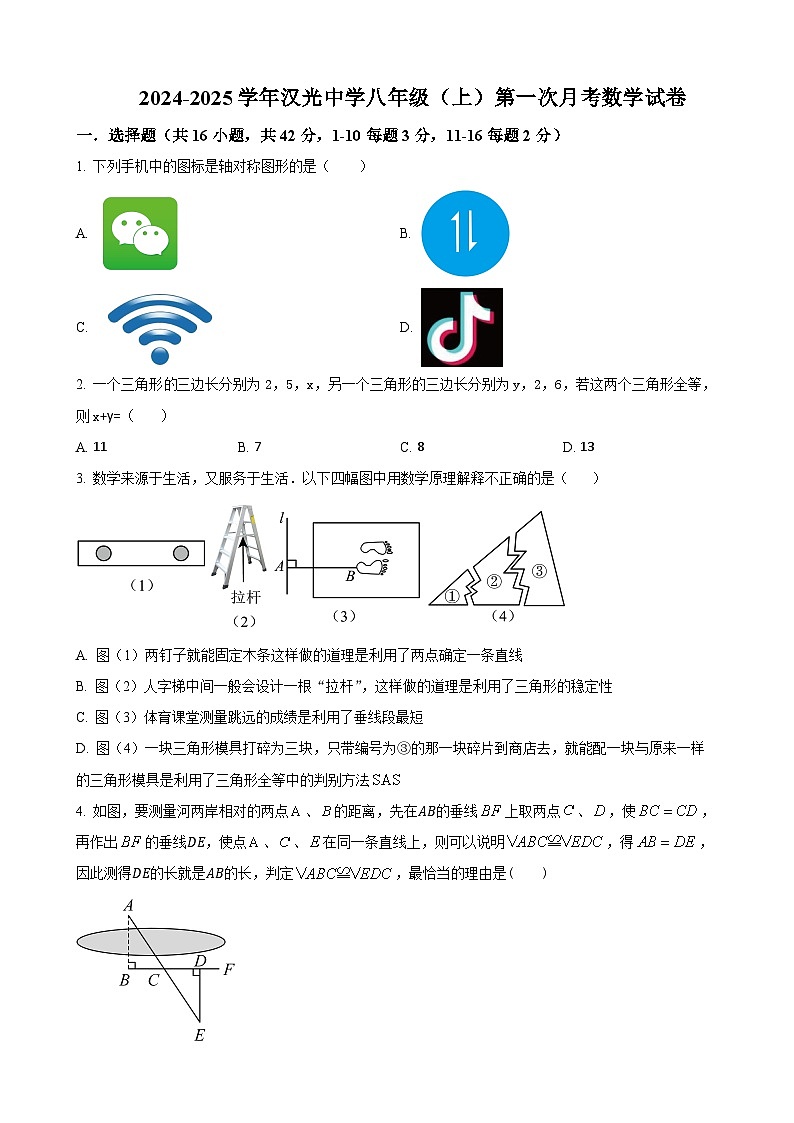
3. 数学来源于生活，又服务于生活．以下四幅图中用数学原理解释不正确的是（ ）
A. 图（1）两钉子就能固定木条这样做的道理是利用了两点确定一条直线
B. 图（2）人字梯中间一般会设计一根“拉杆”，这样做的道理是利用了三角形的稳定性
C. 图（3）体育课堂测量跳远的成绩是利用了垂线段最短
D. 图（4）一块三角形模具打碎为三块，只带编号为③的那一块碎片到商店去，就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法
4. 如图，要测量河两岸相对的两点、的距离，先在AB的垂线上取两点、，使，再作出的垂线DE，使点、、在同一条直线上，则可以说明，得，因此测得DE的长就是AB的长，判定，最恰当的理由是( )
A. B. C. D.
5. 如图，已知方格纸中是4个相同的正方形，则∠1+∠2+∠3的度数为（ ）

A. 90°B. 105°C. 120°D. 135°
6. 如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是( )
A. AD=FBB. DE=BDC. BF=DBD. 以上都不对
7. 如图，正方形的边长为，则图中阴影部分面积为（ ）
A. B. C. D.
8. 如图，若AB⊥BD，CD⊥BD，AD＝BC，则判定△ABD和△CDB全等的依据是（ ）
A. A•A•SB. S•A•SC. A•S•AD. H•L
9. 如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，再分别以点为圆心，大于的长为半径画弧，两弧交于点，作射线交边于点，若，，则的面积是（ ）

A. 15B. 30C. 45D. 60
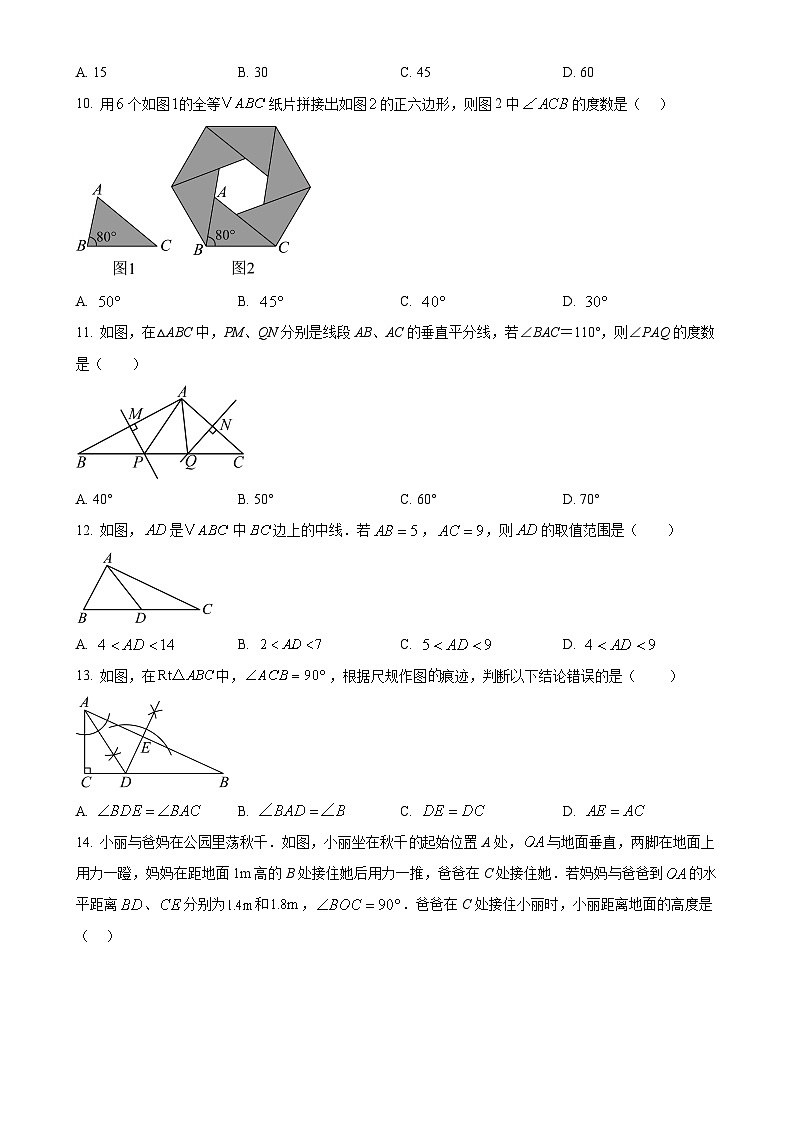
10. 用个如图的全等纸片拼接出如图的正六边形，则图2中的度数是（ ）
A. B. C. D.
11. 如图，在△ABC中，PM、QN分别是线段AB、AC的垂直平分线，若∠BAC＝110°，则∠PAQ的度数是（ ）

A. 40°B. 50°C. 60°D. 70°
12. 如图，是中边上的中线．若，，则的取值范围是（ ）
A. B. C. D.
13. 如图，在中，，根据尺规作图痕迹，判断以下结论错误的是（ ）
A. B. C. D.
14. 小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千起始位置A处，与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到的水平距离、分别为和，．爸爸在C处接住小丽时，小丽距离地面的高度是（ ）

A. B. C. D.
15. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A. 1个B. 2个C. 3个D. 4个
16. 如图，△ABC中，∠ABC、∠FCA的角平分线BP、CP交于点P，延长BA、BC，PM⊥BE于M，PN⊥BF于N，则下列结论：①AP平分∠EAC；②；③；④．其中正确结论的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
二．填空题（共4小题，共12分，每小题3分）
17. 如图，在中，于点D，若，则=___________．
18. 为了测量一幢层高楼的层高，在旗杆与楼之间选定一点．测得旗杆顶的视线与地面的夹角，测楼顶的视线与地面的夹角，量得点到楼底的距离与旗杆的高度都等于米，量得旗杆与楼之间距离为米，则每层楼的高度大约_____米．
19. 中，，，点D为的中点．如果点P在线段上以2的速度由B点向C点运动，同时，点Q在线段上由C点向A点运动，若点Q的运动速度为，则当与全等时，_____．
20. 如图，在平面直角坐标系中，已知点A(0，3)，B(9，0)，且∠ACB＝90°，CA＝CB，则点C的坐标为________．
三．解答题（共6小题，共66分）
21. 如图，点E，F上，，，且．
（1）与全等吗？请说明理由；
（2）与平行吗？为什么？
22. 已知，如图，∠1＝∠2，∠C＝∠D，BC＝BD，求证：ABD≌EBC．
23. 如图，四边形中，，，点是上一点，于，于，求证：.
24. 如图，，且点B，D，C在一条直线上，点F在AD上，延长CF交AB于点E．
（1）试说明：．
（2）若，，求的长．
25. 如图，在中，，，于点E，于点D．求证：．
26. 【问题背景】
如图①，在四边形中，，E，F分别是上点，且，试探究线段之间的数量关系．
【初步探索】
小亮同学认为：延长到点G，使，连接，先证明，再证明，则可得到之间的数量关系是 ________________．
【探索延伸】
如图②，在四边形中，分别是上的点，，上述结论是否仍然成立？说明理由．
【结论运用】
如图③，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西的A处，舰艇乙在指挥中心南偏东的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/时的速度前进，舰艇乙沿北偏东的方向以80海里/时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为，试求此时两舰艇之间的距离．