
浙江省绍兴市柯桥区联盟学校2024-2025学年八年级上学期10月月考数学试题(原卷版)-A4
展开
这是一份浙江省绍兴市柯桥区联盟学校2024-2025学年八年级上学期10月月考数学试题(原卷版)-A4,共7页。
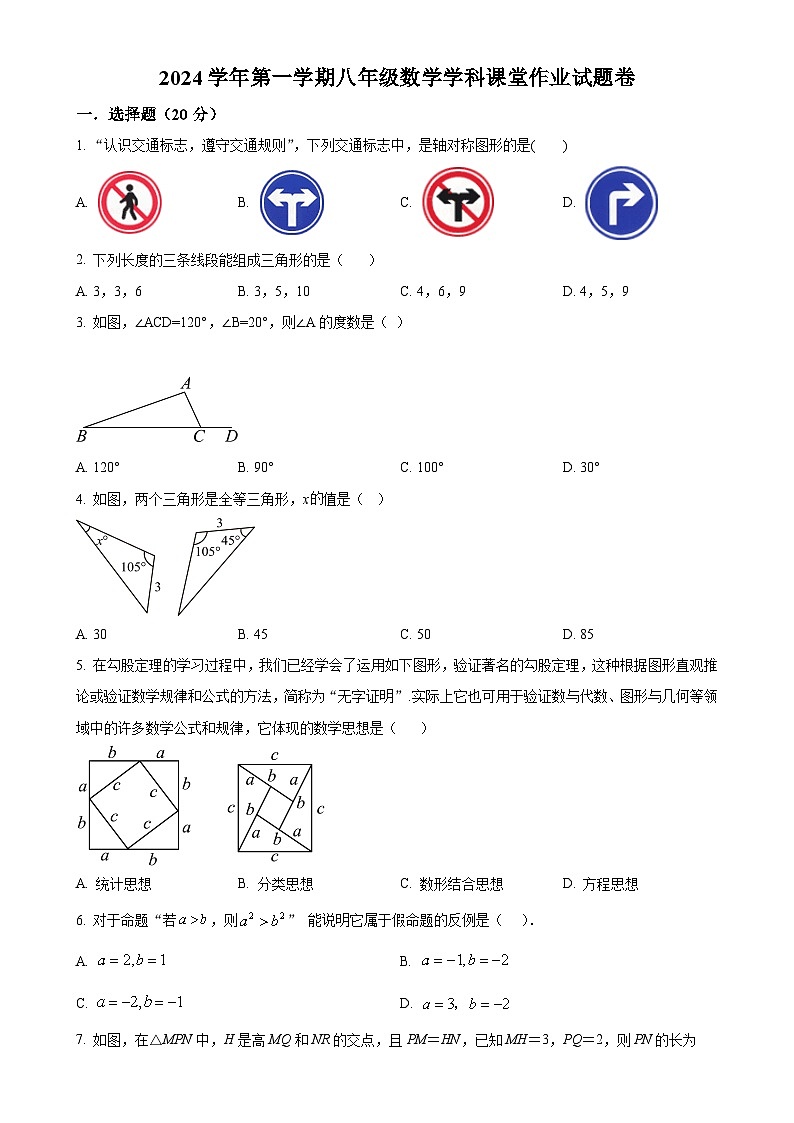
1. “认识交通标志,遵守交通规则”,下列交通标志中,是轴对称图形的是( )
A. B. C. D.
2. 下列长度的三条线段能组成三角形的是( )
A. 3,3,6B. 3,5,10C. 4,6,9D. 4,5,9
3. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A. 120°B. 90°C. 100°D. 30°
4. 如图,两个三角形是全等三角形,x值是( )
A. 30B. 45C. 50D. 85
5. 在勾股定理的学习过程中,我们已经学会了运用如下图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A. 统计思想B. 分类思想C. 数形结合思想D. 方程思想
6. 对于命题“若,则” 能说明它属于假命题的反例是( ).
A. B.
C. D.
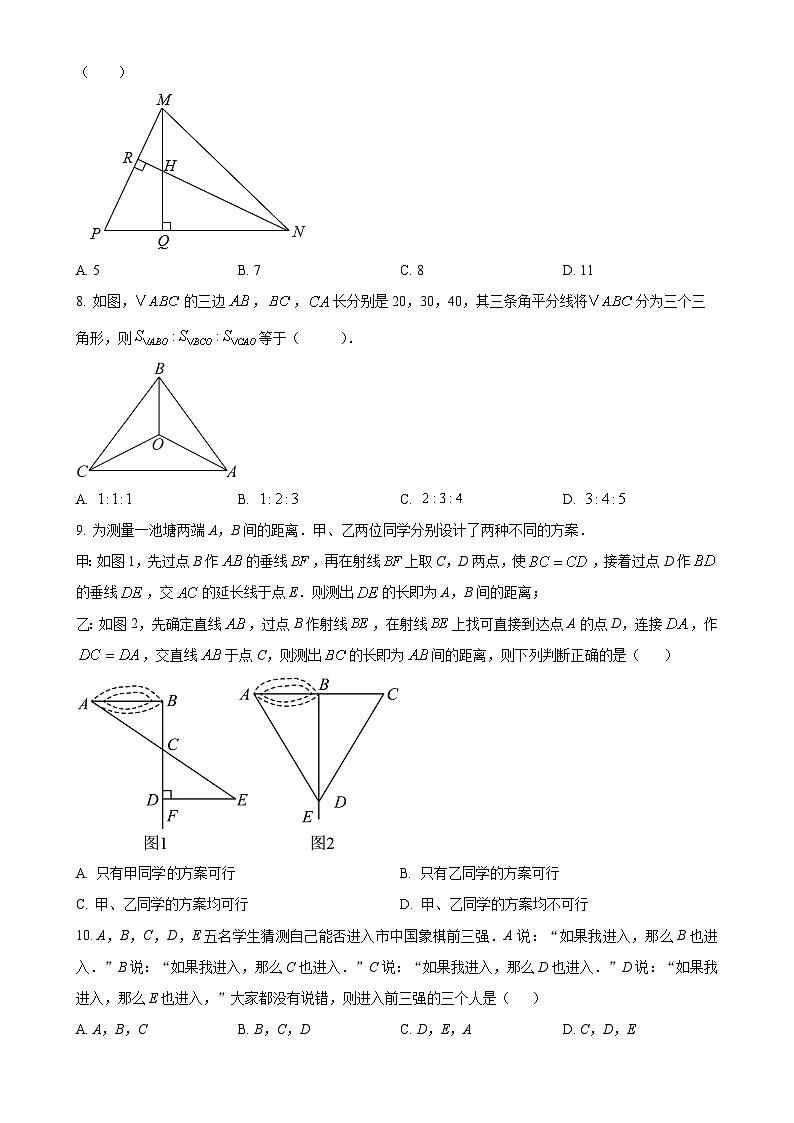
7. 如图,在△MPN中,H是高MQ和NR的交点,且PM=HN,已知MH=3,PQ=2,则PN的长为( )
A. 5B. 7C. 8D. 11
8. 如图,的三边,,长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A. B. C. D.
9. 为测量一池塘两端A,B间的距离.甲、乙两位同学分别设计了两种不同的方案.
甲:如图1,先过点B作的垂线,再在射线上取C,D两点,使,接着过点D作的垂线,交的延长线于点E.则测出的长即为A,B间的距离;
乙:如图2,先确定直线,过点B作射线,在射线上找可直接到达点A的点D,连接,作,交直线于点C,则测出的长即为间的距离,则下列判断正确的是( )
A. 只有甲同学方案可行B. 只有乙同学的方案可行
C. 甲、乙同学的方案均可行D. 甲、乙同学的方案均不可行
10. A,B,C,D,E五名学生猜测自己能否进入市中国象棋前三强.A说:“如果我进入,那么B也进入.”B说:“如果我进入,那么C也进入.”C说:“如果我进入,那么D也进入.”D说:“如果我进入,那么E也进入,”大家都没有说错,则进入前三强的三个人是( )
A. A,B,CB. B,C,DC. D,E,AD. C,D,E
二.填空题(30分)
11. “如果,那么”的逆命题是___________.
12. 如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的_________性.
13. 如图,在的正方形网格中,线段的端点均在格点上,则________.
14. 如图,射线平分,点在射线上,若使,则需添加的一个条件是_________.(只填一个即可)
15. 如图,在和中,,,.若的面积为,则的面积为______.
16. 点在的角平分线上,点到边的距离等于10,点是边上的任意一点,则的取值范围是_____________
17. 如图,在中,,,,则点到边的距离为_________
18. 如图,在中,以点A为圆心,长为半径作圆弧交于点D,再分别以点B和点D为圆心,大于 的长为半径作圆弧,两弧分别交于点M和点N,连接交于点E.若, 则的周长为________________.
19. 在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”,例如:三个内角分别为,,的三角形是“灵动三角形”.如图,,在射线上找一点,过点作交于点,以为端点作射线,交线段于点(规定).当为“灵动三角形”时,则的度数为___.
20. 如图,在中,,,是的平分线,,则面积的最大值为_____.
三.解答题(50分)
21. 如图,的顶点都在方格纸的格点上,按要求在方格纸中画图.
(1)在图①中画出中边上的高线;
(2)在图②中,作直线,将分成面积相等的两个三角形;
(3)在图③中画出一个与全等的.
22. 如图,点B、E、C、F在同一直线上,,
求证:.
23. 如图,在等腰中,,延长到点D,使得,连接,若,求的度数.
24. 下面是多媒体上的一道习题:
请将下面的解题过程补充完整.
25. 如图,在中,,BD分交于点,过点作交于点,,垂足为点.
(1)求证:;
(2)若,,求BD的长.
26. 已知在中,,,点是平面内一点,连接、、,.
(1)如图1,点在的内部.
①当,求的度数;
②当平分,判断的形状,并说明理由;
(2)如果直线与直线相交于点,如果是以为腰的等腰三角形,求的度数(直接写出答案).
27. 在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
如图是中线,,求的取值范围.
解:延长至点E,使,连接.
∵是的中线,
∴ ,
在和中,
,
∴( ),
∴,
在中,根据“三角形三边关系”可知:_____________________,
又∵,
∴______________________.
相关试卷
这是一份浙江省绍兴市柯桥区联盟学校2024-2025学年八年级上学期10月月考数学试题(解析版)-A4,共23页。
这是一份浙江省绍兴市柯桥区柯桥区联盟学校2024~2025学年七年级(上)期中数学试卷(含答案),共5页。
这是一份浙江省绍兴市柯桥区联盟学校2024~2025学年八年级上学期11月期中数学试题(含答案),共12页。





![[数学]浙江省绍兴市柯桥区柯桥区联盟学校2023-2024学年八年级下学期4月期中试题(解析版)](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/2/3/15887234/0-1719023424875/0.jpg?x-oss-process=image/resize,w_202)



