
河南省濮阳市2024-2025学年八年级上学期11月期中考试数学试卷(含答案)
展开
这是一份河南省濮阳市2024-2025学年八年级上学期11月期中考试数学试卷(含答案),共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
一、单选题
1.汉字是世界上最美的文字,形美如画、有的汉字是轴对称图形,下面四个汉字中是轴对称图形的是( )
A.B.C.D.
2.如图,为了估计池塘两岸A,B间的距离,在池塘的一侧选取点P,测得米,米,那么A,B间的距离不可能是( )
A.6米B.米C.27米D.18米
3.若点与关于x轴对称所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
4.如图,铜陵长江大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是( )
A.三角形的不稳定性B.三角形的稳定性
C.四边形的不稳定性D.四边形的稳定性
5.在等腰三角形中,,则的度数不可能为( )
A.B.C.D.
6.将一副三角板按如图所示叠放在一起,则图中的度数是( )
A.B.C.D.
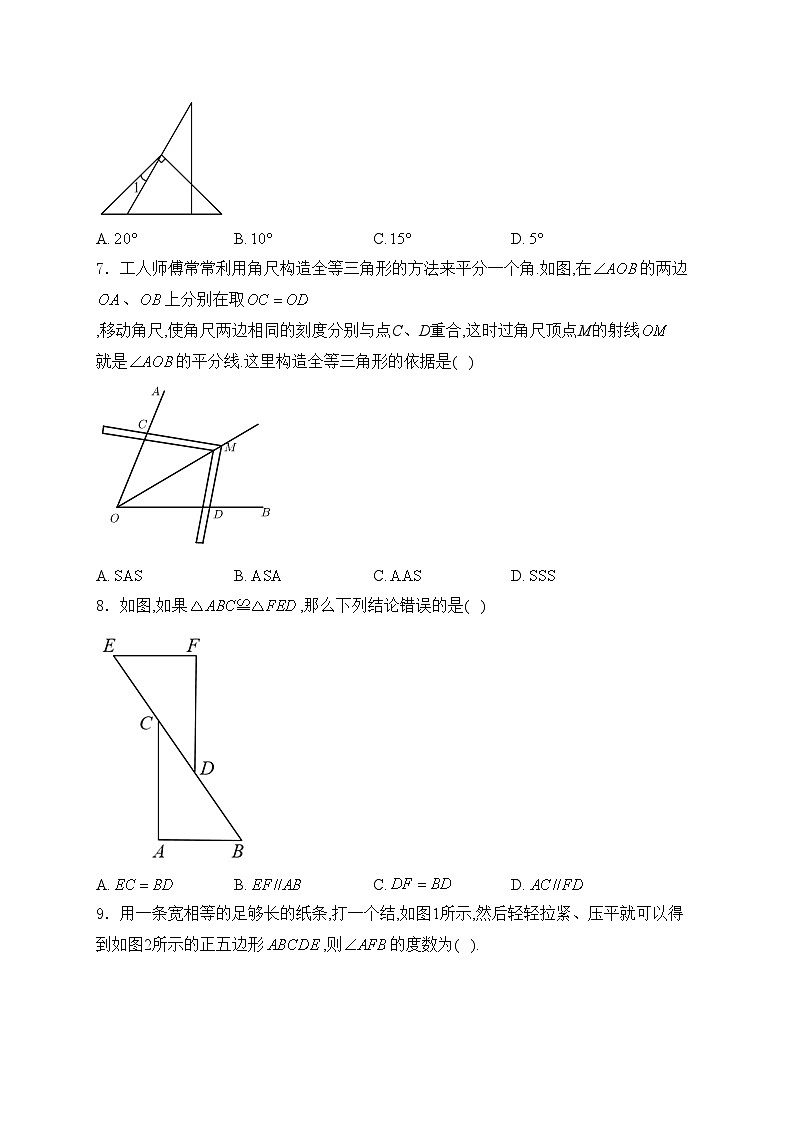
7.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线就是的平分线.这里构造全等三角形的依据是( )
A.B.C.D.
8.如图,如果,那么下列结论错误的是( )
A.B.C.D.
9.用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形,则的度数为( ).
A.B.C.D.
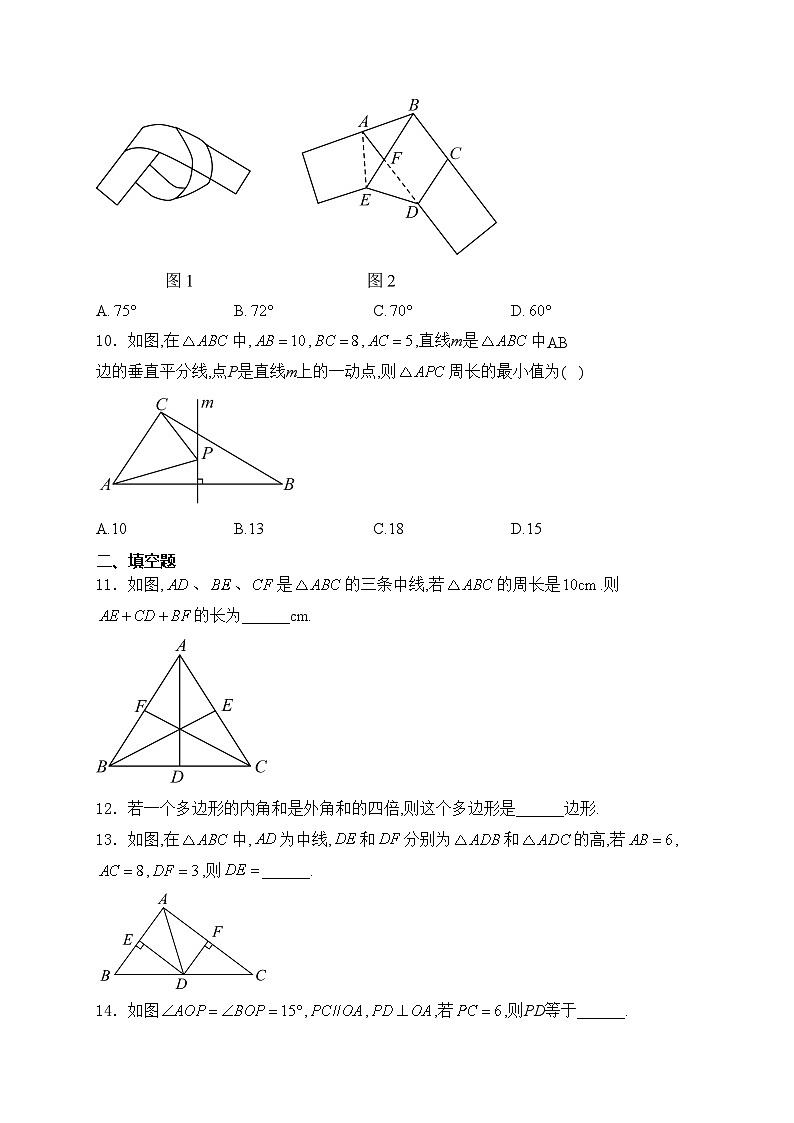
10.如图,在中,,,,直线m是中AB边的垂直平分线,点P是直线m上的一动点,则周长的最小值为( )
A.10B.13C.18D.15
二、填空题
11.如图,、、是的三条中线,若的周长是.则的长为______cm.
12.若一个多边形的内角和是外角和的四倍,则这个多边形是______边形.
13.如图,在中,为中线,和分别为和的高,若,,,则______.
14.如图,,,若,则PD等于______.
15.如图,,垂足为点A,,,射线,垂足为点B,一动点E从A点出发以秒的速度沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,当点E离开点A后,运动______秒时,.
三、解答题
16.已知:如图,点B,F,C,E在一条直线上,,,.求证:.
17.如图,点D、E在的边上,,,求证:.
18.在平面直角坐标系中的位置如图所示.
(1)写出点A,B,C关于y轴的对称点、、的坐标;
(2)作出与关于x轴对称的;
(3)求出的面积.
19.如图,某游乐园有两个长度相等的滑梯与,滑梯的高与滑梯水平方向的长度相等,.国家部门针对滑梯类儿童游乐设备进行了安全范围内的考量,并作出了严格的安全界限:在滑行方向上,要求整体滑行区与水平面的夹角应不大于.请问滑梯与滑梯是否符合国家规定?请说明理由.
20.如图,在中,于点D,平分交于点E,,.
(1)求的度数;
(2)求的度数.
21.(1)如图1,在中,已知点O是内角、的平分线的交点,若,求的度数.
(2)如图2,在中,已知点O是外角、的平分线的交点,若,求的度数(用含有的式子表示).
22.阅读下面材料
【问题情境】
课外兴趣小组活动时,老师提出问题:如图①.在中,若,,求边上的中线取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长到点E,使,请根据小明方法思考:
(1)由已知和作图能得到的理由是_______;
A.B.C.D.
(2)由三角形三边的关系可求得长的取值范围是________;
解后反思:题中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到一个三角形中.
(3)【初步运用】
如图②,是的中线,交于E,交于F,且,若,,求线段的长.
23.如图,在中,,平分于E,点F在边上,连接.
(1)求证:;
(2)若,,,求的长度;
(3)若,,,直接写出BE的长度(用含m,n的代数式表示).
参考答案
1.答案:C
解析:A、不是轴对称图形,不合题意;
B、不是轴对称图形,不合题意;
C、是轴对称图形,符合题意;
D、不是轴对称图形,不合题意;
故选:C.
2.答案:C
解析:设米,
,,
∴由三角形三边关系定理得:
∴,
所以选项C不符合,选项A、B、D符合,
故选:C.
3.答案:D
解析:由点与点关于x轴对称,得
,.
故在第四象限.
故选:D.
4.答案:B
解析:由题中描述可知,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是三角形的稳定性,
故选:B.
5.答案:C
解析:当为顶角时,,则B选项不符合题意;
当为底角、为顶角时时,,则A选项不符合题意;
当、为底角时,,则D选项不符合题意;
综上,选项C符合题意.
故选:C.
6.答案:C
解析:如图,
,
由题意得:,,
∵,
∴,
故选:C.
7.答案:D
解析:由题意可知,,
在和中
∴(SSS)
∴
∴就是的平分线
故选:D.
8.答案:C
解析:∵,
∴,,,,
∴,,,
∴,
∴选项A、B、D都正确,而DF和BD不能确定是否相等,
故选C.
9.答案:B
解析:因为正五边形的每个内角都相等,边长相等,
所以,
∵正五边形的每条边相等,
∴和是等腰三角形,
∴,,
∴.
∴.
故选:B.
10.答案:B
解析:如图所示,连接,
∵直线m是中AB边的垂直平分线
∴,
∵,
∴当点B,P,C三点共线时,,此时线段最小,
∵周长为,是定值,
∴当最小时,周长最小,
∴,
∴周长的最小值为,
故选:B.
11.答案:5
解析:∵、、是的三条中线,
∴,,,
∴,
而的周长是,
∴.
故答案为:5.
12.答案:十
解析:∵一个多边形的内角和是外角和的四倍,
∴这个多边形的内角和为,
设这个多边形的边数为n,则,
解得,即这个多边形是十边形,
故答案为:十.
13.答案:4
解析:∵在中,为中线,
∴,
∵和分别为和的高,
∴,即,
∴,
故答案为:4.
14.答案:3
解析:过P作于E,
∵,,,
∴,,
∵,
∴,
又为直角三角形,且,
∴,.
15.答案:1或3
解析:,,
,
当E在上时,
当时,则,
,
,
E离开点A后,运动的时间为:秒,
当E在上时,
当时,则,
,
,
E离开点A后,运动的时间为:秒,
综上所述:当点E离开点A后,运动1或3秒时,,
故答案为:1或3.
16.答案:证明见解析
解析:证明:∵,
∴,
∴,
在和中,
,
∴.
17.答案:证明见解析
解析:证明:如图,过点A作C于P.
∵,
∴;
∵,
∴,
∴,
∴.
18.答案:(1),,
(2)作图见解析
(3)
解析:(1)根据图示可得,,,,
由点关于轴对称,横坐标变为相反数,纵坐标不变可得,,,;
(2)如图所示,
∴即为所求图形;
(3),
∴的面积为.
19.答案:滑梯符合国家规定,滑梯不符合国家规定,理由见解析
解析:在和中,
,
,
,
.
∵,,
∴滑梯符合国家规定,滑梯不符合国家规定.
20.答案:(1)
(2)
解析:(1)在中,,
∴.
∵是的角平分线,
∴;
(2)∵,
∴,
∴,
∴.
21.答案:(1)
(2)
解析:(1)∵点O是内角、的平分线的交点,
∴,,
∴,
∵,,
∴,
∴,
∵,
∴;
(2)∵平分,平分,
∴,,
∵,,
∴,,
∴,
∵,,
∴,
∵,,
∴.
22.答案:(1)D
(2)
(3)8.
解析:(1)延长到点E,使,
∵是的中线,
∴,
∵,
∴,
故选:D;
(2)∵,
∴,,,
∴,
在中,,即,
∴,
∴;
(3)如图,延长至G,使得,连接,
,
由(1)可得:,
∴,,
∵,
∴,
∵,
∴,
∴.
23.答案:(1)见解析
(2)1
(3)
解析:(1)∵
平分,
,
在和中,
∴,
∴;
(2)∵
∴,
在和中,
,
∴,
∴,
,,
,,
,
故答案为:3;
(3)由(2)证明可得:
,
故答案为.
相关试卷
这是一份河南省濮阳市2024~2025学年七年级(上)期中数学试卷(含答案),共9页。
这是一份河南省濮阳市范县2024~2025学年八年级(上)期中数学试卷(含答案),共10页。
这是一份河南省濮阳市2024-2025学年八年级上学期11月期中考试数学试题,共12页。试卷主要包含了试题卷上不要答题,请用0,7米等内容,欢迎下载使用。









