2024~2025学年江苏省南京市六校高一(上)期中联合调研数学试卷(解析版)

这是一份2024~2025学年江苏省南京市六校高一(上)期中联合调研数学试卷(解析版)，共12页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 已知集合，则与集合A的关系为（ ）
A. B. C. D. 1⫋
【答案】B
【解析】，故，其他选项均错误.
故选：B.
2. 命题：的否定是（ ）
A. B.
C. D.
【答案】B
【解析】由命题否定的概念可知，
命题：的否定是：.
故选：B.
3. 已知命题，若命题是命题的必要条件，则命题可以为（ ）
A. B.
C. D.
【答案】C
【解析】由题意是的充分条件，对照选项，当满足时，必满足.
故选：C.
4. 若，且则下列命题正确的是（ ）
A. B.
C. D. 若，则
【答案】C
【解析】由于
对于A，设则，故A错误；
对于B，设则，故B错误；
对于C，，由于，
则.，则.则，故C正确；
对于D，设，则，故D错误.
故选：C.
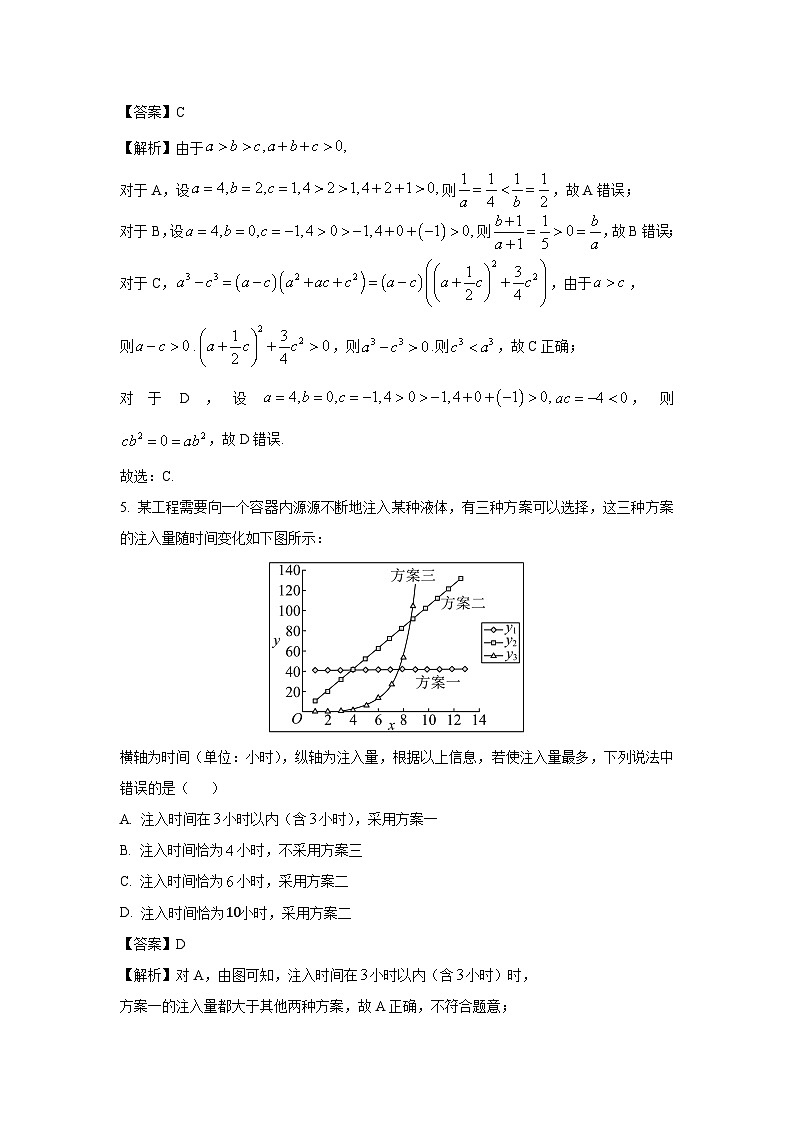
5. 某工程需要向一个容器内源源不断地注入某种液体，有三种方案可以选择，这三种方案的注入量随时间变化如下图所示：
横轴为时间（单位：小时），纵轴为注入量，根据以上信息，若使注入量最多，下列说法中错误的是（ ）
A. 注入时间在小时以内（含小时），采用方案一
B. 注入时间恰为小时，不采用方案三
C. 注入时间恰为小时，采用方案二
D. 注入时间恰为10小时，采用方案二
【答案】D
【解析】对A，由图可知，注入时间在小时以内（含小时）时，
方案一的注入量都大于其他两种方案，故A正确，不符合题意；
对B，当注入时间恰为小时，由图可知，方案三的注入量都小于其他两个方案，
故B正确，不符合题意；
对C，当注入时间恰为小时，方案二的注入量大于其他两个方案，
故C正确，不符合题意；
对D，当注入时间大于8小时，由图可知方案三的注入量最大，故应选择方案三，
D错误，符合题意.
故选：D.
6. 已知，则（ ）
A. B. C. D.
【答案】C
【解析】由得，即，
故，
故，
故.
故选：C.
7. 已知函数，若，则的值为（ ）
A. B. 或C. 或或D. 或或
【答案】B
【解析】依题意，或或，无解，
由解得，则.
由解得，则
故选：B.
8. 已知，若关于的方程恰好有三个互不相等的实根，则实数的取值范围为（ ）
A B.
C. 或D. 或
【答案】D
【解析】记方程的两根为，
当时，恰好有三个互不相等的实根，
等价于与和共有三个不同的交点，
由图可知，此时有，
即，得；
当时，，恰好有三个互不相等的实根，
等价于与有三个不同的交点，
由图可知，此时，即，得.
综上，实数的取值范围为或.
故选：D.
二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对得6分，部分选对得部分分，有选错得0分．
9. 下列命题中为真命题的是（ ）
A. 对任意实数，均有
B. 若，则
C. 设，则“”是“”的必要不充分条件
D. 若，则
【答案】AC
【解析】对于A，因为，所以，故A正确；
对于B，当，时，，，故B不正确；
对于C，当，时，，所以不充分，当时，可知且，
所以必要，故C正确；
对于D，当时，，，
此时，故D不正确.
故选：AC.
10. 如图，已知矩形表示全集，是两个子集，则阴影部分可表示为（ ）
A. B.
C. D.
【答案】AC
【解析】根据图示可知阴影部分表示的元素是属于集合，而不属于集合，
即在阴影部分区域内任取一个元素，则满足，且，即且；
因此阴影部分可表示为，即A正确；
且，因此阴影部分可表示为，C正确；
易知阴影部分表示的集合是和的真子集，即B错误，D错误.
故选：AC.
11. 已知为正实数，且，则（ ）
A. 的最大值为8B. 的最小值为8
C. 的最小值为D. 的最小值为
【答案】ABD
【解析】因为，当且仅当时取等号，
结合，解不等式得，即，故的最大值为8，A正确；
由得，
所以，
当且仅当即时取等号，此时取得最小值8，B正确；
，
当且仅当时取等号，此时取得最小值，C错误；
，
当且仅当即时取等号，
此时取得最小值，D正确.
故选：ABD.
三、填空题：本题共3小题，每小题5分，共15分．
12. 函数的定义域是______．
【答案】
【解析】根据题设可得，故或，
故函数的定义域为：.
13. =______．
【答案】
【解析】
.
14. 已知函数， ，若函数的值域为，则实数的取值范围是______．
【答案】
【解析】，则有，，
由，，所以，
解得，
所以实数的取值范围是.
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15. 已知集合，，，全集，求：
（1）；
（2）；
（3）如果，求的取值范围.
解：（1）依题意，集合，
集合，
所以.
（2）由（1）知，，
所以.
（3）由（1）知，集合，
而或或，
又，因此且，
所以的取值范围是.
16. 已知关于的一元二次不等式的解集为．
（1）求和的值；
（2）求不等式的解集．
解：（1）由题意知和是方程的两个根且，
由根与系数的关系得，解得.
（2）由、，不等式可化为，
即，则该不等式对应方程的实数根为和．
当时，，解得，即不等式的解集为，
当时，，不等式的解集为空集，
当时，，解得，即不等式的解集为，
综上：当时，解集为，
当时，解集为空集，
当时，解集为．
17. 最近南京某地登革热病例快速增长，登革热是一种由登革病毒引起的急性虫媒传染病，主要通过埃及伊蚊和白纹伊蚊传播，为了阻断传染源，南京卫建委在全市范围内组织了蚊虫消杀工作．某工厂针对市场需求开始生产蚊虫消杀工具，经过研究判断生产该工具的年固定成本为50万元，每生产万件，需另外投入成本（万元），，每件工具售价为50元，经过市场调研该厂年内生产的工具能全部销售完．
（1）写出年利润（万元）关于年产量（万件）的函数解析式；
（2）年产量为多少万件时，该厂在这一工具的生产中所获利润最大？
解：（1）当时，，
当时，，
故
（2）时，，
当时，取得最大值，
当时，，
当且仅当即时取到等号，
，时，取得最大值，
18. 已知一次函数和二次函数的图像都过点和，且.
（1）求和的解析式；
（2）设关于的不等式的解集为.
①若，求实数的取值范围；
②是否存在实数，满足：“对于任意正整数，都有；对于任意负整数，都有”，若存在，求出的值，若不存在，说明理由．
解：（1）设，由得，所以；
由题意设 由 得；
又因为，所以，得；
所以，所以.
（2）①原不等式化为恒成立.
（ⅰ）当时，解得，或，
当时，不等式化为，时，解集为；
当时，不等式化为，对任意实数不等式不成立；
（ⅱ）当时，则；
综上所述，实数k的取值范围为．
②根据题意，得出解集，，
当时，解得，或，
时，不等式的解集为，满足条件，
时，恒成立，不满足条件，
当时，此时对应的一元二次不等式的解集形式不是的形式，
不满足条件，
当时，此时对应的一元二次不等式的解集形式不是的形式，
不满足条件，
综上，存在满足条件的的值为．
19. 已知集合，其中，由中元素可构成两个点集和：，，其中中有个元素，中有个元素．新定义1个性质：若对任意的，必有，则称集合具有性质．
（1）已知集合与集合和集合，判断它们是否具有性质，若有，则直接写出其对应的集合，；若无，请说明理由；
（2）集合具有性质，若，求：集合最多有几个元素？
（3）试判断：集合具有性质是的什么条件，并证明．
解：（1）①集合，不符合定义，不具有性质；
②集合具有性质，对应集合，；
③集合不是整数集，所以不具有性质．
（2）依题意，集合的元素构成有序数对，共有个，
由，得，又当时，，则当时，，
因此集合的元素个数不超过个，
取，则中元素的个数为个，
所以中元素的个数最多为.
（3）（i）当集合具有性质时，
①对于，由定义知：，
又集合具有性质，则，
若是中的不同元素，则，中至少有一个不成立，
于是，中至少有一个不成立，
因此也是中不同的元素，
所以的元素个数不多于的元素个数，即，
②对于，由定义知：，
又集合具有性质，则，
若是中的不同元素，则，中至少有一个不成立，
于是，中至少有一个不成立，
因此和也是中不同的元素，
即的元素个数不多于的元素个数，即，
由①②知；
（ii）集合，则，
，满足，而集合不具有性质，
所以集合具有性质是的充分不必要条件.